根据卫星的方位角和仰角画卫星星空图（QT实现）

Posted 2022-11-30 haoming Hu

作者：haomingHu
email：[e-mail]

需求：在0183格式中，根据GNGSV中的卫星仰角和方位角去绘制卫星星空图

如图：

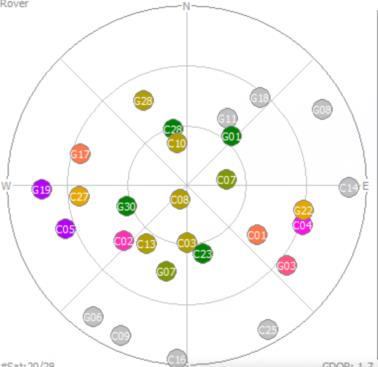
目标：实现一个卫星的映射

名词解释：

方位角：从标准方向的北端起,顺时针方向到直线的水平角称为该直线的方位角。方位角的取值范围为0°～360°。，就是卫星相 对于测量点的方向，正北方向为0 度，顺时针递增。

仰角: 视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角.就是在地平面上，要抬头多少度，才能望到卫星，水平方向为 0 度，头顶的垂直方向为 90 度。

elevation：仰角 、（0-90）azimuth：方位角（0-360）

先用QT画一个圆环

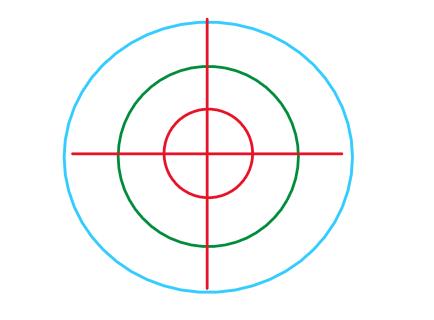
代码如下：

 painter.translate(180,180);//坐标变换  //y轴向下边为正方向
      painter.setRenderHint(QPainter::Antialiasing, true);

      painter.setPen(QPen(QColor("#98F5FF"), 2));
      painter.setBrush(QColor(	255 ,250 ,250));
      painter.drawEllipse(QPointF(0, 0), 180, 180);

      painter.setPen(QPen(QColor("#76EEC6"), 2));
      painter.setBrush(QColor(	255 ,250 ,250));
      painter.drawEllipse(QPointF(0, 0), 120, 120);

      painter.setPen(QPen(QColor("#FFE4B5"), 2));
      painter.setBrush(QColor(	255 ,250 ,250));
      painter.drawEllipse(QPointF(0, 0), 60, 60);

      painter.setPen(QPen(QColor("#696969"), 3));
      painter.drawLine(QPointF(0, 180), QPointF(0,-180));
      painter.drawLine(QPointF(-180,0), QPointF(180,0));

这里需要注意，一定要将坐标原点搬到圆心，否则等下画的卫星就不正确了。坐标平移使用到的函数是：translate
参数为原来坐标系统的圆心坐标，而且平移之后y轴的正方向向下

现在给定参数：

      int elevation =35;
      int azimuth =33;

计算过程：

      int elevation =35;
      int azimuth =33;
      int cosLen = cos(elevation*3.141592/180)*180;
      int y = cos(azimuth*3.141592/180)*cosLen;
      int x = sin(azimuth*3.141592/180)*cosLen;

      qDebug()<< x<<y<<cosLen;
      painter.setPen(QPen(QColor("#FF0000"), 2));
      painter.setBrush(QColor("#FFFAFA"));
      painter.drawEllipse(QPointF(x,-y),10,10);

      painter.setBrush(QColor(255,48,48));
      painter.drawText(QPointF(x-9,-y+5),"13");

最终效果:

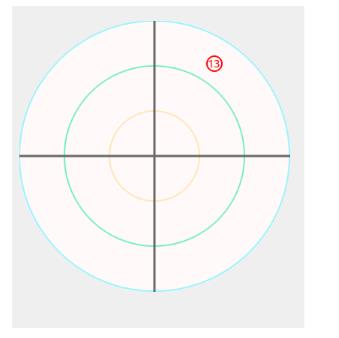
计算过程解释：
int elevation =35;
int azimuth =33;
int cosLen = cos(elevation*3.141592/180)180;
int y = cos(azimuth3.141592/180)cosLen;
int x = sin(azimuth3.141592/180)*cosLen;

  int cosLen = cos(elevation*3.141592/180)*180;  这个是使用仰角计算卫星投射到X-Y平面的点，距离远点的距离

int y = cos(azimuth*3.141592/180)cosLen;
int x = sin(azimuth3.141592/180)*cosLen;
这两个则是用这个距离分别计算投影到X-Y轴的距离。

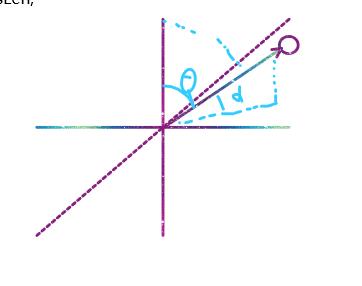
首先假设空间中的卫星和三维坐标系的原点组成一个向量，方位角可以理解为先将这个向量投影到X-Y面，然后得到的新向量与Y轴的夹角，因为三维坐标系绕着X轴转到90°，Z轴和Y轴是重合，所以就可以用正余弦关系计算出最终的二维平面坐标