PyTorch深度学习实战 | 基于多层感知机模型和随机森林模型的某地房价预测
Posted TiAmo zhang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PyTorch深度学习实战 | 基于多层感知机模型和随机森林模型的某地房价预测相关的知识,希望对你有一定的参考价值。

简介: 在现实生活中,除了分类问题外,也存在很多需要预测出具体值的回归问题,例如年龄预测、房价预测、股价预测等。相比分类问题而言,回归问题输出类型为一个连续值,如下表所示为两者的区别。在本文中,将完成房价预测这一回归问题。
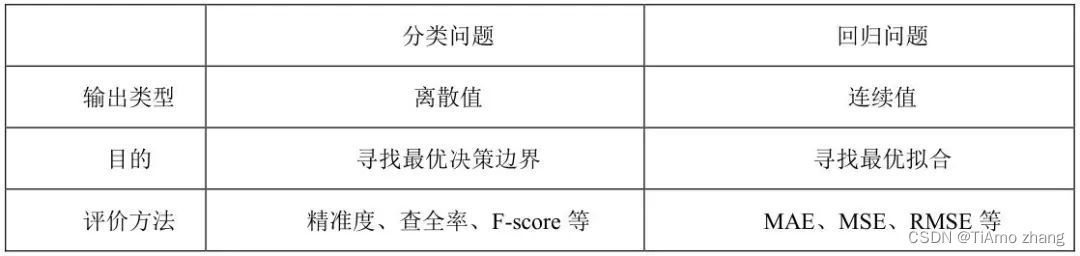
■ 分类问题与回归问题区别
对于一个回归问题,从简单到复杂,可以采取的模型有多层感知机、SVR、回归森林算法等,下面将介绍如何使用这些算法完成这一任务。
01、使用MLP实现房价预测
首先是载入需要的各种包以及数据集,与前面使用树模型等不同的地方在于,使用多层感知机模型需要对数据集的X和y都根据最大最小值进行归一化处理。下图所示程序使用了线性归一化的方法,即

这种归一化方法比较适用在数值比较集中的情况。这种方法有个缺陷,如max和min不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定,实际使用中可以用经验常量值来替代max和min。
sklearn库中提供了归一化的接口,如代码清单1所示为加载数据集并进行归一化处理的代码实现。
代码清单1 加载数据集并进行预处理操作
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error
# 加载数据集并进行归一化预处理
def loadDataSet():
boston_dataset = load_boston()
X = boston_dataset.data
y = boston_dataset.target
y = y.reshape(-1, 1)
# 将数据划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 分别初始化对特征和目标值的标准化器
ss_X, ss_y = preprocessing.MinMaxScaler(), preprocessing.MinMaxScaler()
# 分别对训练和测试数据的特征以及目标值进行标准化处理
X_train, y_train = ss_X.fit_transform(X_train), ss_y.fit_transform(y_train)
X_test, y_test = ss_X.transform(X_test), ss_y.transform(y_test)
y_train, y_test = y_train.reshape(-1, ), y_test.reshape(-1, )
return X_train, X_test, y_train, y_test在预处理过数据集后,构建MLP模型,并设置模型的超参数,并在训练集上训练模型。
代码清单2 训练多层感知机模型
def trainMLP(X_train, y_train):
model_mlp = MLPRegressor(
hidden_layer_sizes=(20, 1), activation='logistic', solver='adam', alpha=0.0001, batch_size='auto',
learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=5000, shuffle=True,
random_state=1, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True,
early_stopping=False, beta_1=0.9, beta_2=0.999, epsilon=1e-08)
model_mlp.fit(X_train, y_train)
return model_mlp如代码清单2所示,该模型的超参数较多,最重要的几个超参数为hidden_layer_sizes(隐藏层神经元个数,在本次实验当中隐藏层分别为5和1),activations(激活函数,可以选择relu、logistic、tanh等),solver(优化方法,即sgd、adam等),以及与优化方法相关的learning_rate(学习率),momentum(动量)等,设置完模型参数后,使用fit函数完成训练过程。
代码清单3 测试模型效果
def test(model, X_test, y_test):
y_pre = model.predict(X_test)
print("The mean root mean square error of MLP-Model is ".format(mean_squared_error(y_test, y_pre)**0.5))
print("The mean squared error of MLP-Model is ".format(mean_squared_error(y_test, y_pre)))
print("The mean absolute error of MLP-Model is ".format(mean_absolute_error(y_test, y_pre)))训练完成后在测试集上验证模型的效果,如代码清单3所示,不同于分类模型有准确率召回率等指标,回归模型验证模型效果通常采用MSE,MAE、RMSE等。
MSE(Mean Squared Error)叫做均方误差

MAE(Mean Absolute Error)为平均绝对误差,是绝对误差的平均值,能更好地反映预测值误差的实际情况

RMSE(Root Mean Square Error)为均方根误差,是用来衡量观测值同真值之间的偏差

以上三项指标的值越小,则表示在测试集上预测的结果与真实结果之间的偏差越小,模型拟合效果越好。
如代码清单4所示,在主函数中依次调用上述函数,完成导入数据集、训练、预测的全过程。
代码清单4 构建main函数
if __name__ == '__main__':
X_train, X_test, y_train, y_test = loadDataSet()
# 训练MLP模型
model = trainMLP(X_train, y_train)
test(model, X_test, y_test)最终可得输出如下图1所示。

图1 MLP模型预测效果
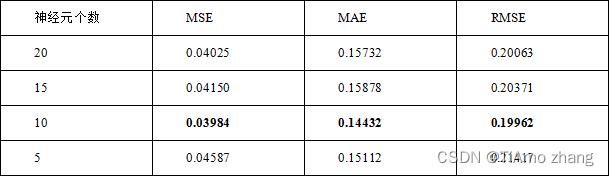
改变实验中的超参数,例如隐藏层的神经元个数,可以得到不同的模型以及这些模型在测试集上的得分。如表2所示,当神经元个数为10时,三项指标均获得了最小值,因此可以固定神经元个数为10,再调整其他参数,例如激活函数、优化方法等。
【小技巧】在难以确定参数时,可以将模型在训练集和测试集的误差都打印出来,当训练集误差远远大于测试集误差时,可能会存在过拟合的问题,应当减少参数数目,即神经元的个数。当训练集的误差与测试集误差都很大时,存在欠拟合的问题,应当增加神经元的个数。
表2 不同神经元个数的预测结果
02、使用随机森林模型实现房价预测
如代码清单5、代码清单6所示,导入与随机森林回归模型有关的包,并新增使用随机森林训练模型的函数,修改主函数,其他部分保持不变。
代码清单5 使用随机森林模型进行训练
def trainRF(X_train, y_train):
model_rf = RandomForestRegressor(n_estimators=10000)
model_rf.fit(X_train, y_train)
return model_rf代码清单6 修改main函数内容
if __name__ == '__main__':
X_train, X_test, y_train, y_test = loadDataSet()
# 训练RF模型
model = trainRF(X_train, y_train)
test(model, X_test, y_test)最终得到如图2所示为命令行输出结果。

图2 随机森林模型预测结果
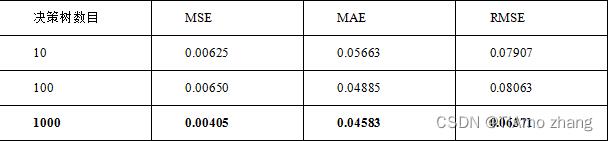
下面调节n_estimators的数目,并记录相应的评价指标大小。如表3所示为一个随机森林中决策数目发生变化时评价指标的变化。可以发现,随着决策树数目的上升,各项指标都变得更优,一般而言,一个森林中决策树的个数越多,模型预测的准确率越高,但相应的会消耗更多的计算资源,因此在实际应用当中应当权衡效率与正确性这两点。
表3 随机森林不同决策树数目预测结果
03、文末赠书
这是一本讲述如何用NLP技术进行文本内容理解的著作,也是一本系统讲解NLP算法的著作,是作者在NLP和内容理解领域多年经验的总结。
本书结合内容理解的实际业务场景,系统全面、循序渐进地讲解了各种NLP算法以及如何用这些算法高效地解决内容理解方面的难题,主要包括如下几个方面的内容:
(1)文本特征表示
文本特征表示是NLP的基石,也是内容理解的基础环节,本书详细讲解了离散型表示方法和分布型表示方法等特征表示方法及其应用场景,还讲解了词向量的评判标准。
(2)内容重复理解
详细讲解了标题重复、段落重复、文章重复的识别方法和去重算法。
(3)内容通顺度识别及纠正
详细讲解了内容通顺度的识别方法以及纠正不通顺内容的各种算法。
(4)内容质量
详细讲解了多种内容质量相关的算法,以及如何搭建高质量的知识问答体系的流程。
(5)标签体系构建
详细讲解了针对内容理解的标签体系的建设流程和方法,以及相关的多种算法。
(6)文本摘要生成
详细讲解了抽取式文本摘要和生成式文本摘要两种流行的文本摘要生成方法,以及文本摘要的常用数据集和文本摘要评价方法。
(7)文本纠错
详细讲解了文本纠错的传统方法、深度学习方法、工业界解决方案,以及常用的文本纠错工具的安装和使用。

◆作者简介◆
李明琦
资深AI技术专家,现就职于BAT,担任高级算法工程师。长期致力于机器学习、深度学习、NLP等技术在实际业务场景中的落地,在内容理解方面有丰富的经验,主导的内容质量项目曾获得最佳项目奖。
先后发表人工智能相关的学术论文2篇,申请人工智能领域的发明专利5项。在GitHub上贡献了大量内容质量、问答系统、NLP等方面的代码,在CSDN撰写了一些与算法、机器学习、内容理解相关的文章,深受欢迎。
谷雪
现为葡萄牙米尼奥大学博士生,涉及的研究领域为神经架构搜索、自然语言处理、情感分析,博士期间着力于细粒度情感原因提取。先后发表过学术论文2篇,其中一篇是神经架构搜索的综述,另一篇是基于进化策略的神经架构演化方法。在开源平台GitHub上贡献了大量深度学习、机器学习代码,在CSDN上分享了服务器配置、数据分析、图像去噪、情感分析等方向的多篇文章。
孟子尧
在人工智能技术领域有非常深厚的积累,擅长机器学习和深度学习,尤其是深度学习中的图像分类和自然语言处理等技术。热衷于开源的应用和推广,在Github和CSDN上贡献了许多代码和文章。曾在《计算机研究与发展》上发表过1篇人工智能相关论文。
参与方式:评论区置顶评论红包手气王自动获得技术图书《基于NLP的内容理解》1本!
深度学习6. 多层感知机及PyTorch实现
深度学习6. 多层感知机及PyTorch实现

一、概念
1. MLP
多层感知机(Multilayer Perceptron)缩写为MLP,也称作前馈神经网络(Feedforward Neural Network)。它是一种基于神经网络的机器学习模型,通过多层非线性变换对输入数据进行高级别的抽象和分类。
与单层感知机相比,MLP有多个隐藏层,每个隐藏层由多个神经元组成,每个神经元通过对上一层的输入进行加权和处理,再通过激活函数进行非线性映射。
MLP的输出层通常是一个 softmax 层,用于多分类任务,或者是一个 sigmoid 层,用于二分类任务。
由于它的强大表达能力和灵活性,MLP被广泛应用于各种机器学习任务中。
2. 前向传播
由于有多个层,参数需要在这些层之间传递。首先需要实现的就是参数的前向传播,计算过程如下:
- 将输入数据传递给第一个隐藏层的神经元;
- 对于每个神经元,计算其加权和,即将输入与对应的权重相乘并求和,再加上偏置项;
- 将加权和输入到激活函数中,得到激活值,作为该神经元的输出;
- 将每个神经元的输出传递到下一层的神经元,直至输出层。
在这个过程中,数据和权重是前向传播的主要传播内容。
3. 反向传播
利用链式法则对网络中的参数进行梯度更新。在训练神经网络时,通常需要定义一个损失函数(loss function),用于评估模型预测结果与真实标签之间的差距。反向传播算法的目标就是最小化这个损失函数。
在反向传播过程中,算法首先计算损失函数对最后一层的输出的梯度,然后根据链式法则逐层向前计算各层的梯度,并利用梯度下降法更新网络中的参数。具体地,算法会先将损失函数对输出的梯度传回网络最后一层,然后依次向前计算各层的梯度。在计算梯度的过程中,算法会利用反向传播公式来计算当前层的梯度,然后将这个梯度传递到前一层。在更新网络参数时,算法会根据计算出的梯度和学习率来更新网络中的权重和偏置。
通过不断地反复迭代前向传播和反向传播两个阶段,可以不断地更新网络中的参数,从而逐渐提高模型的性能。
下面是一个Python计算反向传播的示例:
for epoch in range(num_epochs):
for x, y_true in zip(x_train, y_train):
# 前向传播
hidden_layer = np.maximum(0, np.dot(x, self.weights1) + self.bias1) # ReLU激活函数
y_pred = np.dot(hidden_layer, self.weights2) + self.bias2
# 计算损失和梯度,使用均方误差作为损失函数(Mean Squared Error,MSE)
# 对于每一个样本,模型预测出来的输出与实际输出之间的差异会被平方,
# 然后对所有样本的平方差进行求和并除以样本数,即可得到MSE作为模型的损失函数。
loss = np.square(y_true - y_pred).sum()
# 下面复杂的方法用来实现反向传播
# 计算损失函数关于预测输出的导数
d_loss_pred = -2.0 * (y_true - y_pred)
# 计算输出层的梯度,
d_weights2 = np.dot(hidden_layer.reshape(-1, 1), d_loss_pred.reshape(1, -1))
# 计算输出层偏置的梯度,其值等于输出误差
d_bias2 = d_loss_pred
# 计算隐藏层误差,其中 self.weights2.T 代表输出层权重的转置,
# 计算得到的结果是一个行向量,代表每个隐藏层节点的误差。
d_hidden = np.dot(d_loss_pred, self.weights2.T)
# 将隐藏层误差中小于等于 0 的部分置为 0,相当于计算 ReLU 激活函数的导数,
# 这是因为 ReLU 函数在小于等于 0 的部分导数为 0
d_hidden[hidden_layer <= 0] = 0 # ReLU激活函数的导数
# 计算隐藏层权重的梯度,
# 其中 x.reshape(-1, 1) 代表将输入变为列向量,
# d_hidden.reshape(1, -1) 代表将隐藏层误差变为行向量,
# 两者的点积得到的是一个矩阵,
# 这个矩阵的行表示输入的维度(也就是输入节点的个数),
# 列表示输出的维度(也就是隐藏层节点的个数),表示每个输入和每个隐藏层节点的权重梯度。
d_weights1 = np.dot(x.reshape(-1, 1), d_hidden.reshape(1, -1))
# 计算隐藏层偏置的梯度,其值等于隐藏层误差。
d_bias1 = d_hidden
# 更新权重和偏置
self.weights2 -= learning_rate * d_weights2
self.bias2 -= learning_rate * d_bias2
self.weights1 -= learning_rate * d_weights1
self.bias1 -= learning_rate * d_bias1
4. 评估模式与训练模式
- 在训练阶段,需要调用
model.train()来指定模型为训练模式,以便启用训练中需要的特性,如dropout和batch normalization等。 - 如果在训练过程中需要评估模型的性能,可以在评估前调用
model.eval(),以确保模型处于评估模式,而不是训练模式。 - 在测试阶段,需要调用
model.eval()来指定模型为评估模式,以便禁用dropout和batch normalization等特性,以及启用测试中需要的特性,如在计算中间层的输出等。 - 在预测阶段,需要调用 model.eval() 来指定模型为预测模式,以便禁用
dropout和batch normalization等特性,并且只计算模型的前向传播,以生成模型的输出,而不更新模型的权重。
二、模型定义
1. 加载数据集
本示例使用 MNIST 数据集。
import torch
from torchvision import datasets, transforms
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# 定义ToTensor和Normalize的transform
to_tensor = transforms.ToTensor()
normalize = transforms.Normalize((0.5,), (0.5,))
# 定义Compose的transform
transform = transforms.Compose([
to_tensor, # 转换为张量
normalize # 标准化
])
# 下载数据集
data_train = datasets.MNIST(root="..//data//",
transform=transform,
train=True,
download=True)
data_test = datasets.MNIST(root="..//data//",
transform=transform,
train=False,
download=True)
# 装载数据
data_loader_train = torch.utils.data.DataLoader(dataset=data_train,
batch_size=64,
shuffle=True)
data_loader_test = torch.utils.data.DataLoader(dataset=data_test,
batch_size=64,
shuffle=True)
2. 定义MLP层
下面定义一个有三个层的MLP。
对于这个MLP,它接收一个num_i的输入,输出为num_o的预测值。 隐藏层有2层,每层大小为num_h。
层的定义如下:
- self.linear1:输入层到第一层隐藏层的线性转换,其中num_i为输入的特征数,num_h为第一层隐藏层的特征数。
- self.relu:第一层隐藏层的激活函数,采用ReLU。
- self.linear2:第一层隐藏层到第二层隐藏层的线性转换,其中num_h为第一层隐藏层的特征数,num_h为第二层隐藏层的特征数。
- self.relu2:第二层隐藏层的激活函数,采用ReLU。
- self.linear3:第二层隐藏层到输出层的线性转换,其中num_h为第二层隐藏层的特征数,num_o为输出的特征数(或者说类别数)。
class MLP(torch.nn.Module):
def __init__(self, num_i, num_h, num_o):
super(MLP, self).__init__()
self.linear1 = torch.nn.Linear(num_i, num_h)
self.relu = torch.nn.ReLU()
self.linear2 = torch.nn.Linear(num_h, num_h) # 2个隐层
self.relu2 = torch.nn.ReLU()
self.linear3 = torch.nn.Linear(num_h, num_o)
3. 前向传播
def forward(self, x):
x = self.linear1(x)
x = self.relu(x)
x = self.linear2(x)
x = self.relu2(x)
x = self.linear3(x)
return x
在前向传播时,输入x先通过第一层的线性转换,然后经过第一层隐藏层的激活函数,
再通过第二层的线性转换,再经过第二层隐藏层的激活函数,
最后输出预测值。
4. 优化器
本文将使用PyTorch的优化器工具用于反向传播 。
优化器(optimizer)是一个用于更新模型参数的工具,根据训练集的损失函数(loss function)和反向传播算法(backpropagation algorithm)计算梯度,并使用梯度下降算法(gradient descent algorithm)更新模型参数,以最小化损失函数的值。
PyTorch提供了许多常用的优化器,如随机梯度下降法(SGD)、Adam、Adagrad、RMSprop等。
这些优化器使用不同的更新策略,根据不同的训练任务和数据集选择合适的优化器可以提高训练效率和性能。
5. 反向传播
本文使用和PyTorch优化器的一个实例: torch.optim.Adam(),它使用反向传播算法计算梯度并更新模型的权重,从而调整模型参数以最小化损失函数。
三、训练
def train(model):
cost = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters())
# 设置迭代次数
epochs = 5
for epoch in range(epochs):
sum_loss = 0
train_correct = 0
for data in data_loader_train:
# 获取数据和标签
inputs, labels = data # inputs 维度:[64,1,28,28]
# 将输入数据展平为一维向量
inputs = torch.flatten(inputs, start_dim=1) # 展平数据,转化为[64,784]
# 计算输出
outputs = model(inputs)
# 将梯度清零
optimizer.zero_grad()
# 计算损失函数
loss = cost(outputs, labels)
# 反向传播计算梯度
loss.backward()
# 使用优化器更新模型参数
optimizer.step()
# 返回 outputs 张量每行中的最大值和对应的索引,1表示从行维度中找到最大值
_, id = torch.max(outputs.data, 1)
# 将每个小批次的损失值 loss 累加,用于最后计算平均损失
sum_loss += loss.data
# 计算每个小批次正确分类的图像数量
train_correct += torch.sum(id == labels.data)
print('[%d/%d] loss:%.3f, correct:%.3f%%, time:%s' %
(epoch + 1, epochs, sum_loss / len(data_loader_train),
100 * train_correct / len(data_train),
time.strftime('%Y-%m-%d %H:%M:%S', time.localtime())))
model.eval()
四、测试与预测
# 测试模型
def test(model, test_loader):
test_correct = 0
for data in test_loader:
inputs, lables = data
inputs, lables = Variable(inputs).cpu(), Variable(lables).cpu()
inputs = torch.flatten(inputs, start_dim=1) # 展并数据
outputs = model(inputs)
_, id = torch.max(outputs.data, 1)
test_correct += torch.sum(id == lables.data)
print(f'Accuracy on test set: 100 * test_correct / len(data_test):.3f%')
五、预测
在神经网络模型的推断(inference)阶段中,我们不需要进行反向传播,也不需要计算梯度,使用 with torch.no_grad(): 上下文管理器可以有效地减少内存消耗和计算时间
def predict(model, data):
model.eval()
with torch.no_grad():
output = model(data)
pred = output.data.max(1, keepdim=True)[1]
return pred
output是模型在给定输入数据后的输出结果,每一行对应一个输入数据样本,每一列对应一个可能的输出类别。output.data提取出了output中的数据部分,然后使用max()函数沿着第1个维度(即列)找到每一行中最大的值以及对应的索引。keepdim=True参数使得输出结果保持和输入数据output相同的维度。因此,pred包含每个输入样本的预测类别,是一个包含预测标签索引的一维张量
六、完整代码
import torch
from torchvision import datasets, transforms
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# 定义ToTensor和Normalize的transform
to_tensor = transforms.ToTensor()
normalize = transforms.Normalize((0.5,), (0.5,))
# 定义Compose的transform
transform = transforms.Compose([
to_tensor, # 转换为张量
normalize # 标准化
])
# 下载数据集
data_train = datasets.MNIST(root="..//data//",
transform=transform,
train=True,
download=True)
data_test = datasets.MNIST(root="..//data//",
transform=transform,
train=False,
download=True)
# 装载数据
data_loader_train = torch.utils.data.DataLoader(dataset=data_train,
batch_size=64,
shuffle=True)
data_loader_test = torch.utils.data.DataLoader(dataset=data_test,
batch_size=64,
shuffle=True)
class MLP(torch.nn.Module):
def __init__(self, num_i, num_h, num_o):
super(MLP, self).__init__()
self.linear1 = torch.nn.Linear(num_i, num_h)
self.relu = torch.nn.ReLU()
self.linear2 = torch.nn.Linear(num_h, num_h) # 2个隐层
self.relu2 = torch.nn.ReLU()
self.linear3 = torch.nn.Linear(num_h, num_o)
def forward(self, x):
x = self.linear1(x)
x = self.relu(x)
x = self.linear2(x)
x = self.relu2(x)
x = self.linear3(x)
return x
def train(model):
# 损失函数,它将网络的输出和目标标签进行比较,并计算它们之间的差异。在训练期间,我们尝试最小化损失函数,以使输出与标签更接近
cost = torch.nn.CrossEntropyLoss()
# 优化器的一个实例,用于调整模型参数以最小化损失函数。
# 使用反向传播算法计算梯度并更新模型的权重。在这里,我们使用Adam优化器来优化模型。model.parameters()提供了要优化的参数。
optimizer = torch.optim.Adam(model.parameters())
# 设置迭代次数
epochs = 2
for epoch in range(epochs):
sum_loss = 0
train_correct = 0
for data in data_loader_train:
inputs, labels = data # inputs 维度:[64,1,28,28]
# print(inputs.shape)
inputs = torch.flatten(inputs, start_dim=1) # 展平数据,转化为[64,784]
# print(inputs.shape)
outputs = model(inputs)
optimizer.zero_grad()
loss = cost(outputs, labels)
loss.backward()
optimizer.step()
_, id = torch.max(outputs.data, 1)
sum_loss += loss.data
train_correct += torch.sum(id == labels.data)
print('[%d/%d] loss:%.3f, correct:%.3f%%, time:%s' %
(epoch + 1, epochs, sum_loss / len(data_loader_train),
100 * train_correct / len(data_train),
time.strftime('%Y-%m-%d %H:%M:%S', time.localtime())))
model.train()
# 测试模型
def test(model, test_loader):
model.eval()
test_correct = 0
for data in test_loader:
inputs, lables = data
inputs, lables = Variable(inputs).cpu(), Variable(lables).cpu()
inputs = torch.flatten(inputs, start_dim=1) # 展并数据
outputs = model(inputs)
_, id = torch.max(outputs.data, 1)
test_correct += torch.sum(id == lables.data)
print(f'Accuracy on test set: 100 * test_correct / len(data_test):.3f%')
# 预测模型
def predict(model, data):
model.eval()
with torch.no_grad():
output = model(data)
pred = output.data.max(1, keepdim=True)[1]
return pred
num_i = 28 * 28 # 输入层节点数
num_h = 100 # 隐含层节点数
num_o = 10 # 输出层节点数
batch_size = 64
model = MLP(num_i, num_h, num_o)
train(model)
test(model, data_loader_test)
# 预测图片,这里取测试集前10张图片
for i in range(10):
# 获取测试数据中的第一张图片
test_image = data_test[i][0]
# 展平图片
test_image = test_image.flatten()
# 增加一维作为 batch 维度
test_image = test_image.unsqueeze(0)
# 显示图片
plt.imshow(test_image.view(28, 28), cmap='gray')
plt.show()
pred = predict(model, test_image)
print('Prediction:', pred.item())
以上是关于PyTorch深度学习实战 | 基于多层感知机模型和随机森林模型的某地房价预测的主要内容,如果未能解决你的问题,请参考以下文章