基于支持向量机SVM的脑部肿瘤识别，脑电波样本熵提取

Posted 神经网络机器学习智能算法画图绘图

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于支持向量机SVM的脑部肿瘤识别，脑电波样本熵提取相关的知识，希望对你有一定的参考价值。

目录

支持向量机SVM的详细原理
SVM的定义
SVM理论
Libsvm工具箱详解
简介
参数说明
易错及常见问题
SVM应用实例，基于SVM的的脑部肿瘤识别分类预测
代码
结果分析
展望

支持向量机SVM的详细原理

SVM的定义

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
（1）支持向量机（Support Vector Machine, SVM）是一种对数据进行二分类的广义线性分类器，其分类边界是对学习样本求解的最大间隔超平面。

（2）SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险，是一个具有稀疏性和稳健性的分类器 。

（3）SVM可以通过引入核函数进行非线性分类。

SVM理论

1，线性可分性


2，损失函数

机器学习：基于支持向量机（SVM）进行人脸识别预测

机器学习：基于支持向量机（SVM）进行人脸识别预测

文章目录

一、实验目的

1.理解SVM原理

2.掌握scikit-learn操作SVM的方法

二、实验原理

SVM(Support Vector Machine)指的是支持向量机，是常见的一种判别方法。在机器学习领域，是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

具体原理：
1.在n维空间中找到一个分类超平面，将空间上的点分类。如下图是线性分类的例子。

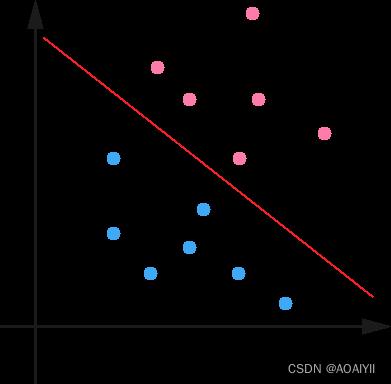
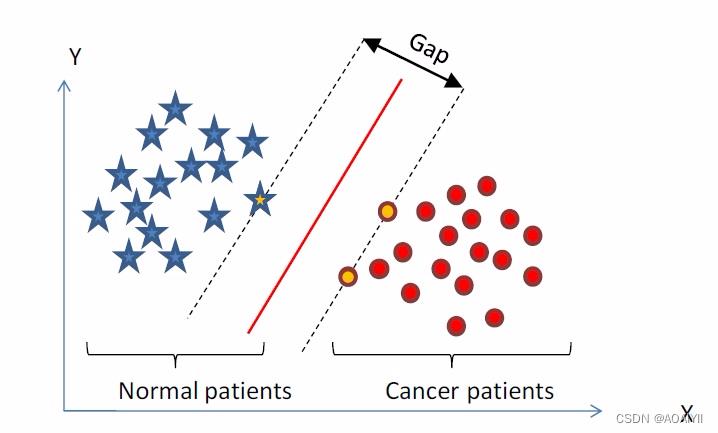
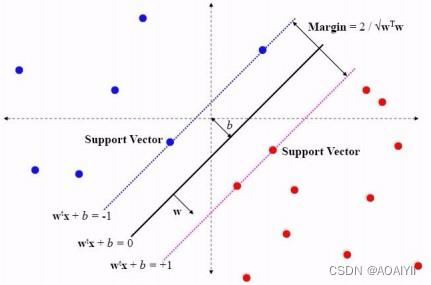
2.一般而言，一个点距离超平面的远近可以表示为分类预测的确信或准确程度。SVM就是要最大化这个间隔值。而在虚线上的点便叫做支持向量Supprot Verctor。

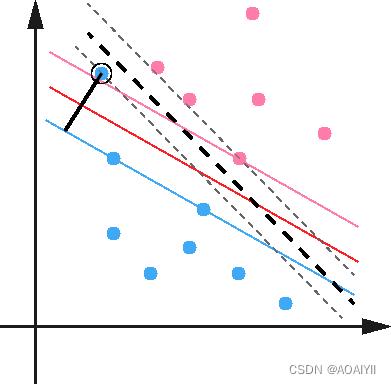
3.实际上，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去(如下图)；

4.线性不可分映射到高维空间，可能会导致维度大小高到可怕(19维乃至无穷维的例子)，导致计算复杂。核函数的价值在于它虽然也是讲特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算。

5.使用松弛变量处理数据噪音

sklearn中SVM的结构，及各个参数说明如下

sklearn.svm.SVC ：

C：C-SVC的惩罚参数C?默认值是1.0
C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。
kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
　　0 – 线性：u’v
　　 1 – 多项式：(gamma*u’v + coef0)^degree
　　2 – RBF函数：exp(-gamma|u-v|^2)
　　3 –sigmoid：tanh(gammau’v + coef0)
degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。
gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features
coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
probability ：是否采用概率估计？.默认为False
shrinking ：是否采用shrinking heuristic方法，默认为true
tol ：停止训练的误差值大小，默认为1e-3
cache_size ：核函数cache缓存大小，默认为200
class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weightC(C-SVC中的C)
verbose ：允许冗余输出？
max_iter ：最大迭代次数。-1为无限制。
decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3
random_state ：数据洗牌时的种子值，int值

主要调节的参数有：C、kernel、degree、gamma、coef0。

三、实验环境

Python 3.9

Jupyter

四、实验内容

利用sklearn中的svm支持向量机对fetch_lfw_people数据进行人脸识别，并将预测结果可视化。

五、实验步骤

1.准备数据

1.首先需要的数据有：joblib、lfw_funneled、pairs.txt、pairsDevTest.txt、pairsDevTrain.txt
注意：也可以直接使用fetch_lfw_people这个函数是用来加载lfw人脸识别数据集的函数。


2.其次在其路径中创建一个文件

3.最后在文件里创建一个ipynb文件

SVM(Support Vector Machine)指的是支持向量机，是常见的一种判别方法。在机器学习领域，是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。

2.业务理解

利用sklearn中的svm支持向量机做人脸识别

该数据集是在互联网上收集的著名人物的JPEG图片的集合，所有详细信息可在官方网站上获得：

http://scikit-learn.org/stable/datasets/labeled_faces.html

http://vis-www.cs.umass.edu/lfw/

每张照片都以一张脸为中心。每个通道的每个像素（RGB中的颜色）由范围为0.0-1.0的浮点编码。

该任务称为面部识别（或识别）：给定面部图片，找到给定训练集（图库）的人的姓名。

3.数据理解

1.在刚才新建的ipynb文件中，编写代码，导入数据

import numpy as np  
import matplotlib.pyplot as plt  
import seaborn as sns;sns.set()  
from matplotlib.font_manager import  FontProperties  
#导入fetch_lfw_people  
from sklearn.datasets import  fetch_lfw_people  
#fetch_lfw_people函数加载人脸识别数据集  
faces = fetch_lfw_people(min_faces_per_person=60)  
#输出人名
print(faces.target_names)  
#输出人脸数据结构
print(faces.images.shape)

说明：
fetch_lfw_people这个函数是用来加载lfw人脸识别数据集的函数，返回data,images,target,target_names.分别是向量化的人脸数据，人脸，人脸对应的人名编号，人名

关于此函数参数的描述：min_faces_per_person：提取的数据集将只保留至少具有min_faces_per_person个不同人的图片

具体数据可参考官方文档：http://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_lfw_people.html

2.绘制图形

#使用subplots 画图  
fig,ax = plt.subplots(3,5)  
#在每一行上绘制子图  
for i,axi in enumerate(ax.flat):  
    axi.imshow(faces.images[i],cmap="bone")  
    axi.set(xticks=[],yticks=[],xlabel=faces.target_names[faces.target[i]])  
plt.show()

注释： 使用subplots会返回两个东西，一个是matplotlib.figure.Figure，也就是fig，另一个是Axes object or array of Axes objects，也就是代码中的ax；把f理解为你的大图，把ax理解为包含很多小图对象的array；所以下面的代码就使用ax[0][0]这种从ax中取出实际要画图的小图对象；画出的图如下所示；

4.数据划分为测试集和训练集

1.划分训练集和测试集

from sklearn.model_selection import  train_test_split  
Xtrain,Xtest,ytrain,ytest=train_test_split(faces.data,faces.target,random_state=42)  
Xtrain

5.模型构建

1.建立模型，计算人脸数据集上的PCA（特征脸）（处理为标记的）

from sklearn.svm import  SVC  
from sklearn.decomposition import  PCA  
from sklearn.pipeline import make_pipeline  
 
pca = PCA(n_components=150,whiten=True,random_state=42,svd_solver='randomized')  
svc = SVC(kernel='rbf',class_weight='balanced')  
model = make_pipeline(pca,svc)

说明：PCA主要是通过奇异值分解将数据映射到低纬度的空间（正交去相关）。PCA在数据降维，数据压缩，特征提取有很大贡献。在此，我们利用PCA提取150个主要特征，并将人脸数据全部映射到150维度，通过这150维人脸特征作为训练数据训练基于rbf kernel的SVM，模型差不多有0.85的准确率

6.参数调整

1.param_grid把参数设置成了不同的值，C：权重；gamma：多少的特征点将被使用，因为我们不知道多少特征点最好，选择了不同的组合

#参数调整  
from sklearn.model_selection import GridSearchCV  
param_grid = "svc__C":[1,5,10,50],"svc__gamma":[0.0001,0.0005,0.001,0.005]  
#把所有我们所列参数的组合都放在SVC里面进行计算，最后看出哪一组函数的表现度最好  
grid = GridSearchCV(model,param_grid)  
%time grid.fit(Xtrain,ytrain)  
print(grid.best_params_)

说明：svc__C为10svc__gamma为0.001表现度最好

7.预测测试集的人名编号

model = grid.best_estimator_  
model


预测测试集：

yfit = model.predict(Xtest)  
yfit

说明：结果为预测的人名编号

8.显示预测结果

1.数据可视化，把需要打印的图打印出来,预测的结果和实际结果一致，人名字体颜色为黑色，否则为红色

#显示预测结果  
fig,ax = plt.subplots(4,6)  
for  i,axi in enumerate(ax.flat):  
    axi.imshow(Xtest[i].reshape(62,47),cmap="bone")  
    axi.set(xticks=[],yticks=[])  
    #设置y轴上的标签  
    axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],color="black" if yfit[i]==ytest[i] else "red")  
fig.suptitle("Incorrect Labels in Red",size=14)  
plt.show()

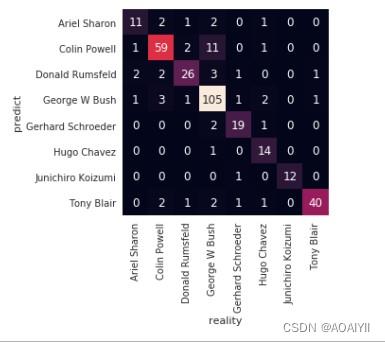
9.分析预测结果的准确性

使用seaborn.heatmap绘制颜色编码矩阵

解释：seaborn.heatmap()将矩形数据绘制为颜色编码矩阵。

seaborn.heatmap（data，vmin = None，vmax = None，cmap = None，center = None，robust = False，annot = None，fmt =‘。2g’，annot_kws = None，linewidths = 0，linecolor =‘white’，cbar =是的，cbar_kws =无，cbar_ax =无，square = False，xticklabels =‘auto’，yticklabels =‘auto’，mask = None，ax = None，** kwargs ）

重要参数说明：

  • data：矩形数据集

  • square：布尔值，可选，如果为True，则将Axes方面设置为“相等”，以使每个单元格为方形

  • annot：bool或矩形数据集，可选，如果为True，则在每个单元格中写入数据值。如果数组具有相同的形状data，则使用此选项来注释热图而不是原始数据。

  • fmt：string，可选，添加注释时要使用的字符串格式代码。

  • cbar：布尔值，可选，是否绘制颜色条

  • xticklabels，yticklabels：“auto”，bool，list-like或int，optional。如果为True，则绘制数据框的列名称。如果为False，则不绘制列名称。如果是列表，则将这些替代标签绘制为xticklabels。如果是整数，则使用列名称，但仅绘制每个n标签。如果是“自动”，请尝试密集绘制不重叠的标签

#分析预测结果的准确性  
from sklearn.metrics import  confusion_matrix  
#混淆矩阵  
mat = confusion_matrix(ytest,yfit)  
#绘制热图  
sns.heatmap(mat.T,square=True,annot=True,fmt="d",cbar=False,xticklabels=faces.target_names,yticklabels=faces.target_names)  
plt.rcParams["font.family"]="SimHei"  
plt.xlabel("真实值")  
plt.ylabel("预测值")  
plt.show()

10.完整代码

import numpy as np  
import matplotlib.pyplot as plt  
import seaborn as sns;sns.set()  
from matplotlib.font_manager import  FontProperties  
#导入fetch_lfw_people  
from sklearn.datasets import  fetch_lfw_people  
#fetch_lfw_people函数加载人脸识别数据集  
faces = fetch_lfw_people(min_faces_per_person=60)  
#输出人名
print(faces.target_names)  
#输出人脸数据结构
print(faces.images.shape)


#使用subplots 画图  
fig,ax = plt.subplots(3,5)  
#在每一行上绘制子图  
for i,axi in enumerate(ax.flat):  
    axi.imshow(faces.images[i],cmap="bone")  
    axi.set(xticks=[],yticks=[],xlabel=faces.target_names[faces.target[i]])  
plt.show()


#划分训练集和测试集  
from sklearn.model_selection import  train_test_split  
Xtrain,Xtest,ytrain,ytest=train_test_split(faces.data,faces.target,random_state=42)  
Xtrain  


 #建模  
from sklearn.svm import  SVC  
from sklearn.decomposition import  PCA  
from sklearn.pipeline import make_pipeline  
#计算人脸数据集上的PCA(特征脸)(处理为未标记的)  
pca = PCA(n_components=150,whiten=True,random_state=42,svd_solver='randomized')  
svc = SVC(kernel='rbf',class_weight='balanced')  
model = make_pipeline(pca,svc)   


#参数调整  
from sklearn.model_selection import GridSearchCV  
param_grid = "svc__C":[1,5,10,50],"svc__gamma":[0.0001,0.0005,0.001,0.005]  
#把所有我们所列参数的组合都放在SVC里面进行计算，最后看出哪一组函数的表现度最好  
grid = GridSearchCV(model,param_grid)  
%time grid.fit(Xtrain,ytrain)  
print(grid.best_params_)  


model = grid.best_estimator_  
model  
yfit = model.predict(Xtest)  
yfit  


#显示预测结果  
fig,ax = plt.subplots(4,6)  
for  i,axi in enumerate(ax.flat):  
    axi.imshow(Xtest[i].reshape(62,47),cmap="bone")  
    axi.set(xticks=[],yticks=[])  
    #设置y轴上的标签  
    axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],color="black" if yfit[i]==ytest[i] else "red")  
fig.suptitle("Incorrect Labels in Red",size=14)  
plt.show() 



#分析预测结果的准确性  
from sklearn.metrics import  confusion_matrix  
#混淆矩阵  
mat = confusion_matrix(ytest,yfit)  
#绘制热图  
sns.heatmap(mat.T,square=True,annot=True,fmt="d",cbar=False,xticklabels=faces.target_names,yticklabels=faces.target_names)  
plt.rcParams["font.family"]="SimHei"  
plt.xlabel("真实值")  
plt.ylabel("预测值")  
plt.show()

总结

逻辑回归可以分为线性与非线性，也可以根据类的个数分为二分类与多分类问题，使用时需要灵活应用，能够构造损失函数并求梯度，同时能够用算法实现并进行训练预测。

事实上，细心的同学会发现，在逻辑回归中，我们发现是多个输入（即p个指标），最终输出一个结果（0或1），处理过程是输入乘上权重w加偏置b，再对结果用sigmoid 函数处理，这个过程其实很接近于神经网络了，而逻辑回归的模型更接近于感知机。对于神经网络，它不只有输入和输出两层，而且增加了更多的隐藏层，每一层的处理结果都作为下一层的输入，那么它的损失函数与梯度的求解也将更加复杂，模型也复杂许多。

以上是关于基于支持向量机SVM的脑部肿瘤识别，脑电波样本熵提取的主要内容，如果未能解决你的问题，请参考以下文章

基于支持向量机(SVM)进行人脸识别

图像识别基于svm支持向量机算法表情识别matlab源码

手写数字识别基于支持向量机SVM实现手写数字识别matlab源码含GUI

手写数字识别基于支持向量机SVM实现手写数字识别matlab源码含GUI

基于并联SVM支持向量机训练HOG特征提取的人员目标提取

机器学习：基于支持向量机（SVM）进行人脸识别预测