Python实现Imagenet数据集的合并和拆分

Posted 2023-04-09 安静到无声

Python实现Imagenet数据集的合并和拆分

1. 合并Imagenet

任务需求

文件夹形式为一个数据集MyImagenet，路径为/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val，val文件夹又有若干的类别子文件夹，子文件夹是每一个类别的图片，我们要将所有的文件都移动到/home/lihuanyu/code/03AdaBins/MyImagenet_disorganize/val这一个文件夹下面，不设定各种子文件夹。

要求点

1. 输入文件夹路径为/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val，输出文件夹的路径为/home/lihuanyu/code/03AdaBins/MyImagenet_disorganize/val，如果没有该文件夹则进行创建。
2. 将/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val下所有子文件夹下图片，都复制到/home/lihuanyu/code/03AdaBins/MyImagenet_disorganize/val这个文件夹中。
3. 要有用python语言
4. 需要打印处理流程：处理到那一张图片（要计数）和处理完成的标志。

代码实现

这段代码的作用是将指定文件夹下的所有文件（包括子文件夹中的文件）复制到另外一个目录中。

首先，定义了两个变量src_path和dst_path，分别代表源文件夹路径和目标文件夹路径。然后，判断目标文件夹是否存在，若不存在则使用os.mkdir()函数创建该目录。

接下来使用os.walk()函数遍历源目录下的所有子目录和文件，得到每个文件的完整路径。对于每个文件，执行shutil.copy()函数将其复制到目标文件夹中，并打印处理进度信息。计数器count会随着处理文件的数量逐渐累加。

最后，当源目录下所有文件都处理完成后，输出处理完成的标志信息。

需要注意的是，目标文件夹中有相同命名的文件时，shutil.copy()函数会自动覆盖原文件。如果在复制过程中需要保留原文件，请使用shutil.copy2()函数。

import os  
import shutil  
  
# 输入文件夹路径和输出文件夹路径  
src_path = '/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val'  
dst_path = '/home/lihuanyu/code/03AdaBins/MyImagenet_disorganize/val'  
  
# 如果目标文件夹不存在，则创建  
if not os.path.exists(dst_path):  
    os.mkdir(dst_path)  
  
# 计数器初始化  
count = 0  
  
# 遍历源目录下的所有子目录和文件  
for root, dirs, files in os.walk(src_path):  
    # 处理当前目录下的所有文件  
    for file in files:  
        # 构造源文件和目标文件的完整路径  
        src_file = os.path.join(root, file)  
        dst_file = os.path.join(dst_path, file)  
        # 复制文件到目标目录  
        shutil.copy(src_file, dst_file)  
        # 计数器加1  
        count += 1  
        # 打印处理进度  
        print('正在处理第张图片: '.format(count, src_file))  
  
# 处理完成的标志  
print('所有图片已处理完成！')

2. 拆分Imagenet

在数据集合并加工完毕后，我们将处理好的图像保存在一个文件夹中，例如/home/lihuanyu/code/03AdaBins/MyImagenet_disorganize/val。不过，在后续的模型预训练中，我们需要重新组织数据集，将所有图片按照标签分类，并分别存储在以标签命名的文件夹中。

构建类别名称和类别编号关系字典

要求点1

1. 以/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val文件夹为例，它的每个文件夹名字都代表了类别名称，而文件夹下的文件是图片，我们从每个类别文件夹随机抽取一个图片，假设抽到n02009912_197.JPEG为例，其中字符串下划线_之前的字符串n02009912是代表类别的编号。
2. 基于此可以构建图片类别名称与类别编号对应的关系字典。
3. Python代码实现。
4. 要求打印出来。

代码实现

import os  
import random  
  
# 定义数据集路径和每个子目录下需要随机选择的图片数量  
data_path = '/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val'  
num_images_per_class = 1  
  
# 构建图片类别名称与类别编号对应的关系字典  
image_dict =   
for label_name in os.listdir(data_path):  
    # 获取该类别的编号  
    label_idx = os.listdir(os.path.join(data_path, label_name))[0].split('_')[0]  
    image_dict[label_name] = label_idx  
  
print(image_dict)

这段代码用于构建图片类别名称与类别编号对应的关系字典，具体解释如下：

• data_path：定义数据集路径。
• num_images_per_class：定义每个子目录下需要随机选择的图片数量，此处设置为1。
• image_dict：定义一个字典，用于存储图片类别名称与类别编号之间的对应关系。
• for label_name in os.listdir(data_path):：遍历数据集目录下的所有子目录（即类别名称）。
• os.listdir(os.path.join(data_path, label_name))：获取当前类别文件夹下的所有文件（即图片），并返回一个列表。
• [0]：获取该列表中的第一个元素，即选取一个随机的图片。
• .split('_')[0]：将该图片的文件名按照下划线分隔成两部分，然后取第一部分作为该图片的类别编号。
• image_dict[label_name] = label_idx：将该图片的类别名称作为字典的键，将该图片的类别编号作为字典的值。

该段代码的主要作用是在不知道每个类别文件夹下有多少张图片的情况下，随机选取每个类别文件夹下的一张图片，并将其所属的类别编号与类别名称存储到字典中，方便后续的分类模型训练和评估。

结果呈现

'rule': 'n04118776', 'gartersnake': 'n01735189', 'mobilehome': 'n03776460', 'schoolbus': 'n04146614', 'pooltable': 'n03982430', 'washer': 'n04554684', 'wool': 'n04599235', 'ModelT': 'n03777568', 'beerbottle': 'n02823428', 'whitefox': 'n02120079', 'birdhouse': 'n02843684', 'Bread': 'n07684084', 'warplane': 'n04552348', 'web': 'n06359193', 'trimaran': 'n04483307', 'chickadee': 'n01592084', 'cucumber': 'n07718472', 'Siamese': 'n02123597', 'carton': 'n02971356', 'missile': 'n03773504', 'wolfspider': 'n01775062', 'husky': 'n02109961', 'catamaran': 'n02981792', 'Oriole': 'n01531178', 'recreationalvehicle': 'n04065272', 'digitalclock': 'n03196217', 'watertower': 'n04562935', 'butternutsquash': 'n07717556', 'ostrich': 'n01518878', 'radiotelescope': 'n04044716', 'Grasshopper': 'n02226429', 'reflexcamera': 'n04069434', 'moped': 'n03785016', 'coffeepot': 'n03063689', 'firetruck': 'n03345487', 'matchstick': 'n03729826', 'revolver': 'n04086273', 'artichoke': 'n07718747', 'tileroof': 'n04435653', 'Tram': 'n04335435', 'chimpanzee': 'n02481823', 'gorilla': 'n02480855', 'hourglass': 'n03544143', 'thatch': 'n04417672', 'Persiancat': 'n02123394', 'hyaena': 'n02117135', 'tank': 'n04389033', 'badger': 'n02447366', 'rocker': 'n04099969', 'horn': 'n03394916', 'trifle': 'n07613480', 'convertible': 'n03100240', 'piano': 'n04515003', 'butterfly': 'n02281787', 'bottlecap': 'n02877765', 'keypad': 'n03085013', 'stonewall': 'n04326547', 'leatherbackturtle': 'n01665541', 'streetsign': 'n06794110', 'goldfish': 'n01443537', 'soapdispenser': 'n04254120', 'cassetteplayer': 'n02979186', 'golfball': 'n03445777', 'Recordsheet': 'n03841143', 'measuringcup': 'n03733805', 'malamute': 'n02110063', 'Americanegret': 'n02009912', 'dustcart': 'n03417042', 'lizard': 'n01675722', 'desktopcomputer': 'n03180011', 'projector': 'n04009552', 'gibbon': 'n02483362', 'Rottweiler': 'n02106550', 'stoplight': 'n06874185', 'SaintBernard': 'n02109525', 'vase': 'n04522168', 'monitor': 'n03782006', 'tabby': 'n02123045', 'tablelamp': 'n04380533', 'carrier': 'n02687172', 'dishrag': 'n03207743', 'runningshoe': 'n04120489', 'crocodile': 'n01697457', 'person': 'n03450230', 'suspensionbridge': 'n04366367', 'limpkin': 'n02013706', 'numbfish': 'n01496331', 'fly': 'n02190166', 'carwheel': 'n02974003', 'freightcar': 'n03393912', 'submarine': 'n04347754', 'mask': 'n03724870', 'minibus': 'n03769881', 'jeep': 'n03594945', 'daybed': 'n04344873', 'chiffonier': 'n03016953', 'greatgreyowl': 'n01622779', 'taxi': 'n02930766', 'yurt': 'n04613696', 'leopard': 'n02128385'

基于要求点1实现合并数据集的拆分

要求点2

1. 通过要点1获得的图片类别名称与类别编号对应的关系字典image_dict，读取字典的键，在该路径下/home/lihuanyu/code/03AdaBins/MyImagenet_merge/val，以键名创建对应文件夹。
2. 遍历/home/lihuanyu/code/03AdaBins/img_data/MyImagenet/val的图片文件名，假设文件名为n02009912_197.JPEG，截取_前面的字符串，并判断字符串属于那个那个键对应的键值，匹配成功后，将图片复制到对应的文件夹。

代码实现

这段代码实现了将一个数据集中的各个子文件夹下的一定数量的图片（num_images_per_class）随机选择后合并到同一个文件夹下的相应子文件夹里。具体来说，代码首先指定了数据集所在的路径 data_path 和每个子目录下需要随机选择的图片数量 num_images_per_class，接着用 get_key_by_value 函数通过图像 ID 在 image_dict 字典中查找对应的类别名称，然后根据该名称创建相应的文件夹，建立好文件夹和文件之间的映射关系后，用 shutil 库的 copy 函数将指定的图片从原数据集路径 data_path 复制到新路径（即将所有子文件夹的图片复制到同一文件夹下相应子文件夹里）。整个过程会输出完成复制的图片数量。

import os  
import shutil  
  
# 定义图片数据集路径和每个子目录下需要随机选择的图片数量  
type = 'val'  
  
data_path = '/home/lihuanyu/code/03AdaBins/MyImagenet_disorganize/'.format(type)  #未合并的文件夹位置  
num_images_per_class = 1  
  
def get_key_by_value(dict_obj, value):  
    """  
    返回一个字典中某个值对应的键  
    :param dict_obj: 字典对象  
    :param value: 字典中的值  
    :return: 与给定值对应的键，若未找到则返回 None    """    for k, v in dict_obj.items():  
        if v == value:  
            return k  
    return None  
i = 0  
# 根据字典的键名创建对应的文件夹  
for label_name in image_dict.keys():  
    if not os.path.exists(os.path.join('/home/lihuanyu/code/03AdaBins/MyImagenet_merge/'.format(type), label_name)): #合并的文件夹位置  
        os.makedirs(os.path.join('/home/lihuanyu/code/03AdaBins/MyImagenet_merge/'.format(type), label_name))  #合并的文件夹位置  
    for filename in os.listdir(os.path.join('/home/lihuanyu/code/03AdaBins/MyImagenet_process/'.format(type),label_name)):  
        label_idx = filename.split('_')[0]  
  
        key_idx = get_key_by_value(image_dict,label_idx)  
        src_path = os.path.join(data_path, filename)  
        dst_path = os.path.join('/home/lihuanyu/code/03AdaBins/MyImagenet_merge/'.format(type), key_idx, filename)  
        shutil.copy(src_path, dst_path)  
        i = i + 1  
        print("完成第个图片".format(i,filename))

结果呈现

数据结构--并查集的原理及实现

一，并查集的介绍

 并查集（Union/Find）从名字可以看出，主要涉及两种基本操作:合并和查找。这说明，初始时并查集中的元素是不相交的，经过一系列的基本操作(Union)，最终合并成一个大的集合。

而在某次合并之后，有一种合理的需求：某两个元素是否已经处在同一个集合中了？因此就需要Find操作。

并查集是一种 不相交集合 的数据结构，设有一个动态集合S={s1，s2，s3，.....sn}，每个集合通过一个代表来标识，代表 就是动态集合S 中的某个元素。

比如，若某个元素 x 是否在集合 s1 中(Find操作)，返回集合 s1 的代表元素即可。这样，判断两个元素是否在同一个集合中也是很方便的，只要看find(x) 和 find(y) 是否返回同一个代表即可。

为什么是动态集合S呢？因为随着Union操作，动态集合S中的子集合个数越来越少。

数据结构的基本操作决定了它的应用范围，对并查集而言，一个简单的应用就是判断无向图的连通分量个数，或者判断无向图中任何两个顶点是否连通。

 

二，并查集的存储结构及实现分析

①存储结构

并查集(大S)由若干子集合si构成，并查集的逻辑结构就是一个森林。si表示森林中的一棵子树。一般以子树的根作为该子树的代表。

而对于并查集的存储结构，可用一维数组和链表来实现。这里主要介绍一维数组的实现。

根据前面介绍的基本操作再加上存储结构，并查集类的实现架构如下：

public class DisjSets {
    private int[] s;
    private int count;//记录并查集中子集合的个数(子树的个数)

       public DisjSets(int numElements) {
       //构造函数，负责初始化并查集
       }

        public void unionByHeight(int root1, int root2){    
        //union操作
       }

       public int find(int x){
       //find 操作
      }
}

 

由于Find操作需要找到该子集合的代表元素，而代表元素是树根，因此需要保存树中结点的父亲，对于每一个结点，如果知道了父亲，沿着父结点链就可以最终找到树根。

为了简单起见，假设一维数组s中的每个元素 s[i] 表示该元素 i 的父亲。这里有两个需要注意的地方：①我们用一维数组来存储并查集，数组的元素s[i]表示的是结点的父亲的位置。②数组元素的下标 i 则是结点的标识。如：s[5]=4，表示：结点5 的父亲 是结点4。

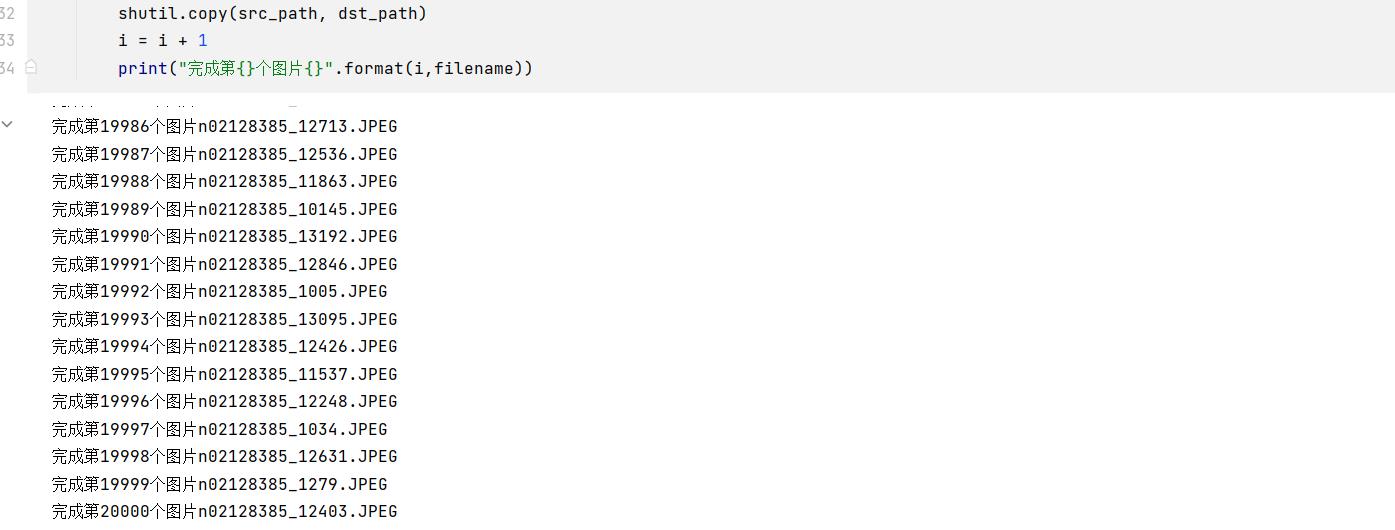
假设有并查集中6个元素，初始时，所有的元素都相互独立，处在不同的集合中：

对应的一维数组初始化如下：

因为，初始时每个元素代表一个集合，该元素本身就是树根。树根的父结点用 -1 来表示。代码实现如下：

1     public DisjSets(int numElements) {
2         s = new int[numElements];
3         count = numElements;
4         //初始化并查集,相当于新建了s.length 个互不相交的集合
5         for(int i = 0; i < s.length; i++)
6             s[i] = -1;//s[i]存储的是高度(秩)信息
7     }

 

②基本操作实现

Union操作就是将两个不相交的子集合合并成一个大集合。简单的Union操作是非常容易实现的，因为只需要把一棵子树的根结点指向另一棵子树即可完成合并。

比如合并 节点3 和节点4：

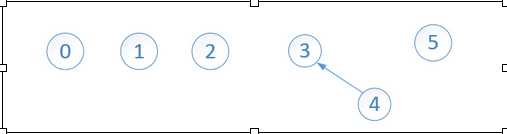
这里的合并很随意，把任意一棵子树的结点指向另一棵子树结点就完成了合并。

1     public void union(int root1, int root2){
2         s[root2] = root1;//将root1作为root2的新树根
3     }

但是，这只是一个简单的情况，如果待合并的两棵子树很大，而且高度不一样时，如何使得合并操作生成的新的子树的高度最小？因为高度越小的子树Find操作越快。

后面会介绍一种更好的合并策略，以支持Quick Union/Find。

 

Find操作就是查找某个元素所在的集合，返回该集合的代表元素。在union(3,4) 和 union(1,2)后，并查集如下：

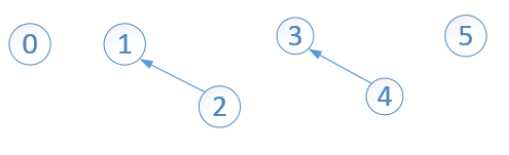
此时的一维数组如下：

此时一共有4个子集合。第一个集合的代表元素为0，第二个集合的代表元素为1，第三个集合的代表元素为3，第四个集合的代表元素为5，故：

find(2)返回1，find(0)返回0。因为 结点3 和 结点4 在同一个集合内，find(4)返回3，find(3)返回3。

1     public int find(int x){
2         if(s[x] < 0)
3             return x;
4         else
5             return find(s[x]);
6     }

这里find(int x)返回的是最里层递归执行后，得到的值。由于只有树根的父结点位置小于0，故返回的是树根结点的标识。

（数组中索引 i 处的元素 s[i] 小于0，表示 结点i 是根结点.....）

 

Union/Find的改进----Quick Union/Find

 上面介绍的Union操作很随意：任选一棵子树，将另一棵子树的根指向它即完成了合并。如果一直按照上述方式合并，很可能产生一棵非常不平衡的子树。

比如在上面的基础上union(2,3)后

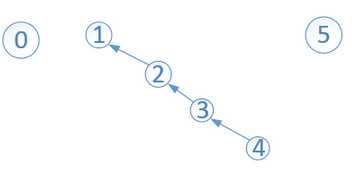
树越来越高了，此时会影响到Find操作的效率。比如，find(4)时，会一直沿着父结点遍历直到根，4-->3-->2-->1

这里引入一种新的合并策略，这是一种启发式策略，称之为按秩合并：将秩小的子树的根指向秩大的子树的根。

秩的定义：对每个结点，用秩表示结点高度的一个上界。为什么是上界？

因为路径压缩不完全与按高度求并兼容。路径压缩会改变树的高度，这样在Union操作之前，我们就无法获得子树的高度的精确值，因此就不计算高度的精确值，而是存储每棵树的高度的估计值，这个值称之为秩。（关于路径压缩在后面的Find操作中会详细介绍）

说了这么多，按秩求并就是在合并之前，先判断下哪棵子树更高，让矮的子树的根指向高的子树的根。

 除了按高度求并之外，还可以按大小求并，即先判断下哪棵子树含有的结点数目多，让较小的子树的根指向较大的子树的根。

 对于按高度求并，需要解释下数组中存储的元素：是高度的负值再减去1。这样，初始时，所有元素都是-1，而树根节点的高度为0，s[i]=-1。

按高度求并的代码如下：

 1 /**
 2      * 
 3      * @param root1 并查集中以root1为代表的某个子集
 4      * @param roo2 并查集中以root2为代表的某个子集
 5      * 按高度(秩)合并以root1 和 root2为代表的两个集合
 6      */
 7     public void unionByHeight(int root1, int root2){
 8         if(find(root1) == find(root2))
 9             return;//root1 与 root2已经连通了
10         
11         if(s[root2] < s[root1])//root2 is deeper
12             s[root1] = root2;
13         else{
14             if(s[root1] == s[root2])//root1 and root2 is the same deeper
15                 s[root1]--;//将root1的高度加1
16             s[root2] = root1;//将root2的根(指向)更新为root1
17         }
18         
19         count--;//每union一次,子树数目减1
20     }

 

使用了路径压缩的Find的操作

上面程序代码find方法只是简单地把待查找的元素所在的根返回。路径压缩是指，在find操作进行时，使find查找路径中的顶点(的父亲)都直接指向为树根（这很明显地改变了子树的高度）

如何使find查找路径中经过的每个顶点都直接指向树根呢？只需要小小改动一下就可以了，这里用到了非常神奇的递归。修改后的find代码如下：

1     public int find(int x){
2         if(s[x] < 0)//s[x]为负数时,说明 x 为该子集合的代表(也即树根), 且s[x]的值表示树的高度
3             return x;
4         else 
5             return s[x] = find(s[x]);//使用了路径压缩,让查找路径上的所有顶点都指向了树根(代表节点)
6             //return find(s[x]); 没有使用 路径压缩
7     }

因为递归最终得到的返回值是根元素。第5行将根元素直接赋值给s[x]，s[x]在每次递归过程中相当于结点x的父结点指针。

 

关于路径压缩对按”秩“求并的兼容性问题

上面的unionByHeight(int , int)是按照两棵树的高度来进行合并的。但是find操作中的路径压缩会对树的高度产生影响。使用了路径压缩后，树的高度变化了，但是数组并没有更新这个变化。因为无法更新！！（我们没有在Find操作中去计算原来的树的高度，然后再计算新的树的高度，这样不现实，复杂度太大了）

举个例子：

依次高度unionByHeight(3, 4)、unionByHeight(1, 3)、unionByHeight(1, 0)后，并查集如下：

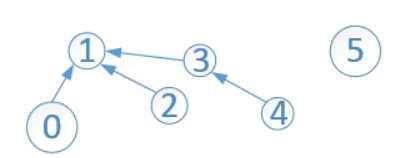
此时，数组中的元素如下：

可以看出，此时只有两棵子树，一棵根结点为1，另一棵只有一个结点5。结点1的s[1]=-3，它所表示是该子树的高度为2，如果此时执行find(4)，会改变这棵树的高度！但是，数组s中存储的根的高度却没有更新，只会更新查找路径上的顶点的高度。执行完find(4)后，变成：

查找路径为 4-->3-->1，find(4)使得查找路径上的所有顶点的父结点指向了根。如，将结点4 指向了根。但是没有根结点的高度（没有影响树根的秩），因为s[1]的值仍为-3

-3表示的高度为2，但是树的高度实际上已经变成了1

执行find(4)之后，树实际上是这样的：

 

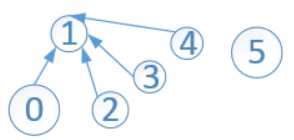
（关于路径压缩对按秩合并有影响，我一直有个疑问，希望有大神指点啊）。。。。

路径压缩改变了子树的高度，而这个高度是按秩求的依据。，而且当高度改变之后，我们是无法更新这个变化了的高度的。那这会不会影响按秩求并的正确性？或者说使按秩求并达不到减小新生成的子树的高度的效果？

 

四，并查集的应用

 并查集数据结构非常简单，基本操作也很简单。但是用途感觉很大。比如，求解无向图中连通分量的个数，生成迷宫……

 这些应用本质上就是：初始时都是一个个不连通的对象，经过一步步处理，变成连通的了。。。。。

如迷宫，初始时，起点和终点不连通，随机地打开起点到终点路径上的一个方向，直至起点和终点连通了，就生成了一个迷宫。

如，无向图的连通分量个数，初始时，将无向图中各个顶点视为不连通的子集合，对图中每一条边，相当于union这条边对应的两个顶点分别所在的集合，直至所有的边都处理完后，还剩下的集合的个数即为连通分量的个数。

 

五，完整代码如下：

  1 package mark_allen_weiss.c8;
  2 
  3 public class DisjSets {
  4     private int[] s;
  5     private int count;//记录并查集中子集合的个数(子树的个数)
  6     
  7     
  8     public DisjSets(int numElements) {
  9         s = new int[numElements];
 10         count = numElements;
 11         //初始化并查集,相当于新建了s.length 个互不相交的集合
 12         for(int i = 0; i < s.length; i++)
 13             s[i] = -1;//s[i]存储的是高度(秩)信息
 14     }
 15     
 16     /**
 17      * 
 18      * @param root1 并查集中以root1为代表的某个子集
 19      * @param roo2 并查集中以root2为代表的某个子集
 20      * 按高度(秩)合并以root1 和 root2为代表的两个集合
 21      */
 22     public void unionByHeight(int root1, int root2){
 23         if(find(root1) == find(root2))
 24             return;//root1 与 root2已经连通了
 25         
 26         if(s[root2] < s[root1])//root2 is deeper
 27             s[root1] = root2;
 28         else{
 29             if(s[root1] == s[root2])//root1 and root2 is the same deeper
 30                 s[root1]--;//将root1的高度加1
 31             s[root2] = root1;//将root2的根(指向)更新为root1
 32         }
 33         
 34         count--;//每union一次,子树数目减1
 35     }
 36     
 37     public void union(int root1, int root2){
 38         s[root2] = root1;//将root1作为root2的新树根
 39     }
 40     
 41     
 42     public void unionBySize(int root1, int root2){
 43         
 44         if(find(root1) == find(root2))
 45             return;//root1 与 root2已经连通了
 46         
 47         if(s[root2] < s[root1])//root2 is deeper
 48             s[root1] = root2;
 49         else{
 50             if(s[root1] == s[root2])//root1 and root2 is the same deeper
 51                 s[root1]--;//将root1的高度加1
 52             s[root2] = root1;//将root2的根(指向)更新为root1
 53         }
 54         
 55         count--;//每union一次,子树数目减1
 56     }
 57     
 58     
 59     public int find(int x){
 60         if(s[x] < 0)//s[x]为负数时,说明 x 为该子集合的代表(也即树根), 且s[x]的值表示树的高度
 61             return x;
 62         else 
 63             return s[x] = find(s[x]);//使用了路径压缩,让查找路径上的所有顶点都指向了树根(代表节点)
 64             //return find(s[x]); 没有使用 路径压缩
 65     }
 66     
 67     public int find0(int x){
 68         if(s[x] < 0)
 69             return x;
 70         else 
 71             return find0(s[x]);
 72     }
 73     
 74     
 75     public int size(){
 76         return count;
 77     }
 78     
 79     //for test purpose
 80     public static void main(String[] args) {
 81         DisjSets dSet = new DisjSets(6);
 82         dSet.unionBySize(1, 2);
 83         
 84         for(int i : dSet.s)
 85             System.out.print(i + " ");
 86         
 87         dSet.unionBySize(3, 4);
 88         
 89         System.out.println();
 90         for(int i : dSet.s)
 91             System.out.print(i + " ");
 92         
 93         System.out.println();
 94         dSet.unionBySize(1, 3);
 95         for(int i : dSet.s)
 96             System.out.print(i + " ");
 97         
 98         System.out.println();
 99         dSet.unionBySize(1, 0);
100         for(int i : dSet.s)
101             System.out.print(i + " ");
102         
103         System.out.println();
104         int x = dSet.find(4);
105         System.out.println(x);
106         
107         for(int i : dSet.s)
108             System.out.print(i + " ");
109         
110         System.out.println("
size:" + dSet.size());
111     }
112 }

 

六，参考资料

http://blog.csdn.net/dm_vincent/article/details/7655764

《算法导论》第二版

《数据结构与算法分析》JAVA语言描述--Mark Allen Weiss