用梯度下降的方式来拟合曲线

Posted 2023-04-09 1037号森林里一段干木头

文章目录

• • 1. 简述
  • 2. 理论原理
  • • 以二次函数为例
    • 整体的梯度下降步骤：
  • 3. 编码实现
  • • 初始化权重矩阵
    • 计算损失和梯度
    • 更新权重
  • 4. 结果
  • • 首先对上一篇文章中的真实数据拟合。
    • 测试拟合高次曲线方程
    • • 数据是2阶的，拟合方程是2阶的
      • 数据是4阶的，拟合方程也是4阶的。
      • 方程是4阶的，拟合方程是3阶的，（测试欠拟合）
      • 方程式4阶的，拟合方程是5阶的，（测试过拟合）
      • 数据是2阶的，方程是4阶的 (测试过拟合)
  • 5. 总结
  • 6. 还有可做的可视化方向
  • 完整源码

1. 简述

在之前的一篇文章opencv C++ 曲线拟合中为了拟合一条二次曲线，用超定方程的理论转为求最小二乘的方式来做，这是一个解析的方式求的解，也是全局最优的解。在深度学习中学到的函数是非常复杂的，不能保证是凸的，也没办法从解析的角度来计算一个最优解，这时最有效常用的方法就是梯度下降，为了加深对梯度下降的理解，所以这里以梯度下降来拟合多项式函数来探索一下。

2. 理论原理

以二次函数为例

设函数为$f(x)=a_0+a_{1}x+a_2{x}^2$,确定一组$a_0,a_1,a_2$的值，也就确定了二次函数，所以可以认为一组$a_0,a_1,a_2$值就是一个模型了。

样本为$(x,y)$， $\hat{y}$为模型的预测值，要评价一个模型好不好，我们可以用残差总和(loss)来表示，残差总和越小，模型越好。那我们的目标就是找一组$a_0,a_1,a_2$的值，使得下面的式子：
$$loss={\Sigma }_{i=1}^N\Vert y_i-\widehat{y_i}{\Vert }_2^2$$
最小即可。虽然在很多场合都会用MSE均方误差来做损失函数，但是为了方便手动计算梯度，就不用MSE了，两者回归出来的最优值是一样的。

设
$W=\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right]$,$Z=\left[\begin{array}{c}1\\ x\\ x^2\end{array}\right]$,则$f(x)$可以写为$f(x)=W^{T}Z$

整体的梯度下降步骤：

1. 初始化权重W
   直接随机初始化
2. 计算拟合损失
   
   对每一组数据$z_i$, $y_i$ in (Z,Y)，$$los{s}_i=(y_i-\widehat{y_i}{)}^2=(y_i-W^T{z}_i{)}^2=(y_i-(w_1{z}_{i1}+w_2{z}_{i2}+w_3{z}_{i3}){)}^2$$

$los{s}_i$对$W$的梯度就是$\nabla =[\begin{array}{c}-2(y_i-(w_1{z}_{i1}+w_2{z}_{i2}+w_3{z}_{i3})z_{i1}\\ -2(y_i-(w_1{z}_{i1}\end{array}$

用梯度下降做点小实验

赶在国庆回家前做点小实验==

利用梯度下降法去拟合任意你想拟合的东西，哈哈

自己想出来的曲线：

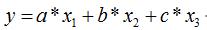
 目标函数：

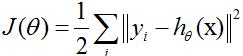
其中：

，

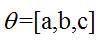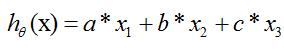
然后计算迭代式：

其中：

k表示第k次迭代，

 

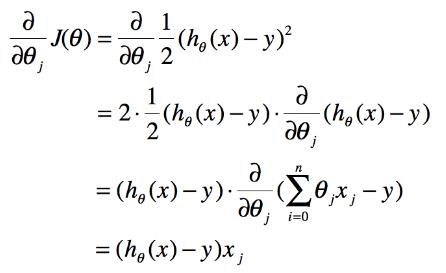
 至此，有了梯度方向就可以计算啦，附上c++代码：

#include<iostream>
#include<vector>
#include<ctime>
using namespace std;

int main() {
	//产生数据
	srand(time(NULL));
	vector<vector<double>> x(5,vector<double>(3,0.0));
	for (int i = 0; i < 5; i++) {
		for (int j = 0; j < 3; j++) {
			x[i][j] = rand() % 10+1;
			//cout << x[i][j] << " ";
		}
		//cout << ",";
	}
	//double *y = new double[5];
	double y[5];
	for (int i = 0; i < 5; i++) {
		 y[i] = 3 * x[i][0] + 5 * x[i][1] - 7 * x[i][2] + double((rand() % 7)) / 10;
		// cout << y[i] << endl;
	}
	double a=0.0,b=0.0,c=0.0,
		aa=0.0,bb=0.0,cc=0.0;
	double diff;
	double error=0,error1=0;
	int itertornum = 0;//记录迭代次数
	while (1) {
		itertornum++;
		for (int i = 0; i < 5; i++) {
			cout << "第"<<itertornum<<"次迭代："<<aa << "," << bb << "," << cc << "," << endl;
			diff = y[i] - (a*x[i][0] + b*x[i][1] + c*x[i][2]);
			aa = aa + 0.001*diff*x[i][0];
			bb = bb + 0.001*diff*x[i][1];
			cc = cc + 0.001*diff*x[i][2];
		}
		a = aa; b = bb; c = cc;//更新状态量
		error = 0;
		for (int i = 0; i < 5; i++) {
			error += 0.5*(pow(y[i] - (a*x[i][0] + b*x[i][1] + c*x[i][2]), 2));
		}
		if (abs(error - error1) < 1e-5) {
			break;
		}
		else {
			error1 = error;
		}
	}
	cout << "最终结果是：" << a <<","<< b<<"," << c<<endl;
	system("pause");
	return 0;
}