数据在内存中的存储

Posted 2022-11-28 zsQgqdsd1002

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据在内存中的存储相关的知识，希望对你有一定的参考价值。

数据在内存中的存储

前言
一.原码，反码，补码
二、整型数据在内存中的存储
三、浮点型数据在内存中的存储
总结

前言

我们知道，创建一个变量就要在内存中开辟一块空间，开辟的这块空间的大小是取决于你数据类型的，变量又可以分为很多类，有整型变量，有浮点型变量，有字符型变量等等，我们今天所要分析的就是整型和浮点型在内存中的存储方式。

提示：以下是本篇文章正文内容，下面案例可供参考

一.原码，反码，补码

我们首先来了解一下原码，反码，补码三个概念。他们三个的表示方法有两个共同的地方，就是都是分为符号位和数值位两方面。符号位都是用0来表示正数，1来表示负数。而数值位方面则是各有不同，我们下来一一介绍。

原码就是数字本身的样子，即就是把一个数字分解成32位得到的数值。对于正数而言，这32位都是数值位，而对于负数而言，第一位是符号位1，其余的也不是数值位，这些我们一会会讲到。

反码就是在原码的基础上，符号位不变，其余位全部取反得到的结果。

补码则是在反码的基础之上加1就可以了，负数在计算机中的存储通常是以补码形式存在的。而这也就是为什么负数的原码符号位之后不是数值位的原因。

二、整型数据在内存中的存储

我们知道，数据在计算机中的存储都是由二进制来完成的，对于整型变量来说，一个数字可以被分解为32位，由32个0和1组成，其可以表示的范围在无符号的情况下大概是0~42亿9千万，在有符号的情况下则大概是-21亿~21亿。

需要注意的是，对于正数而言，它的原码，反码，补码都相同；而对于负数而言，它的原码，反码，补码就需要以上面所讲述的形式进行换算，对于整型数据来说，它们在计算机中的存储都是用补码的形式进行存储的。为什么呢？

因为使用补码的话可以将符号位和数值位统一进行处理，由于我们的计算机智能进行加法运算，所以用这种形式来储存数据在计算起来也会非常的方便。我们来举个例子：

#include<stdio.h>
int main()

	int a = 1;
	int b = 1;
	printf("%d", a - b);
	return 0;

前面说到计算机是只有加法没有减法的，所以程序中虽然写的是a - b但是在实际的运算中计算机所运算的会是a + (-b)，那么计算机会如何进行计算呢？我们一起来看一下：

首先计算机会拿到1的原码，因为正数的原反补都相同，即此时把1转为：

				0000 0000 0000 0000 0000 0000 0000 0001

其次计算机会拿到-1的原码，但是由于数据在计算机中的存储都是以补码形式存在的，所以这个时候计算机会先拿到其反码在将其转为补码形式，即就是：

			1000 0000 0000 0000 0000 0000 0000 0001
取反--->    1111 1111 1111 1111 1111 1111 1111 1110
取补--->    1111 1111 1111 1111 1111 1111 1111 1111

得到了-1的补码之后，将-1的补码与1的补码进行相加操作：

			0000 0000 0000 0000 0000 0000 0000 0001
	+		1111 1111 1111 1111 1111 1111 1111 1111
	=	   10000 0000 0000 0000 0000 0000 0000 0000

由于int类型只能存储32位，那么现在1的位置处于第33位，舍弃之，最后得到的就是32位0，也就是数字0

三、浮点型数据在内存中的存储

1.思考

我们来看这样一段代码：

int main()

	int a = 1;
	float* p = (float*)&a;//将a强制转换为float类型
	printf("%d\\n", a);
	printf("%f\\n", *p);
	return 0;

此时程序会输出什么？第一行是1，第二行是1.000000吗？我们一个编译执行来看一下：

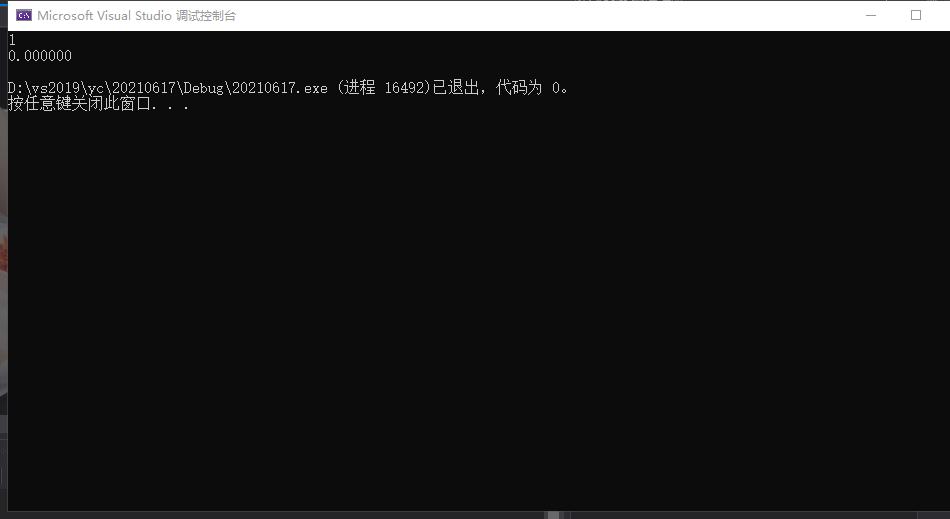
这是为什么呢？我们下面来慢慢介绍：

2.答疑解惑

根据国际标准IEEE(电气和电子工程协会)754，任意一个二进制浮点数V可以表示成下面的形式：

(-1)^S*M*2^E
其中(-1)^s表示符号位，当S = 0，V为正数；当S = 1，V为负数。
M表示有效数字，这个数字大于等于1且小于2。
2^E表示数位

我们举例来说，比方说十进制的6.0，写成二进制位就是110.0相当于1.10 * 2^2。那么我们根据上面的格式可以得到
S = 0，M = 1.10，E = 2

同样的，十进制中的-6.0，写成二进制位就是-110.0相当于-1.10*2^2，根据上面的格式相可以得到
S = 1， M = 1.10， E = 2

根据IEEE 754的规定：
对于32位的浮点数而言，最高位的为符号位，接着的8位数字是指数位，最后的23位则为有效数字

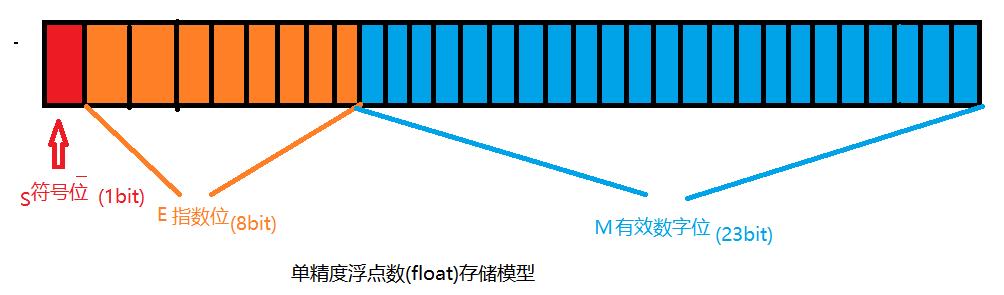
如图所示，这就是单精度浮点数的各个位详情。

那么对于双精度浮点数来说，大体也是这个规律，只是我们知道双精度浮点数的大小为8个字节，所以在这个地方S，M，E就有一点点不同的地方了，此时的S仍旧是第一位表示符号，中间的E则会变成11位，而最后的52位则都是有效数字位M。

3.M和E

我们下面来说一说M和E，IEEE 754在对M和E这方面还有一些特殊的规定，我们来先说一说M：

(1)M

我们前面提到过M的取值范围是1到2之间，也就是说M的书写形式可以写为1.xxxxxx，其中后面的六个x便代表的是小数部分。根据规定，在计算机内部保存M的时候，默认M的第一位是1，所以可以被舍去然后只保留后面六个x的部分。我们比方说是1.01，只保存01这个部分，等到读取的时候再把这个1拿出来，这样做可以节省一位有效数字，以float类型的数据为例，M只能保存23位有效数字，而当我们省去这个1的时候，他就可以保留24位有效数字。

(2)E

下面我们再来介绍一下指数位的E:

E的存储

首先我们要知道指数位的E它的类型是unsigned int，即就是无符号的整数类型，我们知道E是8位或者11位，这取决于数据类型是float类型还是double类型。如果是float类型，它能表示的范围就是0~255之间；如果是double类型，那么它能表示的范围就是0~2047。但是我们知道，指数位是可以为负数的，所以在IEEE 754的规定下，存入内存时的E需要加上一个中间值，对于8位的E来说这个中间值是127，而对于11位的E来说这个中间值则是1023。我们来举个例子：

例如2^10，我们知道E的值为10，如果以float类型去存储它，存入E的时候要存入的不能是10的二进制00000110，而是10 + 127 = 137，即就是10000101