LeetCode 211.添加与搜索单词, swift
Posted 想名真难
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode 211.添加与搜索单词, swift相关的知识,希望对你有一定的参考价值。
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary() 初始化词典对象
void addWord(word) 将 word 添加到数据结构中,之后可以对它进行匹配
bool search(word) 如果数据结构中存在字符串与 word 匹配,则返回 true ;否则,返回 false 。word 中可能包含一些 '.' ,每个 . 都可以表示任何一个字母。
1 <= word.length <= 25
addWord 中的 word 由小写英文字母组成
search 中的 word 由 '.' 或小写英文字母组成
最多调用 10^4 次 addWord 和 search
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // 返回 False
wordDictionary.search("bad"); // 返回 True
wordDictionary.search(".ad"); // 返回 True
wordDictionary.search("b.."); // 返回 True
犹豫不决, 没有思路的时候就先想想暴力法,
- addWord的时候把单词加入到一个集合中,
- 到搜索的时候, 如果入参的单词含有 "." , 那就把这个 "." 换成 "a ~ z"的所有字母, 枚举出所有可能的组合, 然后拿枚举出的组合和单词集合进行比对
- 如果这个组合中有和集合中重复的元素, 那就说明存在, 返回ture
- 如果集合中和枚举出的所有情况都没有交集, 说明不存在, 返回false
这个是2种暴力法的实现, 时间复杂度取决于点的数量, 如果有n个 ".", 那就是O(26^n), 到LeetCode上运行 果然出现了超时,
// 暴力法1
class WordDictionary
var dictionarySet = Set<String>.init()
init()
func addWord(_ word: String)
dictionarySet.update(with: word)
func search(_ word: String) -> Bool
// 暴力法,把work所有的情况枚举出来放到一个集合中
let wordSet = changeWorkToSet(word: word)
// 取2个集合的并集, 结果为空, 说明不包含; 结果有值, 说明存在
let resultSet = dictionarySet.intersection(wordSet)
if resultSet.isEmpty
return false
else
return true
func changeWorkToSet(word : String) -> Set<String>
// 包含点,把一个点换成具体的字符,然后递归调用自己,直到所有的.都消失
if word.contains(".")
var set = Set<String>.init()
let startIndex = word.firstIndex(of: ".")!
let endIndex = word.index(startIndex, offsetBy: 1)
let alphabet: [String] = ["a", "b", "c", "d", "e", "f",
"g", "h", "i", "j", "k", "l",
"m", "n", "o", "p", "q", "r",
"s", "t", "u", "v", "w", "x",
"y", "z"]
for replaceChar in alphabet
var newWord = word
newWord.replaceSubrange(startIndex..<endIndex, with: replaceChar)
let resultSet = changeWorkToSet(word: newWord)
for resultWord in resultSet
set.update(with: resultWord)
return set
else
// 不包含点, 直接返回一个set,set中只有一个元素
return Set.init(arrayLiteral: word)
// 暴力法2, 计算出一个结果就触发回调, 没有必要把所有情况都枚举出来
class WordDictionary
var dictionarySet = Set<String>.init()
// 应不应该继续遍历, 每一个新的查询开始的时候设置为true
var shouldContinue = true
init()
func addWord(_ word: String)
dictionarySet.update(with: word)
func search(_ word: String) -> Bool
shouldContinue = true
var result = false
// 暴力法,把work所有的情况枚举出来进行回调判断
changeWorkToComplete(word: word) resultString in
if self.dictionarySet.contains(resultString)
result = true
self.shouldContinue = false
return result
func changeWorkToComplete(word : String, complete: @escaping (String) -> Void)
// 只要找到一个,结束遍历
if !shouldContinue
return
// 包含点,把一个点换成具体的字符,然后递归调用自己,直到所有的.都消失
if word.contains(".")
let startIndex = word.firstIndex(of: ".")!
let endIndex = word.index(startIndex, offsetBy: 1)
let alphabet: [String] = ["a", "b", "c", "d", "e", "f",
"g", "h", "i", "j", "k", "l",
"m", "n", "o", "p", "q", "r",
"s", "t", "u", "v", "w", "x",
"y", "z"]
for replaceChar in alphabet
var newWord = word
newWord.replaceSubrange(startIndex..<endIndex, with: replaceChar)
changeWorkToComplete(word: newWord, complete: complete)
else
// 不包含点了, 直接回调
complete(word)
官方解法, 从二叉树说起
前缀树(Trie,字典树),也是一种树。为了理解前缀树,我们先从「二叉树」说起。
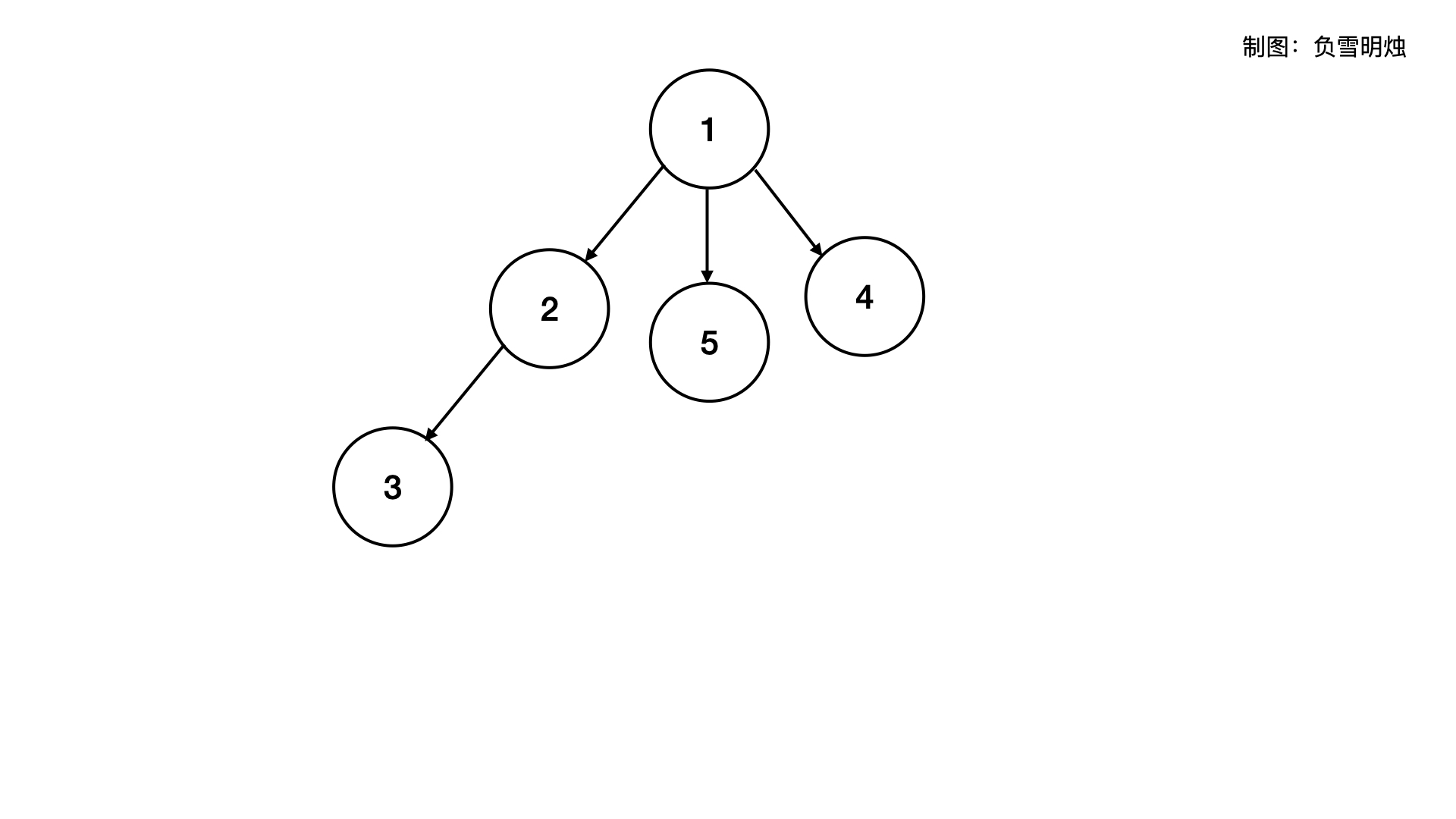
常见的二叉树结构是下面这样的:
class TreeNode
int val;
TreeNode* left;
TreeNode* right;
可以看到一个树的节点包含了三个元素:该节点本身的值,左子树的指针,右子树的指针。
二叉树可视化是下面这样的:
二叉树的每个节点只有两个孩子,那如果每个节点可以有多个孩子呢?这就形成了「多叉树」。多叉树的子节点数目一般不是固定的,所以会用变长数组来保存所有的子节点的指针。多叉树的结构是下面这样:
class TreeNode
int val;
Array<TreeNode*> children;
多叉树可视化是下面这样:
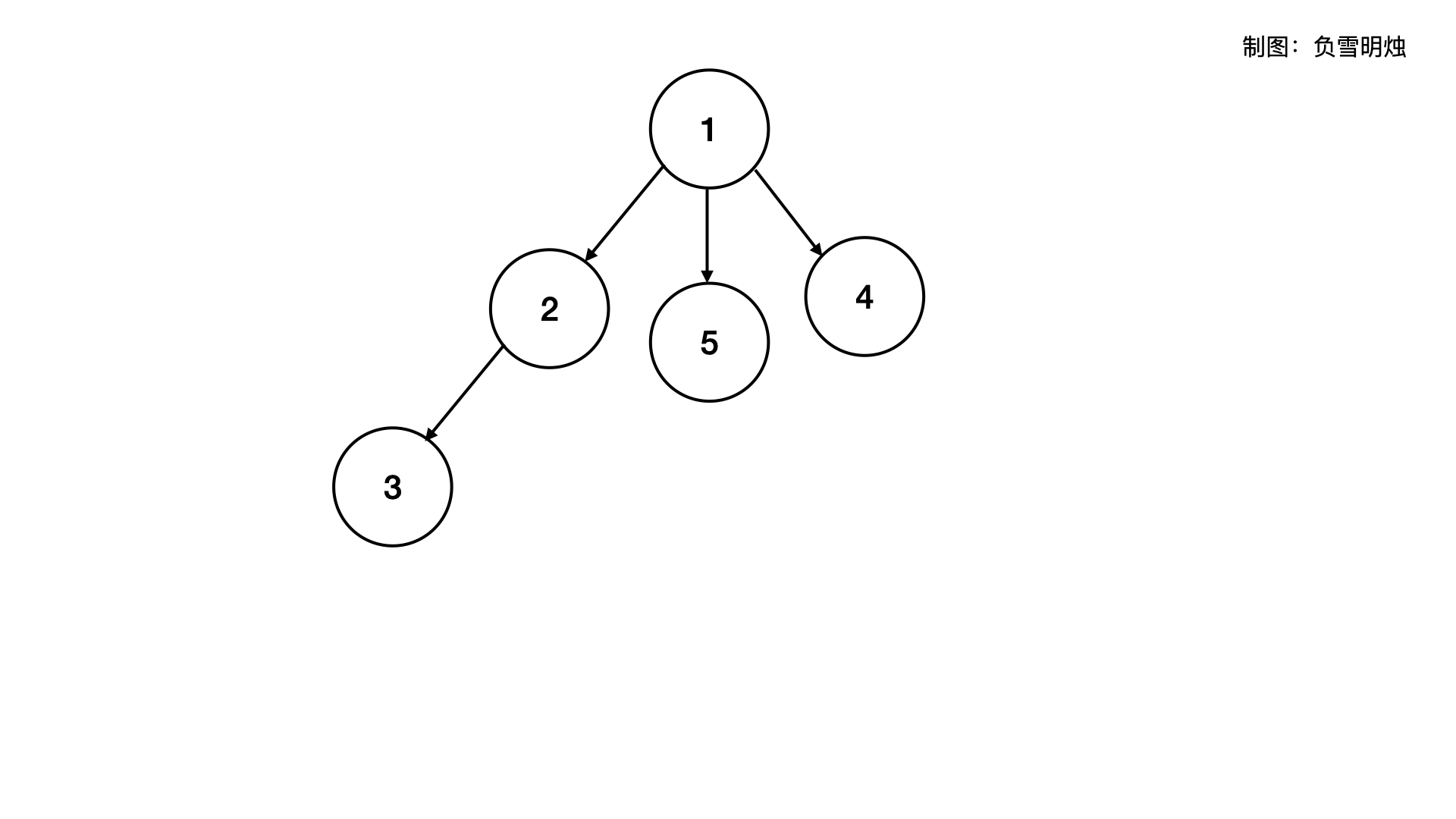
对于普通的多叉树,每个节点的所有子节点可能是没有任何规律的。而本题讨论的「前缀树」就是每个节点的 children 有规律的多叉树。
前缀树
「前缀树」是一种特殊的多叉树,它的 TrieNode 中 chidren 是一个大小为 26 的一维数组(当输入只有小写字符),分别对应了26个英文字符 'a' ~ 'z',也就是说形成了一棵「26 叉树」。
前缀树的结构可以定义为下面这样:
class WordNode
// 父节点, 为了方便调试溯源
var superNode : WordNode? = nil
// 子节点数组
var childNodeArray : [WordNode] = [WordNode]()
// 节点的深度
var deep = 0
// 节点对应的字母
var key = ""
// 标记为路径中的某个点
var isPath = 0
// 标记为最后一个字母
var isEnd = 0
TrieNode 里面主要存储了两个信息, 其他都是辅助信息:
- children 是该节点的所有子节点。
- isEnd 表示从根节点到当前节点为止,该路径是否形成了一个有效的字符串。
构建
在构建前缀树的时候,按照下面的方法:
- 根节点不保存任何信息;
- 关键词放到「前缀树」时,需要把它拆成各个字符,每个字符按照其在 'a' ~ 'z' 的序号,放在 chidren 对应的位置里面。下一个字符是当前字符的子节点。
- 一个输入字符串构建「前缀树」结束的时候,需要把该节点的 isEnd 标记为 true,说明从根节点到当前节点的路径,构成了一个关键词。
下面是一棵「前缀树」,其中保存了 "am", "an", "as", "b", "c", "cv" 这些关键词。图中红色表示 isWord 为 true。
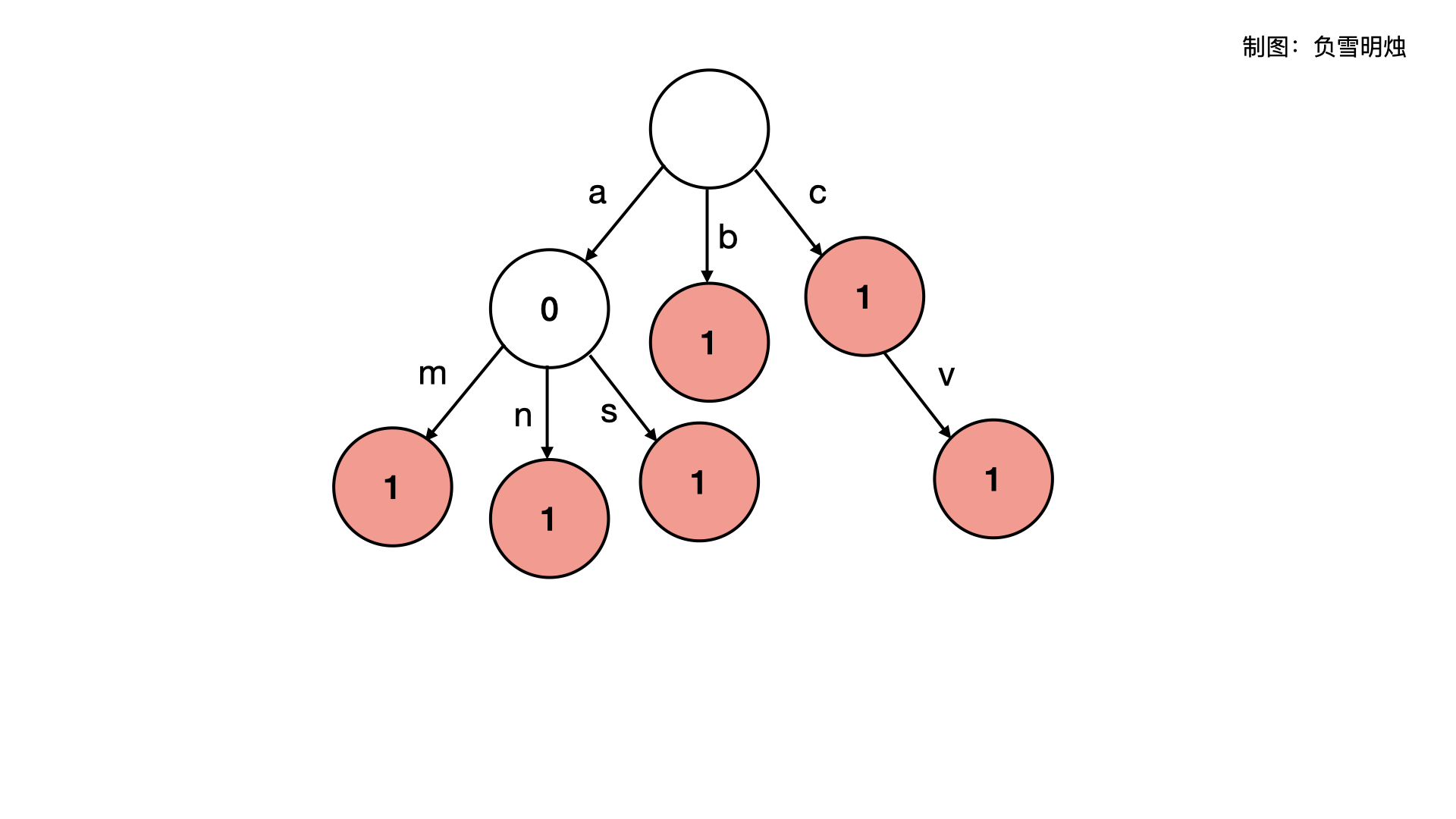
看下面这个图的时候需要注意:
所有以相同字符开头的字符串,会聚合到同一个子树上。比如 "am", "an", "as" ;
并不一定是到达叶子节点才形成了一个关键词,只要 isEnd 为 true,那么从根节点到当前节点的路径就是关键词。比如 "c", "cv" ;
前缀树是根据 字符在 children 中的位置确定子树。树中每个节点存储的 isEnd,表示从根节点到当前节点的路径是否构成了一个关键词。
查询
在判断一个关键词是否在「前缀树」中时,需要依次遍历该关键词所有字符,在前缀树中找出这条路径。可能出现三种情况:
- 在寻找路径的过程中,发现到某个位置路径断了。比如在上面的前缀树图中寻找 "d" 或者 "ar" 或者 "any" ,由于树中没有构建对应的节点,那么就查找不到这些关键词;
- 找到了这条路径,但是最后一个节点的 isEnd 为 false。这也说明没有该关键词。比如在上面的前缀树图中寻找 "a" ;
- 找到了这条路径,并且最后一个节点的 isEnd 为 true。这说明前缀树存储了这个关键词,比如上面前缀树图中的 "am" , "cv" 等。
上面说了这么多前缀树,那前缀树有什么用呢?其实我们生活中就有应用。
- 比如我们常见的电话拨号键盘,当我们输入一些数字的时候,后面会自动提示以我们的输入数字为开头的所有号码。
- 比如我们的英文输入法,当我们输入半个单词的时候,输入法上面会自动联想和补全后面可能的单词。
- 再比如在搜索框搜索的时候,输入"a",后面会联想到 已a为起始的联想词 。
本题是前缀树的变种: '.' 可以表示任何一个小写字符。
在匹配的过程中,如果遇到了 '.' ,则需要对当前节点的所有子树都进行遍历,只要有任何一个子树能最终匹配完成,那么就代表能匹配完成。
还有一个优化, 从暴力法里保留下来 , 如果需要匹配的单词不存在 ".", 那就内部在添加操作时同时准备一份set集合, 需要搜索时直接和set中的元素进行匹配即可.
import Foundation
let alphabet: [String] = ["a", "b", "c", "d", "e", "f",
"g", "h", "i", "j", "k", "l",
"m", "n", "o", "p", "q", "r",
"s", "t", "u", "v", "w", "x",
"y", "z"]
let alphabetIndexDic: [Character:Int] = ["a":0, "b":1, "c":2, "d":3, "e":4, "f":5,
"g":6, "h":7, "i":8, "j":9, "k":10, "l":11,
"m":12, "n":13, "o":14, "p":15, "q":16, "r":17,
"s":18, "t":19, "u":20, "v":21, "w":22, "x":23,
"y":24, "z":25]
class WordDictionary
var rootNode = WordNode()
var maxDeep = 0
var searchFinish = false
var set = Set<String>()
init()
func addWord(_ word: String)
// 对不存在"."的单词单独判断
set.update(with: word)
var currentWordNode = rootNode
for oneChar in word
let index = changeStringToIndex(oneChar: oneChar)
currentWordNode.createChildNodeIfNeed()
currentWordNode.isPath = 1
currentWordNode = currentWordNode.childNodeArray[index]
maxDeep = max(maxDeep, word.count)
currentWordNode.isEnd = 1
currentWordNode.deep = word.count
// 找出"a", "b", "c" ... 对应的数组下表, 这点swift特别不方便
func changeStringToIndex(oneChar : Character) -> Int
return alphabetIndexDic[oneChar]!
func search(_ word: String) -> Bool
// 最大长度小于单词长度, 肯定不存在
if self.maxDeep < word.count
return false
var isMatch = false
if word.contains(".")
searchFinish = false
p_seach(word, startNode: rootNode) [weak self] resultNode in
// print(resultNode.description())
if resultNode.isEnd == 1 && resultNode.deep == word.count
self?.searchFinish = true
isMatch = true
return isMatch
else
isMatch = set.contains(word)
return isMatch
func p_seach(_ word: String, startNode : WordNode, complete: @escaping (WordNode) -> Void) -> WordNode
if searchFinish
return startNode
var currentWordNode = startNode
for oneChar in word
if oneChar == "."
// 那就是取出所有带有路径的子节点, 然后递归调用自己
let pathArray = currentWordNode.getNodeWithPath()
let startIndex = word.firstIndex(of: ".")!
let endIndex = word.index(startIndex, offsetBy: 1)
var newWord = word
newWord = newWord.substring(from: endIndex)
for childNode in pathArray
if searchFinish
return startNode
currentWordNode = p_seach(newWord, startNode: childNode, complete: complete)
else
// 取出正常的字母,沿着字母继续向下
if currentWordNode.childNodeArray.count > 0
let index = changeStringToIndex(oneChar: oneChar)
currentWordNode = currentWordNode.childNodeArray[index]
// 当前节点不存在路径
if currentWordNode.isPath == 0
break
complete(currentWordNode)
return currentWordNode
class WordNode
var superNode : WordNode? = nil
var childNodeArray : [WordNode] = [WordNode]()
var deep = 0
var key = ""
// 比如 "ba", "bad", 第二个节点a 是bad路径中的点, 也是ba的结束点
// 标记为路径中的某个点
var isPath = 0
// 标记为结束点
var isEnd = 0
func createChildNodeIfNeed()
if self.childNodeArray.isEmpty
for key in alphabet
let childNode = WordNode()
childNode.key = key
childNode.superNode = self
self.childNodeArray.append(childNode)
func getNodeWithPath() -> [WordNode]
let result = childNodeArray.filter childNode in
childNode.isPath == 1 || childNode.isEnd == 1
return result
func description() -> String
var startNode = self
var result = self.key
while startNode.superNode != nil
result.append(contentsOf: startNode.superNode!.key)
startNode = startNode.superNode!
return String(result.reversed())
官方的题解也是这样的写法, 但是swift按照同样的思路写出来就是超时, 😭😭😭, 时间复杂度为O(m^n), 这里的m为子节点中isPath+isEnd的数量和, n还是'.'的数量
和暴力法相比, 底数不是无脑的取所有字母, 而是使用曾经作为路径的节点, 最差的情况就是所有字母都作为路径出现过, 那就和暴力法复杂度一致,
还有一种办法, 把'.'转成对应的字母总是要面对最多26种情况, 但是也可以返过来, 我把字母转成'.', 这个面临的情况就少很多了, 需要搜索时, 取出同长度的所有单词, 然后把每个单词同位置的字母换成'.', 这样的话,至少不是指数级的复杂度,
- 构造一个字典, key为单词的长度, value为一个数组, 数组中存放的是字符, 比如传入bad, mad, pad, abc, 就可以构造出这样一个字典 3: ["bad","mad","pad","abc"] ,
- 当传入的word为 ".ad"时, 取出和word同长度的所有字符, ["bad","mad","pad","abc"]
- 对所有字符进行处理, 替换同等位置的字符为 ".", 处理后变成 [".ad",".ad",".ad",".bc"],
- 处理后的集合和 word进行比对, 存在一致的, 说明匹配成功; 不存在一致, 说明匹配不成功;
class WordDictionary
// 记录单词的最大长度
var maxDeep = 0
// 记录每个单词, 搜索的时候,如果是不包含'.', 直接使用set进行匹配
var set = Set<String>()
// 单词长度作为key, 所有同长度单词组成一个数组
var countDic : [Int : [String]] = [Int : [String]]()
init()
func addWord(_ word: String)
maxDeep = max(maxDeep, word.count)
// 更新set内容
set.update(with: word)
// 构造字典,
var array = countDic[word.count]
if array == nil
array = [String]()
array?.append(word)
countDic[word.count] = array
func search(_ word: String) -> Bool
if self.maxDeep < word.count
return false
var isMatch = false
if word.contains(".")
let tmpArray = countDic[word.count]
if let array = tmpArray
// 替换数组中的字母,进行匹配
isMatch = match(array: array, word: word)
return isMatch
else
isMatch = set.contains(word)
return isMatch
func match(array : [String], word : String) -> Bool
// 取出所有'.'所在的range,进行替换
var rangeArray = [Range<String.Index>]()
for (index,oneChar) in word.enumerated()
if oneChar == "."
let startIndex = word.index(word.startIndex, offsetBy: index)
let endIndex = word.index(startIndex, offsetBy: 1)
rangeArray.append(startIndex..<endIndex)
// 从数组中匹配,把对应位置的字母换成 '.', 然后和word进行匹配
for key in array
var replaceKey = key
for range in rangeArray
replaceKey.replaceSubrange(range, with: ".")
if replaceKey == word
return true
return false

这种算法的时间复杂度为,O(m*n), m为同长度的单词个数, n为搜索中'.'的数量. 比起前2种来说, 效率提升巨大.
总共有29个测试用例
- 性能最好的是第3种, 能通过所有用例, 并且不超时, 在swift中超过100%
- 第2种前缀树算法, 通过18个测试用例,然后触发超时,
- 暴力法, 通过9个测试用例然后触发超时

最后吐槽下, 第二种算法按照官方的题解思路写出来, 性能差异巨大, 不知道是swift本身的问题, 还是LeetCode上用的黑苹果.
- 使用java执行需要674ms,
- 使用c#写同样思路的代码, 需要1286ms,
- 而swift写就是超时,超过了4000ms, 比java差了6倍以上, 比c#的效率差了3倍以上.
以上是关于LeetCode 211.添加与搜索单词, swift的主要内容,如果未能解决你的问题,请参考以下文章