ikd-Tree:增量KD树在机器人中的应用
Posted Being_young
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ikd-Tree:增量KD树在机器人中的应用相关的知识,希望对你有一定的参考价值。
文章:ikd-Tree: An Incremental K-D Tree for Robotic Applications
作者:Yixi Cai, Wei Xu and Fu Zhang
编译:点云PCL
代码:https://github.com/hku-mars/ikd-Tree
本文仅做学术分享,如有侵权,请联系删除。欢迎各位加入免费知识星球,获取PDF论文,欢迎转发朋友圈。内容如有错误欢迎评论留言,未经作者允许请勿转载,欢迎各位同学积极分享和交流。
公众号致力于分享点云处理,SLAM,三维视觉,高精地图相关的文章与技术,欢迎各位加入我们,一起每交流一起进步,有兴趣的可联系微信:920177957。本文来自点云PCL博主的分享,未经作者允许请勿转载,欢迎各位同学积极分享和交流。
摘要
本文提出ikd树,一种有效的动态空间划分的数据结构,ikd树只使用加入的数据点来增量的更新k-d树,比现有静态k-d树的计算时间少很多,除了逐点操作外,ikd树还支持一些功能,例如在机器人应用中实际有用的逐个区域操作和向下采样,与增量操作(即插入、重新插入和删除)并行,ikd-Tree主动监视树结构并重新平衡树结构,从而在后期实现高效的最近点搜索,ikd tree经过了精心设计,支持多线程并行计算,以最大限度地提高整体效率,我们在理论和实际实验中验证了ikd tree,在理论层面上,给出了完整的时间复杂度分析,证明了该方法的高效性, 在实验层面,在激光雷达惯性里程计和地图应用中,对随机数据集和真实世界的激光雷达点数据进行了ikd树测试,在所有测试中,ikd tree只消耗静态k-d tree中运行时间的4%。
介绍
K-Dimensional Tree(K-D Tree)是一种高效的数据结构,用于组织多维点的数据[1],从而能够快速搜索最近邻数据,这是各种机器人应用中广泛需要的一种基本数据结构,例如,在激光雷达里程计和地图绘制中,基于k-d树的最近点搜索对于将新激光雷达扫描中的点与其在地图(或上一次扫描)中的对应点匹配至关重要。最近邻点搜索在点云上快速障碍物碰撞检查的运动规划中也很重要。机器人应用中常用的k-d树结构是“静态”的,其中树是使用所有点从头开始构建的,这与实际机器人应用中通常按顺序获取数据的事实相矛盾。在这种情况下,通过从头开始重新构建整个数据树,将新数据框架合并到现有数据框架中通常是非常低效和耗时的。因此,k-d树通常以低频率更新,或者仅在新点上重建,为了适应顺序数据采集的性质,更自然的k-d树设计是使用新采集的数据在本地更新(即插入和删除)现有树,本地更新将有效地消除重建整个树时的冗余操作,并节省大量计算。当新数据比树中现有数据小得多时,这种动态k-d树尤其有价值的。
然而,适合机器人应用的动态k-d树带来了几个挑战:
1)它不仅要支持插入和删除等高效点操作,还应支持点云下采样等空间操作;
2) 在大量的点或空间操作之后,它很容易变得不平衡,从而降低点查询的效率。因此,需要重建以重新平衡树。
3) 重建应足够有效,以实现实时机器人应用程序。
在本文中,我们提出了一种称为ikd树的动态k-d树结构,该结构只使用新的点来构建和增量更新k-d树,同时将它们向下采样到所需的分辨率。它支持增量操作,包括插入、重新插入和删除单个点(即逐点)或一盒点。树通过部分重建自动重新平衡,为了保持高效的实时树更新,ikd Tree在必要时将树重新构建分离为两个并行线程。本文还提供了所有树更新的完整时间复杂性分析,包括增量操作和重新平衡,在激光雷达惯性建图应用中,通过随机数据和真实点云的验证,ikd树的时间复杂度大大降低,ikd树在Github1是开源的。
图1示出了从三维视图在树上的增量更新和重新平衡。
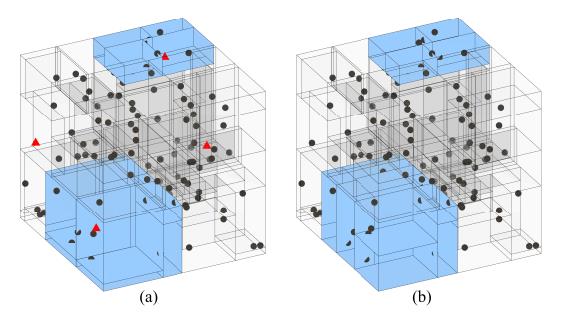
图1:增量k-d树更新和重新平衡的图示,(a) :要插入的现有k-d树(黑点)和新点(红色三角形),蓝色立方体表示需要重新平衡的空间(即分支)。(b) :插入点和树重新平衡后的k-d树,蓝色立方体表示重新平衡后的空间,而其余多数树不变
主要内容
这里将描述如何在ikd树中设计、构建和更新增量k-d树,以允许增量操作(例如插入、重新插入和删除)和动态重新平衡。
A、 数据结构
ikd树中树节点的属性如数据结构1所示

第2-4行是标准k-d树的常见属性,属性leftson和rightson分别是指向其左和右子节点的指针,点信息(例如点坐标、强度)存储在点中,由于一个点对应k-d树上的一个节点,我们将互换使用点和节点,分割轴记录在轴中。第5-7行是为增量更新设计的新属性。
B、 构建增量K-D树
构建增量K-D树与构建静态K-D树类似,只是为增量更新维护额外信息,整个算法如算法1所示:

给定一个点阵列V,首先按协方差最大的分割轴对点进行排序(第4-5行),然后中值点保存到新树节点T的点(第6-7行),中位数下方和上方的点分别传递给T的左和右子节点,用于递归构建(第9-10行),第11-12行中的LazyLabelInit和Pullup更新了增量更新所需的所有属性。
C、 增量更新
增量更新指的是增量操作,随后进行动态重新平衡。增量操作包括向k-D树插入、删除和重新插入新点,具体而言,插入操作将一个新点(即节点)附加到k-d树,在删除操作中,我们使用了延迟删除策略,也就是说,不会立即从树中删除点,而只会通过将属性deleted设置为true来标记为“deleted”(已删除)。如果已删除以T为根的子树上的所有节点,则T的属性treedeleted设置为true,因此,删除的属性和树删除的属性称为惰性标签。如果标记为“已删除”但未删除的点稍后插入到树中,则称为“重新插入”,只需将删除的属性设置回false即可有效地实现。否则,标记为“已删除”的点将在重建过程中从树中删除,我们的增量更新支持两种类型:点式更新和框式更新,逐点更新在树上插入、删除或重新插入单个点,而逐框更新在与数据坐标轴对齐的给定框中插入、删除或重新插入所有点,框式更新可能需要删除或重新插入以T为根的整个子树。在这种情况下,递归更新T的所有子节点的已删除和已删除的懒惰标签仍然是低效的。为了解决这个问题,我们使用了进一步的延迟策略来更新子节点的延迟标签。
1) Pushdown和Pullup:两个支持函数Pushdown和Pullup用于更新树节点T上的属性,当属性Pushdown为true时,Pushdown函数将标签deleted、tree deleted和T的Pushdown复制到其子代(但不复制其他子代)。Pullup函数将以T为根的子树的信息汇总到节点T的以下属性:tree size保存子树上所有节点的数量,invalid num保存子树上标记为“已删除”的节点数量,range汇总子树上沿坐标轴的所有点的范围,其中k是点尺寸。
2) 逐点更新:增量k-d树上的逐点更新以递归方式实现,类似于k-d树,对于逐点插入,该算法从根节点递归向下搜索,并将新点在分割轴上的坐标与存储在树节点上的点进行比较,直到找到一个叶节点来附加新的树节点,对于点P的删除或重新插入,该算法会找到存储点P的树节点,并修改删除的属性。更多详细信息可以在我们的Github中找到。
3) 框式更新:框式插入是通过在增量k-d树中逐个插入新点来实现的,其他框式更新(框式删除和重新插入)是利用属性range中的范围信息实现的,该属性range形成一个框式CT,并在树节点上使用惰性标签。伪代码如算法2所示。

4)下采样:我们的ikd树进一步支持下采样,如算法3所述,对于给定的点P和下采样分辨率L,该算法将空间均匀地划分为长度为L的立方体,然后找到包含点P的长方体CD(第1行),该算法只保留最靠近CD中心的点(第2行),这是通过首先在k-d树上搜索CD中包含的所有点,并将它们与新点P(第3-4行)一起存储在点阵列V中来实现的,通过比较V中每个点到中心Pcenter(第5行)的距离,获得最近点Pnearest。然后删除CD中的现有点(第6行),然后将最近的点Pnearest插入到k-d树(第7行),框式搜索的实现类似于框式删除和重新插入。

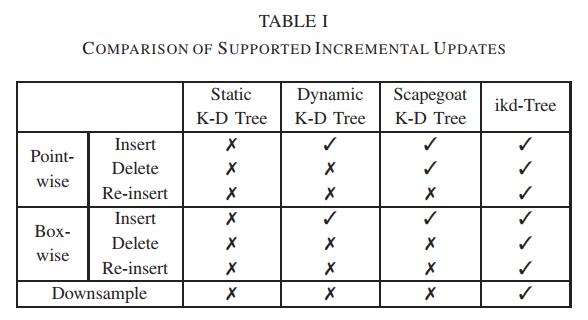
图2中示出了下采样的示例。总之,表I显示了静态k-d树、动态k-d树、替代k-d树和我们的ikd树上支持的增量更新的比较。

图2:点云下采样(a) :下采样前的点云。(b) :向下采样后的点云
D、 重新平衡ikd树
主动监视增量k-D树的平衡属性,并通过部分重建动态地重新平衡它, 平衡准则由两个子准则组成:α-平衡准则和α-删除准则。

图3:重建不平衡子树
重建算法如算法4所示,将要在线程中重建的子树表示为T,将其根节点表示为T,第二个线程将锁定所有增量更新(即点插入、重新插入和删除),但不会锁定此子树上的查询(第2行)。然后,第二个线程将子树T中包含的所有有效点复制到点数组V中,同时保持原始子树不变,以便在重建过程中进行可能的查询(第3行)。展开后,将解锁子树,以便主线程进一步请求增量更新(第4行)。这些请求将被挂起并记录在名为operation logger的队列中。一旦第二个线程完成从点阵列V(第5行)构建新的平衡k-d树T',记录的更新请求将通过函数增量更新(第6-8行)在平衡子树T′上执行,其中并行重建选项设置为false(因为它已经在第二个线程中)。在处理完所有挂起的请求后,该算法将节点T锁定在增量更新和查询中,并将其替换为新的节点T′(第9-12行)。最后,该算法释放原始子树的内存(第13行)。请注意,LockUpdates不会阻止查询,查询可以在主线程中并行执行。相反,LockAll会阻止包括查询在内的所有访问,但它完成得非常快(即只有一条指令),允许在主线程中及时查询。LockUpdates和LockAll函数是通过互斥(互斥)实现的。

E、 K-最近邻搜索
增量K-d树上的最近邻搜索是精确的最近邻搜索,而不是近似的最近邻搜索,在搜索以节点T为根的子树以传递其惰性标签之前,应用函数Pushdown,我们使用属性范围来加速搜索过程,从而保持了硬实时能力,由于空间的限制,本文没有详细介绍k-最近搜索算法。感兴趣的读者可以参考开源库中的相关代码:https://github.com/hku-mars/ikd-Tree
应用实验
时间复杂性:ikd树的时间复杂性分为增量操作(插入、重新插入和删除)和重新构建的时间。
空间复杂度:增量kd树上的每个节点记录树的点信息、树大小、无效点数和点分布,对于逐框操作,在每个节点上都会维护额外的标志,例如惰性标签。对于具有n个节点的增量k-d树,虽然空间常数比静态k-d树大几倍,但其空间复杂度为O(n)。
A、 随机数据实验
通过对随机增量数据集的两个实验,全面研究了我们的ikd树的效率,第一个实验在10m×10m×10m的空间(即工作空间)中随机生成5000个点,以初始化增量k-d树。然后在k-d树上进行1000次测试操作。在每个测试操作中,将工作区中随机采样的200个新点(逐点)插入到kdtree中,然后在工作空间中随机抽取200个点,并在k-d树上搜索(但不插入)每个点中最近的5个点。对于每50次测试操作,在边长为1.5m的工作空间中对4个立方体进行采样,并从k-d树中删除(按框)这4个立方体中包含的点。对于每100次测试操作,在工作空间中采样2000个新点,并将其插入(逐点)到k-d树中。我们将ikd树与PCL中使用的静态k-d树进行比较,在每个测试操作中,k-d树都是完全重建的。这些实验是在一台装有Intel i7-10700 CPU、2.90GHz、仅运行2个线程的PC上进行的。表II总结了增量k-d树的参数,其中未使用下采样进行公平比较。

此外,允许存储在静态k-d树的叶节点上的最大点数设置为1,而PCL库中的原始设置为15。第一次实验的结果如图4所示,其中点数从5000增加到大约200000。在此过程中,ikd树上的增量更新(包括增量操作和重建)时间保持稳定在1.6 ms左右,而静态k-d树的增量更新时间随点数线性增长(见图4(a))。时间消耗的高峰是由大规模逐点插入(和相关的重新平衡)造成的,而低峰值是由框式删除(和相关的重新平衡)造成的。如图4(b)所示,ikd树上的k-最近搜索的时间性能略慢于静态k-d树,这可能是由于PCL库的高度优化实现。尽管查询效率略低,但ikd树的总体时间消耗比静态k-d树高一个数量级(见图4(c))。
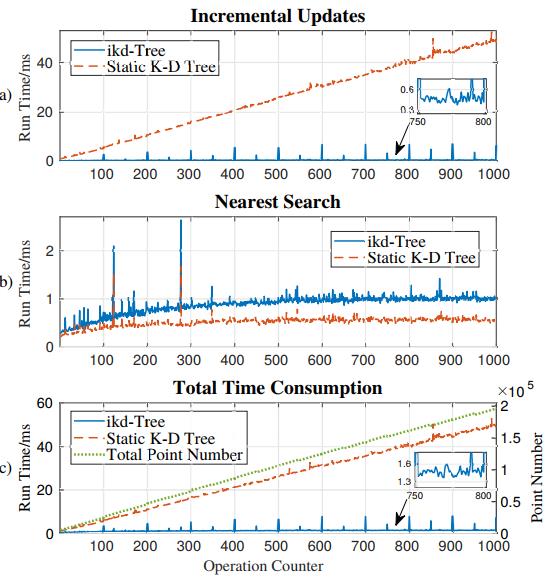
图4:ikd树与静态k-d树的时间性能比较
第二个实验研究了不同分布的新点的增量更新的时间性能,在实验中,我们在10m×10m×10m的空间(即工作空间)中采样了两组4000个新点:一组均匀分布(即稀疏数据,见图5(a)),另一组集中在2.5m×2.5m×2.5m的空间(即稠密数据,见图5(b))。将稀疏和稠密的数据插入到现有的不同大小的增量k-d树中,但所有数据都在工作空间中采样。图5(c)显示了不同大小的k-d树上稀疏和稠密的逐点插入的运行时间。正如预期的那样,稠密数据的增量更新比稀疏数据的增量更新慢,因为在将大量点插入k-d树的小子树时,更容易触发重建。
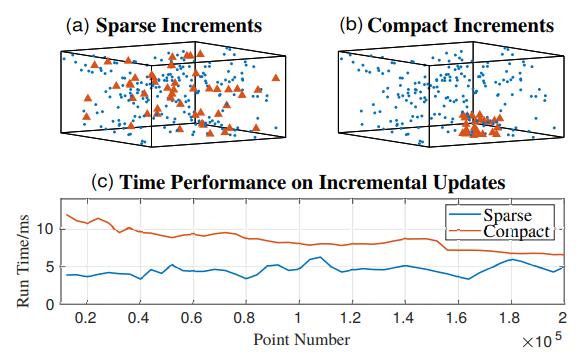
图5:图(a)和(b)显示了新点(橙色三角形)和k-d树上已有的点(蓝色点),图(c)显示了不同大小的k-d树上稀疏和紧凑数据的增量更新时间。
B、 激光雷达惯性里程计和建图
我们在实际的机器人应用中测试我们开发的ikd树:激光雷达惯性里程计(和建图图),在此应用中,基于k-d树的最近点搜索对于将新激光雷达扫描中的点与其在地图中的对应点(或之前的扫描)进行匹配至关重要,由于地图通过匹配和合并新扫描而动态增长,因此每次合并新扫描时都必须重新构建k-d树,现有方法通常使用PCL中的静态kd树,并基于地图(或子地图)中的所有点重建整个树,这导致了大量的计算成本,严重限制了map更新频率。
在本实验中,我们将静态k-d树(构建、更新和查询)替换为ikd树,它仅通过更新新点来实现地图的增量更新。我们在激光雷达惯性测绘包FAST LIO上测试了ikd树。该实验是在真实的室外场景中进行的,使用的是Livox Avia LiDAR3,视场为70°,帧速率高达100 Hz,在快速LIO中融合新激光雷达扫描的时间如图6(a)所示,时间是最近100次扫描的平均时间。可以看出,ikd树在1.6 ms左右实现了几乎恒定的时间性能,这从根本上实现了高达100Hz的建图速率(相对于原始作品中使用静态k-d树给出的10Hz)。另一方面,静态k-d树的时间总体呈线性增加,有时由于激光雷达当前FoV和地图之间的小重叠而减少,静态k-d树的最终处理时间从366s开始超过10 ms,这超过了一次激光雷达扫描的采集时间,融合新激光雷达扫描的时间包括许多操作,例如点配准、状态估计和kd树相关操作(包括查询和更新),kd树相关操作的时间分解如图6(b)所示,ikd树的平均增量更新时间为0.23 ms,仅为使用静态k-d树(5.71 ms)的4%。使用ikd树和静态k-d树进行最近搜索的平均时间是相同的。
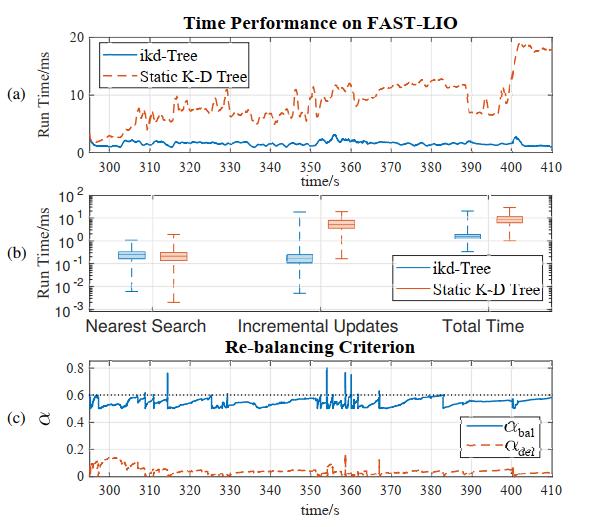
图6:图(a)显示了使用ikd树和静态k-d树在快速LIO中融合一个新激光雷达扫描的平均运行时间。图(b)显示了最近搜索、增量更新和融合一个激光雷达扫描的总时间。图(c)显示了在主线程中重建后的平衡特性。

图7:香港大学主楼的建图结果,绿线是由FAST LIO计算的携带激光雷达机器的路径
总结
本文提出了一种高效的数据结构ikd树,用于在机器人应用中增量更新k-d树,ikd树支持机器人的增量操作,同时通过部分重建保持平衡,我们提供了完整的时间和空间复杂性分析,以证明所提出的动态结构的高效性,ikd Tree通过随机实验和室外激光雷达里程计和地图实验进行测试,在所有测试中,所提出的数据结构实现了更高效率实现。
资源
三维点云论文及相关应用分享
【点云论文速读】基于激光雷达的里程计及3D点云地图中的定位方法
3D-MiniNet: 从点云中学习2D表示以实现快速有效的3D LIDAR语义分割(2020)
PCL中outofcore模块---基于核外八叉树的大规模点云的显示
更多文章可查看:点云学习历史文章大汇总
SLAM及AR相关分享
以上是关于ikd-Tree:增量KD树在机器人中的应用的主要内容,如果未能解决你的问题,请参考以下文章