SSD之硬的不能再硬的硬核解析
Posted 随煜而安
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SSD之硬的不能再硬的硬核解析相关的知识,希望对你有一定的参考价值。
本文是对经典论文 SSD: Single Shot MultiBox Detector 的解析,耗时3周完成,万字长文,可能是你能看到的最硬核的SSD教程了,如果想一遍搞懂SSD,那就耐心读下去吧~
一句话总结SSD效果就是:比YOLO快一点且准很多,比Faster R-CNN快很多且精度差不多(仅就当时时间线而言)。可见这篇paper在目标检测领域的重要性,话不多说,开始正文。
行文大致按照如下的流程进行:
- 首先尝试对SSD的设计思想进行解析,带你从大局观上把握SSD的精髓
- 随后尽可能全面的挖掘paper中的细节,并对照相应的pytorch版本SSD实现代码进行介绍
一、SSD设计思想解析
结合我自己的理解,在深入论文之前,这里先来解析下SSD的设计思想。
既然带检测目标物体的位置、大小、形状等情况多种多样,那么就暴力的预设大量的不同位置、不同尺度、不同长宽比的众多候选区域,来尽可能的cover住所有的情况。然后通过CNN端到端的一次性完成这些候选区域是否为关心的目标类别的预测,以及候选框与真实目标框之间偏差的预测,也就是对候选框进行微调,从而得到更好的目标框回归效果。

SSD的设计中有类似Faster R-CNN中anchor的概念,同时也能够看到YOLO的影子,可以说是对两者的优点都有借鉴。
下面我们来更为详细的解释这一设计理念:
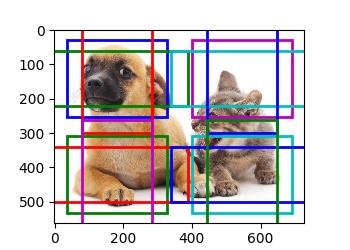
既然我们不知道待检测的图片中的物体大小,形状和位置,那么我们就尽可能罗列所有的情况。我们可能需要小一些的候选区域,那我们就按8*8,或者16*16的分辨率对原图进行初步的分割;同时我们我们也需要大一些的候选区域来检测大的物体,那我们也需要4*4、2*2、甚至1*1这样的分辨率。
我们可以这样认为,在初步划分候选区域大小后,每个划分出的小格子负责预测其相邻区域内出现的大小相当的物体。对于每个小格,我们可以再预设若干不同尺度以及长宽比之间的组合,来尽可能的涵盖所有可能遇到的情况。如下图我们可以看到,同一位置包含了长宽比1:1但尺度不同候选框,同时也包含了面积相同,但长宽比分别为1:1,2:1,1:2的候选框,从而能更好的囊括可能遇到的情况(下图仅为作者在paper中给出的示意图,实现细节可能会稍有差别)。

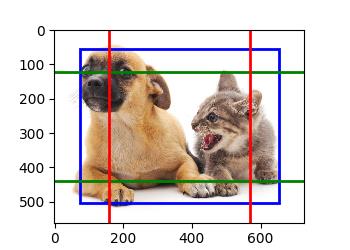
通过这样近乎暴力的候选区域的罗列,总有一些预选框在位置、大小、形状上大致的和图片中物体的真实情况向对应。例如蓝色和红色的虚线表示的预选框就分别很好的对应了图中的猫和狗。
现在我们要做的就是要让模型学会为每一个候选框预测以下两个信息:
- 候选框的类别(是背景,还是我们关心的目标类别,如猫、狗等)
- 目标物体的坐标(如果非背景,我们要学会预测候选框相对于真实目标框的坐标偏移量)
如何让模型学会为所有的候选框都完成这样的预测呢?最直接的想法,我们当然可以像R-CNN的做法一样为每个候选区域应用一个CNN来完成类别和坐标的预测。

这样做的一个致命问题就是速度实在堪忧,因为候选框实在太多。Ross Girshick大神已经在R-CNN -> Fast R-CNN -> Faster R-CNN 的发展历程中给了我们的答案:
我们用来预测目标类别和坐标的输入不必是原始图像的rgb信息,也可以是CNN提取的更为抽象的高层特征,通过感受野的概念完成原始图像中某块感兴趣区域与特征层feature map中相应区域的对应。这样我们就可以通过一次前向推理,得到所有的候选区域对应的特征,在此基础上完成类别和坐标预测,进而大幅提高速度。
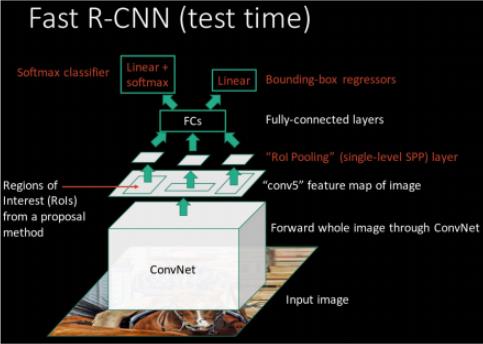
YOLO也是利用卷积层提取的信息作为特征来进行最后的类别和坐标预测。
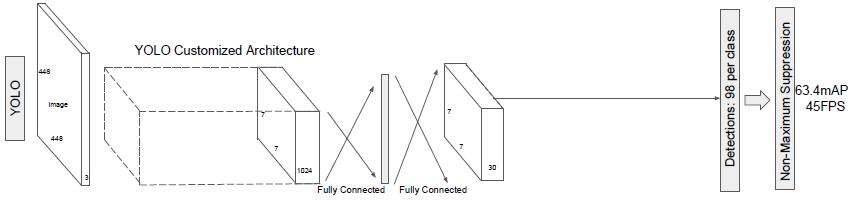
可以看到,这种思路已经成为了公认的设计思路。需要注意的是,无论是Fast R-CNN、Faster R-CNN还是YOLO,为每个候选区域提取的特征都来自同一高层特征layer对应的feature map。
而SSD的主要贡献就是来源对于这个机制的改变,完全可以将不同的特征层的feature map利用起来。既然我们想设置不同尺度的预选框,那么我们就可以利用不同特征层感受野不同的这个特点,将小尺度的候选框分配给比较靠近输入层的感受野小的浅层特征层来预测,将大尺度的候选框分配给远离输入层的感受野大的高层特征层来预测。

这样就做到了一次推理完成了多种尺度预选框的预测,即SSD名字The Single Shot Detector (单发多框检测器)的由来。我认为这也就是SSD的精髓所在,端到端的一阶段方法保证了速度,多尺度的大量预选框保证了召回和map指标。
作者在 第一章 Introduction 中将SSD贡献总结如下:
- 提出了SSD,一句话总结其效果就是:比YOLO快一点且准很多,比Faster R-CNN快很多且精度差不多
- SSD的核心是使用应用于特征图上的小的卷积滤波器来预测一组预先设置好的默认bounding box的类别分数和位置坐标的偏移。
- 为了获得高准确率,我们在不同分辨率的特征图上进行预测,并且使用不同大小和长宽比的默认bbox。
- 这样的设计带来了简单的端到端训练和高准确率,即使在低分辨率的输入图像上,这进一步提升了速度和准确性的平衡问题。
到这里我们已经对SSD的设计初衷以及前向推理框架有了大致的了解,下面进入到paper中来仔细探索。
paper的内容安排:2.1小节介绍SSD框架,2.2介绍训练方法,第三者介绍数据集相关的模型细节和实验结果。
二、模型结构
SSD网络的靠前的部分基于分类问题的标准网络架构(在分类layer之前进行截断),后面我们将其叫做 base network(基础网络)。本文使用VGG-16作为基础网络,其它优秀的backbone也是可以的。
在基础网络的基础上我们加上一些辅助结构,以产生具有以下特性的检测结果:
- Multi-scale feature maps for detection 多尺度的特征图
- Convolutional predictors for detection 使用卷积进行检测
- Default boxes and aspect ratios 设置默认检测框与宽高比(类似于Faster R-CNN种anchor的设置)
其实前面关于SSD设计思想的讨论中已经设计了这些概念,下面我们再对其中的一些细节进行讲解。
多尺度的特征图
在截断的base network上添加若干卷积层,使得特征图尺寸逐渐平滑的下降到1*1,从而最终得到多个尺度下的检测框预测。每个尺度的特征层都使用独立的卷积层进行预测。(Overfeat和YOLO都只在一个单一尺度的特征图上进行预测)
SSD原版的实现输入shape固定为300*300,使用了6个不同的尺度,分别是利用了Conv4_3、Conv7、Conv8_2、Conv9_2、Conv10_2和Conv11_ 2 这些层的feature maps作为检测框预测的输入特征。
其中,Conv4_3,Conv7来自VGG的base network:

其中conv7较为特殊,为了后面继续接卷积层,作者将原版vgg中的全连接fc6,fc7替换为了卷积层conv6和conv7,同时还起到了加速的作用。
这部分比较trick,也有点炫技的成分~ 作者的原版描述如下,感兴趣可以跟进下,这里就不展开了。
Similar to DeepLab-LargeFOV [17], we convert fc6 and fc7 to convolutional layers, subsample parameters from fc6 and fc7, change pool5 from 2 × 2 - s2 to 3 × 3 - s1, and use the `a trous algorithm [18] to fill the ”holes”.
[18] Holschneider, M., Kronland-Martinet, R., Morlet, J., Tchamitchian, P.: A real-time algorithm for signal analysis with the help of the wavelet transform. In: Wavelets. Springer (1990) 286–297
vgg基础网络部分的pytorch代码实现如下:
# This function is derived from torchvision VGG make_layers()
# https://github.com/pytorch/vision/blob/master/torchvision/models/vgg.py
def vgg(cfg, i, batch_norm=False):
""" 构造vgg backbone
cfg: (list), 表示模型参数的列表,示例:[64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'C', 512, 512, 512, 'M', 512, 512, 512]
i: (int), 输入channel个数
"""
layers = []
in_channels = i
for v in cfg:
if v == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
elif v == 'C':
layers += [nn.MaxPool2d(kernel_size=2, stride=2, ceil_mode=True)] # ceil_mode 向上取整
else:
conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
if batch_norm:
layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
else:
layers += [conv2d, nn.ReLU(inplace=True)]
in_channels = v
pool5 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
conv6 = nn.Conv2d(512, 1024, kernel_size=3, padding=6, dilation=6)
conv7 = nn.Conv2d(1024, 1024, kernel_size=1)
# 在vgg16 basenet基础上补的pool5,conv6,conv7这三个层用来替代vgg16原本的全连接层
# conv6的设置很有意思,参考paper参考文献[18]
# dilation参数的作用可以见https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
layers += [pool5, conv6,
nn.ReLU(inplace=True), conv7, nn.ReLU(inplace=True)]
return layers
Conv8_2、Conv9_2、Conv10_2和Conv11_ 2 这4层来自在基础网络上额外添加的卷积层。 其代码实现如下:
def add_extras(cfg, i, batch_norm=False):
"""
Extra layers added to VGG for feature scaling
cfg: 配置信息,示例: [256, 'S', 512, 128, 'S', 256, 128, 256, 128, 256],
i: 输入channel维度
注:这个函数共包含了4次下采样,这点容易产生困惑
由vgg16的base模块输入的特征图shape为19,四次下采样的变化分别为19->10->5->3->1,注意观察本函数的实现细节。
四次特征图发生变化的位置: [256, 'S', 512, 128, 'S', 256, 128, 256, 128, 256],
↑ ↑ ↑ ↑
19->10 10->5 5->3 3->1
"""
layers = []
in_channels = i
flag = False
for k, v in enumerate(cfg):
if in_channels != 'S':
if v == 'S':
layers += [nn.Conv2d(in_channels, cfg[k + 1],
kernel_size=(1, 3)[flag], stride=2, padding=1)]
else:
layers += [nn.Conv2d(in_channels, v, kernel_size=(1, 3)[flag])] # 注意这里的Conv2d没有padd,因此shape会发送变化
flag = not flag
in_channels = v
return layers
通过上面的介绍和给出的代码,不难自行验证出 Conv4_3、Conv7、Conv8_2、Conv9_2、Conv10_2 和 Conv11_ 2 这6层卷积层的feature maps的shape分别为,38->19->10->5->3->1。
使用卷积进行检测
对于每个用于检测的特征层,通过卷积来进行每个位置对应的预设bbox的类别预测和坐标offset的预测。(R-CNN中使用SVM来进行分类的预测,YOLO使用全连接层作为过渡来完成预测)
这部分对应的代码实现:
192 def multibox(vgg, extra_layers, cfg, num_classes):
193 """
194 cfg: [4, 6, 6, 6, 4, 4], # number of boxes per feature map location
195 """
196 loc_layers = []
197 conf_layers = []
198 vgg_source = [21, -2]
199 for k, v in enumerate(vgg_source):
200 loc_layers += [nn.Conv2d(vgg[v].out_channels,
201 cfg[k] * 4, kernel_size=3, padding=1)]
202 conf_layers += [nn.Conv2d(vgg[v].out_channels,
203 cfg[k] * num_classes, kernel_size=3, padding=1)]
204 for k, v in enumerate(extra_layers[1::2], 2):
205 loc_layers += [nn.Conv2d(v.out_channels, cfg[k]
206 * 4, kernel_size=3, padding=1)]
207 conf_layers += [nn.Conv2d(v.out_channels, cfg[k]
208 * num_classes, kernel_size=3, padding=1)]
209 return vgg, extra_layers, (loc_layers, conf_layers)
完整的网络结构代码见ssd.py,篇幅原因这里就不放了。
默认检测框与宽高比
我们将特征图的每个单元通过位置与若干预设的不同尺寸和长宽比的默认检测框对应起来。对于特征图的每一个单元,我们需要为其对应的不同尺寸和长宽比的默认检测框预测其属于每一个类别的概率以及位置相对于ground truth的偏移量。特别地,假设一个单元对应了k个默认检测框,每一个检测框我们需要预测c个类别分数以及4个位置偏移量,因此一个m*n的特征图将会产生形状为m*n*[(c+4)*k]的输出。默认检测框的设置类似Faster R-CNN中anchor boxes的设置,相比paper中作者给出的描述图,下面的示意图更符合代码实现。

我们为每一个尺度下的候选框,都定义一个 min_size 和 一个 max_size,且某一尺度下候选框的 max_size 是其更大一级尺度的 min_size。
以长宽比1:1,大小为min_size的候选框为基准(如上图较小的红色框),又应用了与其面积相同,但长宽比不同的候选框(如上图绿色框所示)。此外,单独应用了一个尺寸为
m
i
n
s
i
z
e
∗
m
a
x
s
i
z
e
\\sqrtminsize * maxsize
minsize∗maxsize,长宽比1:1的候选框(如上图较大红色框所示)。
作者在2.2 training 中的 Choosing scales and aspect ratios for default boxes 一段,对 min_size 和 max_size 的设置又做了进一步的阐述。

正如上文所述,作者使用了平铺的策略来让多尺度策略均匀的涵盖所有的目标物体的大小。所谓平铺就是在设置的左右区间范围内,让尺度均匀地分布。这里的s_min = 0.2 指的是相对于原图尺寸的比例,其余的信息公式表达的已经很清楚了。
为什么可以这样设置呢?我们知道一个网络中来自不同层的特征图具有其特定的感受野,随着网络的加深感受野越来越大。使用了平铺的策略正好可以利用这一点来为不同的特征层分配了不同的默认目标框尺寸,浅层特征层分配的尺度小,深层特征分配的尺度大,这样分配的尺度就和其理论的感受野大致相符。
关于这块的详细设置,可以在 data/config.py文件中找到
# SSD300 CONFIGS
voc =
'num_classes': 21,
'lr_steps': (80000, 100000, 120000),
'max_iter': 120000,
'feature_maps': [38, 19, 10, 5, 3, 1],
'min_dim': 300,
'steps': [8, 16, 32, 64, 100, 300],
'min_sizes': [30, 60, 111, 162, 213, 264],
'max_sizes': [60, 111, 162, 213, 264, 315],
'aspect_ratios': [[2], [2, 3], [2, 3], [2, 3], [2], [2]], # 宽高比,只需设置宽高比大于1的情况,相反的情况将会自动处理
'variance': [0.1, 0.2],
'clip': True, # 设置是否裁剪anchor越界的情况
'name': 'VOC',
代码中的设置和paper中还是有点小区别的,SSD共有6个不同的尺度前面已经说过了,实现中第一个最小的尺度是单独设置的,后面5个尺度是按照paper所述的方法进行的平铺,如下表,我们自己算一下就和代码对应上了。
| min_size 比例值 | 0.1 | 0.2 | 0.375 | 0.55 | 0.725 | 0.9 |
|---|---|---|---|---|---|---|
| min_size 绝对值 | 30 | 60 | 111 | 162 | 213 | 264 |
| max_size 绝对值 | 60 | 111 | 162 | 213 | 264 | 315 |
关于不同的长宽比,从代码就可以看到,应该是考虑到大小适中的目标框出现的概率更多,作者为中间的几种尺度额外设置了1:3和3:1长宽比的默认框。
此外,代码中的steps 其实就是对应尺度下每一个小格的步长,例如第一个尺度为38*38,那么 steps[0] = 300 / 38 ≈ 7.89 向上取整 = 8
这一步涉及了蛮多细节,也有蛮多可调整的参数,我们不用纠结这些参数的取值,而是需要思考作者这些设计背后的用意,从而在我们的实际问题中灵活调整。作者自己也在paper中表述了,如何更好的设置这些候选框或者说anchor,本身就是一个开放问题,后续工作也会继续研究。
我们已经扣了所有关于候选框生成的细节,下面再对照着代码巩固下。在 layers/functions/prior_box.py 中可以找到候选框生成部分的代码:
class PriorBox(object):
"""Compute priorbox coordinates in center-offset form for each source
feature map.
"""
def __init__(self, cfg):
super(PriorBox, self).__init__()
self.image_size = cfg['min_dim']
# number of priors for feature map location (either 4 or 6)
self.num_priors = len(cfg['aspect_ratios'])
self.variance = cfg['variance'] or [0.1]
self.feature_maps = cfg['feature_maps']
self.min_sizes = cfg['min_sizes']
self.max_sizes = cfg['max_sizes']
self.steps = cfg['steps']
self.aspect_ratios = cfg['aspect_ratios']
self.clip = cfg['clip']
self.version = cfg['name']
for v in self.variance:
if v <= 0:
raise ValueError('Variances must be greater than 0')
def forward(self):
mean = []
for k, f in enumerate(self.feature_maps):
for i, j in product(range(f), repeat=2):
f_k = self.image_size / self.steps[k]
# unit center x,y
cx = (j + 0.5) / f_k
cy = (i + 0.5) / f_k
# aspect_ratio: 1
# rel size: min_size
s_k = self.min_sizes[k]/self.image_size
mean += [cx, cy, s_k, s_k]
# aspect_ratio: 1
# rel size: sqrt(s_k * s_(k+1))
s_k_prime = sqrt(s_k * (self.max_sizes[k]/self.image_size))
mean += [cx, cy, s_k_prime, s_k_prime]
# rest of aspect ratios
for ar in self.aspect_ratios[k]:
mean += [cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]
mean += [cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]
# back to torch land
output = torch.Tensor(mean).view(-1, 4)
if self.clip:
output.clamp_(max=1, min=0)
return output
三、训练
回忆一下,我们已经介绍了SSD的模型结构,多尺度默认候选框的选择和设置,前向推理的过程以及输出所代表的含义。
下面我们介绍如何训练SSD来让模型正确的学会我们所期望其学会的信息:即每个候选框的类别以及相对于真实目标框ground truth的坐标偏移。达到这一目标的关键是需要将 ground truth 信息分配给网络输出的默认候选检测框。一旦确定了这个分配,就可以端到端地应用损失函数和反向传播。
paper作者在训练过程种还使用了负样本难例挖掘(hard negtive mining)和数据扩充策略(data augmentation strategies),我们也会分别介绍。
匹配策略
训练过程中我们需要决定哪些默认的候选目标框是和真实的目标框是有匹配关系的,从而标注出每个候选目标框的期望预测结果,进而应用损失函数进行训练。
正如下图所示,我们很可能会认为,两个蓝色虚线框代表的候选目标框和猫的蓝色真实目标框是匹配的,红色虚线框代表的候选目标框和狗狗对应的红色真实目标框是匹配的,而其余的黑色虚线候选框和任何真实目标都是不匹配的,无论是猫和狗。一旦建立了这样的映射,我们就可以很方便的对模型的预测应用损失函数,对错误的预测进行惩罚,从而学习到正确的信息。

我们的大脑似乎很自然的就完成了这个匹配过程,那么我们如何将这个过程归纳成一个有固定模式的匹配策略呢?
首先我们要定义如何衡量单独的一对目标框之间的匹配程度,像大多数方法一样,SSD通过 jaccard overlap(对于矩形框来说就是IOU) 来衡量默认目标框和真实目标框之间的匹配程度。
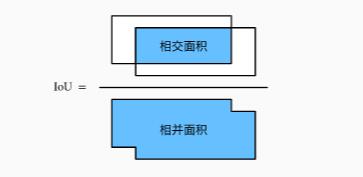
然后我们需要计算所有真实目标框与所有候选框之间的overlap矩阵。矩阵的函数为真实目标框的个数,列数为候选框的个数,第i行第j列的元素是第i个真实目标框和第j个候选框之间的IOU。
大体上,我们找到每一列的最大值,就相当于为每一个预设候选框找到了最匹配的真实框,然后通过一个IOU阈值来判断这是否是一个满足要求的匹配。在此基础上,paper作者加入了一个强制匹配机制,来确保每个真实框都能够有预设的候选框与其匹配。这里我们不讨论这样的匹配机制的好与坏,而是先试图把这个匹配策略的每一个环节解释清楚。
我们拿个示例来说明可能会更加清晰,假设我们有3个真实的ground truth目标框,5个prior boxes候选框,计算得到了如下的overlap矩阵。
| priorA | priorB | priorC | priorD | priorE | |
|---|---|---|---|---|---|
| gtA | 0.8 | 0.1 | 0 | 0 | 0 |
| gtB | 0 | 0.5 | 0.7 | 0.9 | 0.1 |
| gtC | 0 | 0.2 | 0.1 | 0 | 0 |
匹配策略分为两步:
第一步是先将每一个真实框和与其具有最高 jaccard overlap 的默认框进行强制匹配,这样的操作确保了无论后面的操作如何进行,每一个真实框都至少与一个候选框完成了匹配。
代码中通过将IOU匹配度强制赋值2来实现(因为IOU最大为1,强制也就体现在了这里),于是overlap矩阵变为:
| priorA | priorB | priorC | priorD | priorE | |
|---|---|---|---|---|---|
| gtA | 2 | 0.1 | 0 | 0 | 0 |
| gtB | 0 | 0.5 | 0.7 | 2 | 0.1 |
| gtC | 0 | 2 | 0.1 | 0 | 0 |
可以看到,priorB被强制匹配给了gtC,尽管预选框priorB似乎和gtB更加匹配,因为实在是没有其它预选框和gtC匹配了。我想这个例子已经很好的解释了作者的这个强制匹配策略。
然后第二步是将剩余的默认框和与其具有最高 jaccard overlap 的真实框进行匹配(前提是IOU大于阈值0.5),相当于进行按列求最大值。于是得到匹配结果:
| priorA | priorB | priorC | priorD | priorE | |
|---|---|---|---|---|---|
| 匹配类别 | gtA | gtC | gtB | gtB | background |
可以看到,SSD的匹配策略是允许多个候选框和同一个真实目标框进行匹配的,且同一个真实目标框至少匹配了一个候选框。
匹配过程实现的细节见layers/box_utils.py 中的 match 函数
目标函数
SSD的目标函数总体形式是分类损失和坐标回归损失的加权和。
L ( x , c , l , g ) = 1 N ( L c o n f ( x , c ) + α L l o c ( x , l , g ) ) L(x, c, l, g)=\\frac1N\\left(L_c o n f(x, c)+\\alpha L_l o c(x, l, g)\\right) L(x,c,l,g)=N1(Lconf(x,c以上是关于SSD之硬的不能再硬的硬核解析的主要内容,如果未能解决你的问题,请参考以下文章