IIR数字滤波器的设计

Posted

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了IIR数字滤波器的设计相关的知识，希望对你有一定的参考价值。

参考技术A

利用MATLAB信号处理工具箱中的滤波器设计和分析工具(FDATool)可以很方便地设计出符合应用要求的未经量化的IIR数字滤波器。需要将MATLAB设计出的IIR数字滤波器进一步分解和量化，从而获得可用FPGA实现的滤波器系数。
IIR数字滤波器的设计方法有两类：间接设计法和直接设计法。间接设计法是借助模拟滤波器设计方法进行设计的，先根据数字滤波器设计指标设计相应的过渡模拟滤波器，再将过渡模拟滤波器转换为数字滤波器。直接设计法师在时域或频域直接设计数字滤波器。
由于模拟滤波器设计理论非常成熟，而且有很多性能优良的典型滤波器可供选择（如，巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等），设计公式和图表完善，而且许多实际应用需要模拟滤波器的数字仿真，所以间接设计法得到广泛的应用。而直接设计法要求解联立方程组，必须采用计算机辅助设计。在计算机普及的今天，各种设计方法都有现成的设计程序（或设计函数）可供调用，例如利用MATLAB仿真平台，可以设计不同类型的IIR滤波器。 3.1.1性能指标确定
按照实际需要确定滤波器的性能要求，比如确定所要设计的滤波器是低通、高通、带通还是带阻，截止频率是多少，阻带的衰减有多大，通带的波动范围是多少等等。
3.1.2系统函数确定
用一个因果稳定的系统函数(或差分方程、脉冲响应h(n))去逼近上述性能要求。此系统函数可分为两类，即IIR系统函数与FIR系统函数。
3.1.3算法设计
用一个有限精度的运算去实现这个系统函数（速度、开销、稳定性等)。这里包括选择算法结构，如级联型、并联型、正准型、横截型或频率采样型等等；还包括选择合适的字长以及选择有效的数字处理方法等。
3.2 IIR数字滤波器的直接设计法
直接设计可以采用优化设计（CAD）法，数字滤波器的系统函数H（Z）的系数ai, bi或零极点ci, di等参数，可采用优化设计的方法。设计步骤：
1. 优化原则——最小均方误差准则，绝对误差准则等。
2. 赋予初值.
3. 一次次的改变参数赋值，根据优化准则计算误差。
4. 改变参数赋值，再次计算误差，如此迭代下去，直至误差达到最小。示意图如下
间接设计法的设计过程如下：
1） 确定数字滤波器指标；
2） 将数字滤波器指标转换为相应的模拟滤波器指标；
3） 设计满足指标要求的过渡模拟函数(s)；
4） 将过渡模拟函数(s)转换为数字滤波器H(z)。示意图如下：

把模拟滤波器Ha(S) 转换为数字滤波器H(z)的实质是，用一种从s平面到z平面的映射函数将Ha(S) 转换H(z)。对这种映射函数的要求是：因果稳定的模拟滤波器转换为数字滤波器H(z)后仍然稳定；数字滤波器H(z)的频率响应特性能够近似模仿数字滤波器Ha(S)的片段常数频率响应特性。常用的模拟-数字滤波器变换方法有：脉冲响应不变法和双线性变换法，也就是根据两种准则。
3.3.1 脉冲响应不变法
步骤：
1）对已知的(s) 进行拉氏反变换，求得(t)；(t) (nt)
2）对(t) 进行取样，得(nt)；
3）令h(n)=T(nt)，以求得h(n)；
4）对h(n) 进行Z 变换，得H（Z）。
3.3.2双线性变换
由于脉冲响应不变法存在缺点，即因为z=映射关系不是单值对应，所以，从s 平
面直接映射到z 平面时会产生混迭现象，而且脉冲响应不变法只适合频率响应在高频处单调递减的模拟原型滤波器，因此其应用范围受到限制。
双线性变换法的主要目的是从根本上解决上述脉冲响应不变法的问题也付出了一定的代价。
双线性变换法基本步骤：
1) 构造从S 平面到S1 平面的单值映射 :Ω = A tan(T/2)
2) 构造从S1 平面到Z 平面的单值映射： ω = T
实际上，不需要每次都从S 平面→S1平面→Z平面，而是直接求出S=f(Z) 的关系，然后代入Ha(s)，得H(z)，即H(z) = Ha(s)|s = f(z)。

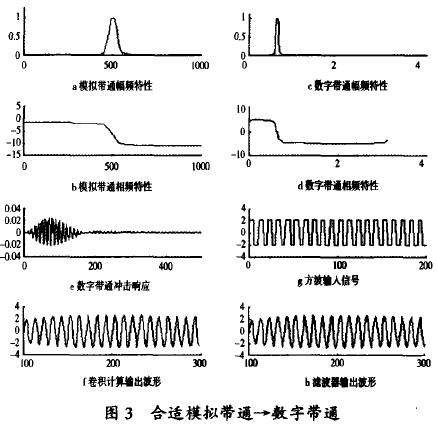
实验六 基于MATLAB的IIR数字滤波器设计

目录

一、实验目的：

1．加深对IIR数字滤波器常用指标的理解；
2．学会设计IIR数字滤波器；
3．根据指标要求设计数字滤波器，并进行信号的处理。

二、实验原理：

1.脉冲响应不变法

MATLAB提供impinvar(num,den,Fs)函数，可以实现利用脉冲响应不变法将模拟滤波器转换为数字滤波器，其调用形式为：
[numd,dend]=impinvar(num,den,Fs)
式中num和den分别表示模拟滤波器系统函数H（s）的分子多项式系统和分母多项式系数，Fs是脉冲响应不变法中的抽样频率，单位是Hz。输出变量numd和dend分别表示数字滤波器系统函数H（z）的分子多项式系统和分母多项式系数。
【例6.1】利用BW型低通滤波器及脉冲响应不变法设计满足下列指标的数字滤波器。
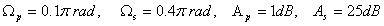
在这里插入图片描述

程序如下：

     clear all 	
         Wp=0.1*pi;
         Ws=0.4*pi;
         Ap=1;
         As=25;
         T=1;
         Fs=1/T;
         wp=Wp*Fs;
         ws=Ws*Fs;
         N=buttord(wp,ws,Ap,As,'s');
         wc=wp/(10^(0.1*Ap)-1)^(1/2/N);
         [num den]=butter(N,wc,'s');
         [numd,dend]=impinvar(num,den,Fs);
         w=linspace(0,pi,512);
        h=freqz(numd,dend,w);
        plot(w/pi,abs(h));
		title('脉冲响应不变法');
        %计算所设计滤波器的Ap和As
        w1=[Wp,Ws];
        h1=freqz(numd,dend,w1);
        fprintf('Ap= %.4f\\n',-20*log10(abs(h1(1))));
        fprintf('As= %.4f\\n',-20*log10(abs(h1(2))));

运行结果：
Ap= 0.9991
As= 30.3245
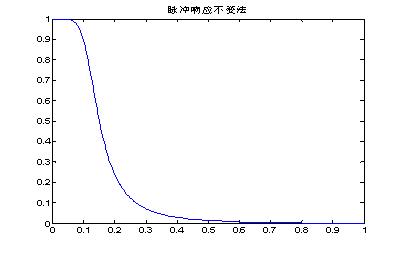
在这里插入图片描述

          图1 数字低通滤波器的幅度响应

2.双线性变换法

MATLAB提供bilinear(num,den,Fs)函数，可以实现利用双线性变换法将模拟滤波器转换为数字滤波器，其调用形式为：
[numd,dend]=bilinear(num,den,Fs)
式中num和den分别表示模拟滤波器系统函数H（s）的分子多项式系统和分母多项式系数，Fs=1/T。输出变量numd和dend分别表示数字滤波器系统函数H（z）的分子多项式系统和分母多项式系数。
【例6.2】利用CB1型滤波器及双线性变换法设计满足下列指标的数字高通滤波器。
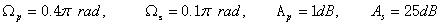
在这里插入图片描述

程序如下：

		clear all   
         Wp=0.4*pi;
         Ws=0.1*pi;
         Ap=1;
         As=25;
         T=2;
         Fs=1/T;
         wp=(2/T)*tan(Wp/2);
         ws=(2/T)*tan(Ws/2);
         [N,wc]=cheb1ord(wp,ws,Ap,As,'s');
         [num den]=cheby1(N,Ap,wc,'high','s');     
    	 [numd,dend]=bilinear(num,den,Fs);
         w=linspace(0,pi,512);
         h=freqz(numd,dend,w);
         plot(w/pi,abs(h));
            title('双线性变换法')
         %计算所设计滤波器的Ap和As       
		 w1=[Wp,Ws];
        h1=freqz(numd,dend,w1);
        fprintf('Ap= %.4f\\n',-20*log10(abs(h1(1))));
        fprintf('As= %.4f\\n',-20*log10(abs(h1(2))));

运行结果：
Ap= 1.0000
As= 26.4153
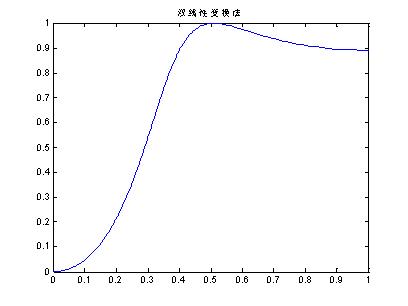
在这里插入图片描述

			图2 数字高通滤波器的幅度响应

3.数字滤波函数

（1）filter函数用来实现数字滤波器对数据的滤波，函数调用格式为：
y=filter(numd,dend,x)
其中，numd和dend分别为滤波器系统函数H（z）的分子和分母多项式的系数，x为滤波器的输入，y为滤波器的输出，y与x具有相同大小的向量。
（2）filtfilt函数实现零相位前后与后向结合滤波，其调用格式为：
y=filtfilt(numd,dend,x)
其中，numd和dend分别为滤波器系统函数H（z）的分子和分母多项式的系数，x为滤波器的输入，y为滤波器的输出，y与x具有相同大小的向量，这个函数实现的滤波后其输出信号与输入信号的相位一致，也就是没有改变信号波形形状。但filter函数滤波后有一些延迟，改变了信号的形状。

三、作业：

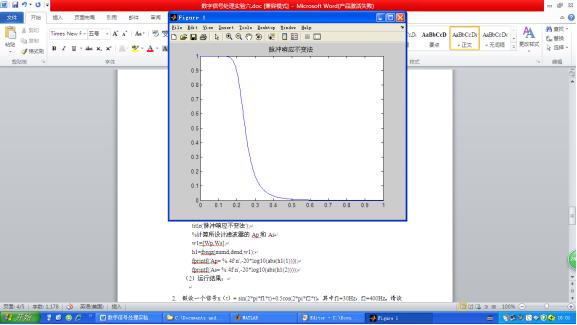
1.设计Butterworth低通数字滤波器，要求通带截止频率为0.2pi(rad) ,通带波纹小于1dB，阻带截频为0.3pi（rad），幅度衰减大于15dB，采样周期为0.01s。画出滤波器的幅频图像。
(1)示例代码：

clear all 	
Wp=0.2*pi;
Ws=0.3*pi;
Ap=1;
As=15;
T=0.01;
Fs=1/T;
wp=Wp*Fs;
ws=Ws*Fs;
N=buttord(wp,ws,Ap,As,'s');
wc=wp/(10^(0.1*Ap)-1)^(1/2/N);
[num den]=butter(N,wc,'s');
[numd,dend]=impinvar(num,den,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
plot(w/pi,abs(h));
title('脉冲响应不变法');
%计算所设计滤波器的Ap和As
w1=[Wp,Ws];
h1=freqz(numd,dend,w1);
fprintf('Ap= %.4f\\n',-20*log10(abs(h1(1))));
fprintf('As= %.4f\\n',-20*log10(abs(h1(2))));

（2）运行结果：

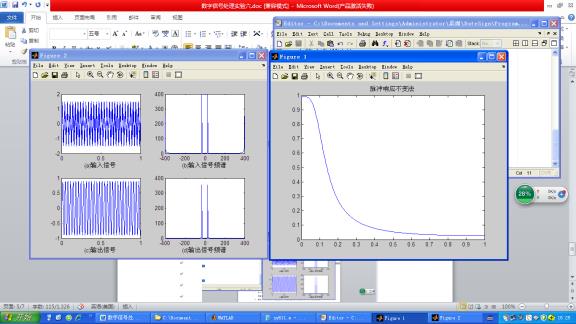
在这里插入图片描述

2.假设一个信号x（t）= sin(2pif1t)+0.5cos(2pif2t)，其中f1=30Hz，f2=400Hz。请设计一个IIR数字滤波器，将f2滤除掉。请写出程序，并画出原信号与原信号通过滤波器的输出信号的图形。（数字低通滤波器）
（1）示例代码：

clear all 	
Wp=0.075*pi;
Ws=1*pi;
Ap=1;
As=25;
T=0.01;
Fs=1/T;
wp=Wp*Fs;
ws=Ws*Fs;
N=buttord(wp,ws,Ap,As,'s');
wc=wp/(10^(0.1*Ap)-1)^(1/2/N);
[num den]=butter(N,wc,'s');
[numd,dend]=impinvar(num,den,Fs);


w=linspace(0,pi,512);
h=freqz(numd,dend,w);
plot(w/pi,abs(h));
title('脉冲响应不变法');
%计算所设计滤波器的Ap和As
w1=[Wp,Ws];
h1=freqz(numd,dend,w1);
fprintf('Ap= %.4f\\n',-20*log10(abs(h1(1))));
fprintf('As= %.4f\\n',-20*log10(abs(h1(2))));
%信号传输
fs=800;
dt=1/fs;   %模拟信号采样间隔
f1=30;f2=400;
t=0:dt:1;
x=sin(2*pi*f1*t)+0.5*cos(2*pi*f2*t);
y=filter(numd,dend,x); % 模拟输出
L=length(x);
x1=fftshift(fft(x));
ff=(-L/2:L/2-1)*fs/L;
y1=fftshift(fft(y));
figure(2)
subplot(2,2,1)
plot(t,x);
xlabel ('(a)输入信号');
subplot(2,2,2)
plot(ff,abs(x1));
xlabel ('(b)输入信号频谱');
subplot(2,2,3)
plot(t,y);
xlabel('(c)输出信号');
subplot(2,2,4)
plot(ff,abs(y1));
xlabel ('(d)输出信号频谱'

（2）运行结果：

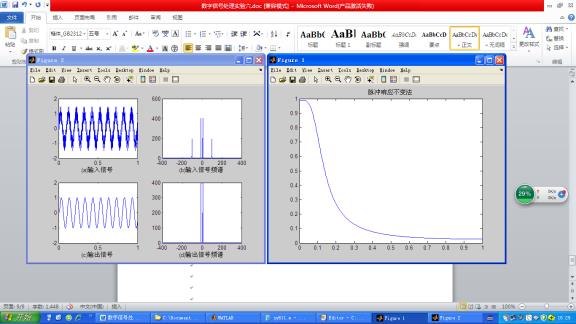
在这里插入图片描述

3.假设一个信号x（t）= sin(2pif1t)+0.5cos(2pif2t)，其中f1=10Hz，f2=100Hz。请设计一个IIR数字滤波器能把f1滤除掉，请写出程序，并画出原信号与原信号通过滤波器的输出信号的图形。
（1）示例代码：

clear all 	
Wp=0.1*pi;
Ws=0.2*pi;
Ap=1;
As=25;
T=1;
Fs=1/T;
wp=(2/T)*tan(Wp/2);
ws=(2/T)*tan(Ws/2);
[N,wc]=cheb1ord(wp,ws,Ap,As,'s');
[num den]=butter(N,wc,'s');
[numd,dend]=impinvar(num,den,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
plot(w/pi,abs(h));
title('脉冲响应不变法');
%计算所设计滤波器的Ap和As
w1=[Wp,Ws];
h1=freqz(numd,dend,w1);
fprintf('Ap= %.4f\\n',-20*log10(abs(h1(1))));
fprintf('As= %.4f\\n',-20*log10(abs(h1(2))));
%信号传输
fs=800;
dt=1/fs;   %模拟信号采样间隔
f1=10;f2=100;
t=0:dt:1;
x=sin(2*pi*f1*t)+0.5*cos(2*pi*f2*t);
y=filter(numd,dend,x); % 模拟输出
L=length(x);
x1=fftshift(fft(x));
ff=(-L/2:L/2-1)*fs/L;
y1=fftshift(fft(y));
figure(2)
subplot(2,2,1)
plot(t,x);
xlabel ('(a)输入信号');
subplot(2,2,2)
plot(ff,abs(x1));
xlabel ('(b)输入信号频谱');
subplot(2,2,3)
plot(t,y);
xlabel('(c)输出信号');
subplot(2,2,4)
plot(ff,abs(y1));
xlabel ('(d)输出信号频谱');

（2）运行结果：

在这里插入图片描述

4.假设一个信号x（t）=sin(2pif1t)+sin(2pif2t)+sin(2pif3*t),其中f1=200Hz，f2=1500Hz，f3=2900Hz。请设计一个IIR数字滤波器能把f2保留，请写出程序，并画出原信号与原信号通过滤波器的输出信号的图形。
（1）示例代码：

clear all 	
Wp=[0.2*pi 0.4*pi];
Ws=[0.1*pi 0.5*pi];
Ap=1;
As=25;
T=1;
Fs=1/T;
wp=(2/T)*tan(Wp/2);
ws=(2/T)*tan(Ws/2);
[N,wc]=cheb1ord(wp,ws,Ap,As,'s');
wc=wp/(10^(0.1*Ap)-1)^(1/2/N);
[num den]=butter(N,wc,'s');
[numd,dend]=impinvar(num,den,Fs);
w=linspace(0,pi,512);
h=freqz(numd,dend,w);
plot(w/pi,abs(h));
title('脉冲响应不变法');
%计算所设计滤波器的Ap和As
w1=[Wp,Ws];
h1=freqz(numd,dend,w1);
fprintf('Ap= %.4f\\n',-20*log10(abs(h1(1))));
fprintf('As= %.4f\\n',-20*log10(abs(h1(2))));
%信号传输
fs=800;
dt=1/fs;   %模拟信号采样间隔
f1=200;f2=1500;f3 = 2900;
t=0:dt:1;
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t);
y=filter(numd,dend,x); % 模拟输出
L=length(x);
x1=fftshift(fft(x));
ff=(-L/2:L/2-1)*fs/L;
y1=fftshift(fft(y));
figure(2)
subplot(2,2,1)
plot(t,x);
xlabel ('(a)输入信号');
subplot(2,2,2)
数字信号处理6：IIR滤波器设计


 数字信号处理6：IIR滤波器设计


 数字信号处理6：IIR滤波器设计


 实验六 基于MATLAB的IIR数字滤波器设计


 实验六 基于MATLAB的IIR数字滤波器设计


 IIR滤波器设计之冲激响应不变法与双线性变换法