密码分析学-Enigma机破解

Posted 2023-04-09 Mipiace

密码分析学

Enigma机破解

目录

• 作业要求
• 摘要
• 正文
• • 一：Enigma机加密
  • • 1.1 背景
    • 1.2 加密原理
    • 1.3 安全性分析
    • 1.4 加密算法实现
  • 二：Enigma解密
  • • 2.1 历史上的解密
    • 2.2 Enigma机破解原理
    • • 2.2.1 寻找明密文对关系 -- Ciber
      • 2.2.2 通过环路屏蔽接线板
      • 2.2.3 还原接线板
    • 2.3 解密算法实现

作业要求

（1）给定明文HELLOWORLD，按照以下给定参数，编程实现Enigma机的加密，并输出对应的密文。

• 接线板（6条连线）K1：

  S = [1, 0, 2, 4, 3, 5, 13, 7, 8, 9, 24, 11, 20, 6, 14, 15, 16, 17, 22, 19, 12, 21, 18, 23, 10, 25]

  即a与b相连，d与e相连，g与n相连，k与y相连，m与u相连，s与w相连

• 扰频器组合（固定3个转子，无需从5个中选择3个）

  快速转子QUICK = [0, 18, 24, 10, 12, 20, 8, 6, 14, 2, 11, 15, 22, 3, 25, 7, 17, 13, 1, 5, 23, 9, 16, 21, 19, 4]

  即快速转子的表格中左侧一列为0，1，2，…，25，右侧一列0，18，24，…，4；下同

  中速转子MID = [0, 10, 4, 2, 8, 1, 18, 20, 22, 19, 13, 6, 17, 5, 9, 3, 24, 14, 12, 25, 21, 11, 7, 16, 15, 23]

  慢速转子SLOW = [24, 22, 7, 10, 12, 19, 23, 0, 14, 6, 9, 15, 8, 25, 20, 17, 3, 1, 18, 4, 21, 5, 11, 13, 16, 2]

  各转子起始点K2：(4, 4, 16)

• 反射器

  T = [10, 20, 14, 8, 25, 15, 16, 21, 3, 18, 0, 23, 13, 12, 2, 5, 6, 19, 9, 17, 1, 7, 24, 11, 22, 4]

  即a与k相连，b与u相连，……

（2）给定如下明密文数据流，1）中的快中慢三个转子和反射器的定义不变，尝试恢复密钥K1和K2。

​ 明文：…HELLOWORLD…

​ 密文：…WELLDONEEFGHIJ…

摘要

加密结果：
$$En{c}_{K1,K2}("HELLOWORLD")="MUCDUGWPXB"$$
破解结果：

不考虑未知的字母，未知的字母全部当做没有接线，一共有38个解。python运行时间：8.356976747512817s

格式：[K2, K1]

[[2,14,8],  [0,1,2,13,25,18,19,20,17,9,11,10,12,3,14,15,16,8,5,6,7,21,24,23,22,4]] 
[[2,14,8],  [0,1,2,13,25,23,19,20,8,9,11,10,17,3,14,15,16,12,18,6,7,21,24,5,22,4]] 
[[2,14,8],  [0,1,5,13,25,2,19,20,8,9,11,10,12,3,14,15,16,17,18,6,7,21,24,23,22,4]] 
[[2,14,8],  [0,1,2,13,25,8,19,20,5,9,11,10,12,3,14,15,16,18,17,6,7,21,24,23,22,4]] 
[[2,14,8],  [0,1,2,13,25,12,19,20,8,9,11,10,5,3,14,15,16,23,18,6,7,21,24,17,22,4]] 

此处省略部分，太长了..

[[24,17,3], [0,1,2,3,4,20,24,12,8,17,10,21,7,18,19,22,16,9,13,14,5,11,15,23,6,25]]
[[24,17,3], [0,1,2,3,4,9,24,12,8,5,10,21,7,18,19,22,16,20,13,14,17,11,15,23,6,25]]
[[24,17,3], [5,1,2,3,4,0,24,12,8,9,10,21,7,18,19,22,16,23,13,14,20,11,15,17,6,25]]
[[25,10,6], [0,4,3,2,1,13,8,23,6,9,22,19,12,5,24,15,16,18,17,11,20,21,10,7,14,25]]

正文

一：Enigma机加密

1.1 背景

​   Enigma密码机在1920年代早期开始被用于商业，也被一些国家的军队与政府采用过，在这些国家中，最著名的是第二次世界大战时的纳粹德国。Enigma密码机的大部分设置都会在一段时间（一般为一天）以后被更换。1932年，波兰密码学家马里安·雷耶夫斯基，杰尔兹·罗佐基和亨里克·佐加尔斯基破译了德军的Enigma机，但随后德军对Enigma机进行了改进。波兰战败后，将研究成果分享给英法，随后英国的图灵和其他专家共同破译了Enigma机。

1.2 加密原理

• Enigma密码机的构造

  共由五个主要部件组成。分别是：

1. 包含26个英文字母的键盘： 输入端，每次输入一个英文字母。
2. 线路接线板： 将l对字母相连接，进行加密工作。
3. 扰频组合： 由快速扰频器、中速扰频器、慢速扰频器组成，进行加密工作。
4. 反射器： 保证加密后得到的字母与输入的字母一定不相同。
5. 包含26个英文字母的显示灯的显示灯板： 输出端，在键盘上输入一个英文字母后，灯盘上都会有一个英文字母亮起来，代表明文字母加密后的所对应的密文字母。

• Enigma密码机的加密原理
  ​    Enigma密码机加密是一种多表代换的对称加密算法，逐字母加密。除此之外，Enigma密码机是对称加密，加解密过程一致，不论加密还是解密，

  明文空间：$P\in \mathbb{A}{}^n$，$\mathbb{A}$表示字母表$A-Z$

  密文空间：$C\in \mathbb{A}{}^n$

  秘钥：$K1，K2$，分别表示接线板和三个转子的初始位置

  加解密算法：

  设置好$K1$和$K2$后，明文$P$ 经过：

  ① 标有26个英文字母的线路接线板（$S$）

  ②扰频组合（$R$）

  ③反射器（$T$）

  ④扰频组合（$R^{-1}$）

  ⑤标有26个英文字母的线路接线板($S$)

  得到密文$C$，解密同理。因为加解密算法一致，所以此处不作区分。
  $$\begin{gathered} C=En{c}_{K1,K2}(P) \\ P=En{c}_{K1,K2}(C) \end{gathered}$$

• ​扰频器的作用

​   扰频器也称作转子。单个转子的加密是一种单表置换。转子的左右两侧各有26个点，分别代表A-Z这26个英文字母。一端输入一端输出。为了达到加密的目的，将左右两侧的字母交叉连接，例如：转子左侧的字母A并不与转子右侧的A相连，而是与字母E相连，即表示字母A经过扰频器的加密后变成了字母E。

​   因为这种单个转子提供的密码表是固定不变的，加密出来的密文比较容易被破解,因此选择三个转子串联在一起从而达到加密的目的。
三个转子被串联后，输入的字母经过这三个转子被进行多次替换。如果转子不转，那么输入的字母不论经过几个串联的转子，最终得到的依旧是一个固定的密码表，安全性依旧不高。因此为了提高加密的安全性，每输入一个字母后，第一个转子就会自动转动一格。当第一个转子转动一圈后，第二个转子就转动一格。同理，第二个转子转动一圈后，第三个转子转动一格。这样原来的单表置换经过旋转变为多表置换，使得安全性更高。

​   根据$Kerckhoffs$假设，加密算法的内部结构是公开的，也就是说转子的内部结构对于加解密双方来说是一致的。秘钥$K2$ 包含的是转子的排列方式和初始位置，如果有n个转子，选用m个进行加密，秘钥空间为
$$|K2|=A_n^m\ast 26^3$$
​   对于只有三个转子的Enigma机，密钥空间只有$3!\ast 26^3=105456$，这种级别的安全性是不够的，这时候接线板$K1$就起了关键作用。我们会在安全性分析中做解释。

• ​​反射器作用

​   反射器的加密是一种固定的单表置换（这里的单表置换是自定义的，无密钥）。加密方式是将最后一个转子的其中两个触点连接起来，并将电流沿一个不同的路倒回到线路接线板。这样的反射器导致加密后的字母与输入字母一定不相同，并且使得Enigma密码机的加密过程是自反的，这也是加解密一致的关键部件。同时还让Enigma机有了另一个性质，即：一个字母不会加密成自身。这也是后面破解的关键。

1.3 安全性分析

​    我们说过，Enigma机的本质是一种多表替换，我们之前学习过的凯撒密码和维吉尼亚密码也是替换密码，但后两种密码我们知道会有字母频率的漏洞。主要因为他们的加密都是使用的同一张密码表，而Enigma机每加密一个字母，就会转动一下，相当于换了一张密码表，基本可以做到加密一个字母就更换一次密码表并且不重复。

​   没有了字母频率攻击的“后顾之忧”，那我们再考虑暴力破解：

​   我们在前面讨论过对于3个转子的Enigma机，他的转子排列和初始位置的组合$K2$只有105456大小。这显然不够，我们来考虑接线板（$K1$）的作用。26个字母，有 $t$ 根连线，那么就有
$$\frac{26!}{(26-t)!\ast t!\ast 2^t}$$
种接线方式，如果有6根接线，$t=6$，那么K1就有
$$|K1|=\frac{26!}{(26-6)!\ast 6!\ast 2^6}=70,605,879,373,725,696,000\approx 7\ast 10^{20}$$
总密钥空间大小：
$$|K1|\ast |K2|=A_5^3\ast 26^3\ast \frac{26!}{(26-6)!\ast 6!\ast 2^6}=4,236,352,762,423,541,760,000\approx 4\ast 10^{22}$$
​    可以看到接线板对整体密钥空间的扩大起重要作用。二战时期没有高速计算机，通过人工穷举密钥，对于这种数量级的密钥空间是不现实的。即使是使用计算机进行穷举，大部分电脑的单秒运算量在10的七次方到10的九次方之间，我们假设每秒穷举$10^9$个密钥为例，筛选出正确密钥的期望时间约为$400000$年。

​    除此之外，德军在使用Enigma机时还规定了一定的操作流程，他们在通信时，会先使用日秘钥加密一个会话秘钥，然后使用会话秘钥来加密明文。会话秘钥也是三个字母，德军先使用日秘钥加密会话秘钥两次，然后将这6个字母发送出去。比如日秘钥ABC，会话秘钥QWE，那么$QWEQWE\stackrel{ABC}{⟶}DCYXEV$，加密两边是为了防止出现错误。德军本意是为了保证每条信息都是用不同的密钥进行加密的，避免了使用同一个密钥加密过多内容而被破解者找到破绽。但是波兰人便是从这六个字母中找到了规律，实现了的初步的破解。但波兰的破解是不具有普遍性的，德军改进Enigma机和操作流程后便失效了。

1.4 加密算法实现

​ 这里我们用一个具体的字母举例，待加密字符为 ‘H’，K1,K2为题目所给，看一下加密算法的具体实现过程：

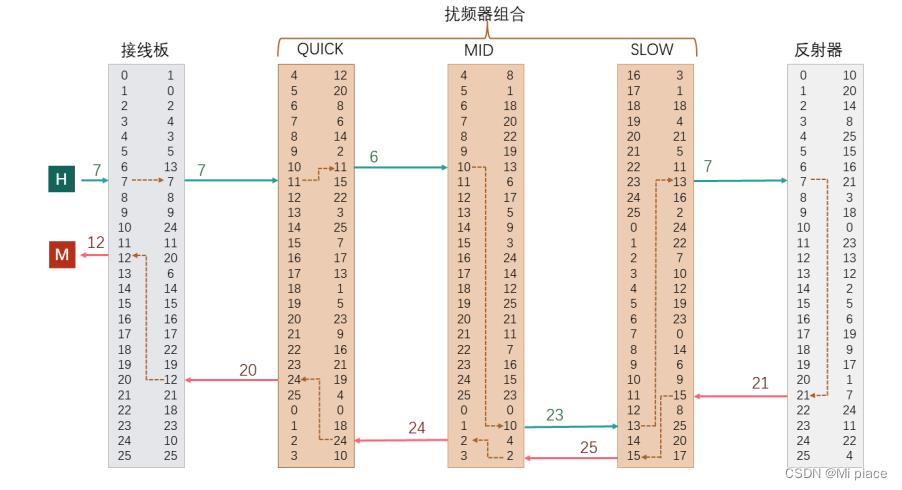
1. 接线板K1

在键盘上输入字母H（7），H首先经过接线板（Stecker），发现H没有与其它字母相连，所以经过接线板后明文没有发生变化，仍为H（7）。

2. 正向扰频器组合（Rotors）

首先通过密钥K2（4,4,16）将转子转动到相应位置。再将H（7）分别通过这三个转子。

H对应位置为7，将7作为输入通过快速转子，找到此时的第7个位置对应的左侧数字为11，再找到右侧对应的11，位置为6，所以经过快速转子，输出变为6。然后再以位置6作为输入通过中速转子，此时位置6对应的左侧数字为10，找到右侧对应的10，位置为23，经过中速转子，输出变为23。再将23作为输入通过慢速转子，位置23对应的左侧数字为13，找到右侧对应的13，位置为7。经过慢速转子，输出变为7。

3. 反射器

正向扰频器输出的结果为7，将7作为输入通过反射器，输出结果为21。

4. 逆向扰频器组合

将上一步的结果21作为输入先通过慢速转子，此时位置21对应的右侧数字为15，找到左侧对应的15，位置为25。同理，再依次通过中速转子输出变为24，最后通过快速转子输出变为20。

5. 接线板K1

将20作为输入，通过逆向线路接线板，得到输出为12，对应字母为M。

最终M作为最终结果在显示灯板上显示出来。同理，可以对E进行类似的加密得到U。

关键函数：

'''（整体被包装在类中，完整代码见压缩包 my_Enigma.py ）'''

def Encode_Decode(self,inputtext='',K2 = []):   
    if K2: 
        '''可以通过显式提供K2来设置enigma机，K1一般不改变，只能通过self.SET函数设置'''
        self.SET(K2)
    if inputtext.isalpha():
        outputtext = ""
        inputtext = inputtext.lower()
        for ch in inputtext:
            tmp = ord(ch)-97
            '''通过接线板'''
            tmp = self.K1[tmp]
            '''通过三个转子'''     
            tmp = (Cog_quick_re[(tmp + self.offset[0])% 26] - self.offset[0] + 26)%26 
            tmp = (Cog_mid_re[(tmp + self.offset[1])% 26] - self.offset[1] + 26)%26
            tmp = (Cog_slow_re[(tmp + self.offset[2])% 26] - self.offset[2] + 26)%26
            '''通过反射器'''
            tmp = T[tmp]
            '''通过三个轮子的逆'''
            tmp = (Cog_slow[(tmp + selfpackage egnima;
import java.util.Scanner;
public class enigma 
static public void main(String []args)

Scanner cin=new Scanner(System.in);
System.out.print("Input 0 to encode message and 1 to decode message:");
int op=cin.nextInt();
if(op==0)
encode();
	else
	decode();

static void encode()

	String msg="";
	String encodemsg="";
	int count=0;
	System.out.printf("%s","Input the message:");
	Scanner cin=new Scanner(System.in);
	msg=cin.nextLine();
	for(int i=0;i<msg.length();i++)
	
if((Character.isSpace(msg.charAt(i))))

			encodemsg+=" ";
		

		else if((msg.charAt(i)-count)<'a')
		
		encodemsg+=(char)(msg.charAt(i)+26-count);
		
		else
		encodemsg+=(char)(msg.charAt(i)-count);
		
		count++;
	
	System.out.println(decodemsg);

static void decode()

	
	String msg="";
	String decodemsg="";
	int count=0;
	System.out.printf("%s","Input the message:");
	Scanner cin =new Scanner(System.in);
	msg=cin.nextLine();
	for(int i=0;i<msg.length();i++)
	
		if(Character.isSpace(msg.charAt(i)))
			decodemsg+=" ";
		else if(msg.charAt(i)+count>'z')
			decodemsg+=(char)(msg.charAt(i)-26+count);
			else
			decodemsg+=(char)(msg.charAt(i)+count);
		count++;
	
	System.out.println(decodemsg);