点过程及其性质介绍(Point Processes)
Posted Jie Qiao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了点过程及其性质介绍(Point Processes)相关的知识,希望对你有一定的参考价值。
我们会在很多地方遇到事件类型的数据,比如日志,金融,用户活动等场景。点过程是一类对这种事件类型建模的重要工具。要介绍点过程,我们可以从泊松过程,以及泊松分布讲起。
泊松分布的含义
该部分参考了 马同学的文章:泊松分布的现实意义是什么,为什么现实生活多数服从于泊松分布?。
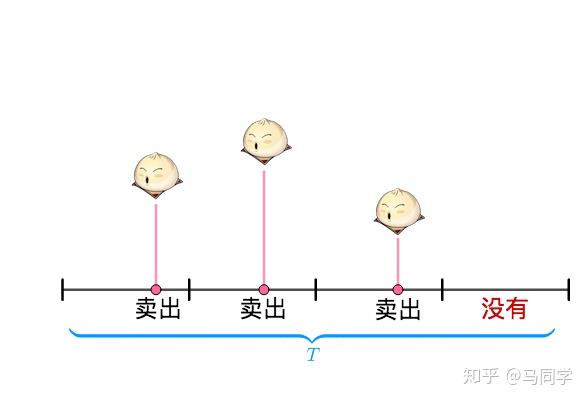
我们可以将时间划分为一个区间,假设每个区间只会发生1次和0次,那么就服从二项分布。如果我们想知道在这个区间内,卖出3个馒头的概率,就和抛了4次硬币(4个时间段),其中3次正面(卖出3个)的概率一样了。
此时概率为:
C 4 3 p 3 ( 1 − p ) 1 C^3_4 p^3 (1-p)^1 C43p3(1−p)1
然而,由于区间很大,很可能同时发生两次,为了避免这一问题,我们可以将区间划分数量设为无穷个,于是这个概率变成:
lim n → ∞ C n k p k ( 1 − p ) n − k \\lim _n\\rightarrow \\infty C^k_n p^k (1-p)^n-k n→∞limCnkpk(1−p)n−k
那么p怎么求呢?因为二项分布中 E ( X ) = n p = μ \\displaystyle E( X) =np=\\mu E(X)=np=μ。换句话说,如果我们抛4次硬币,并期望能够发生3次的话,对应的概率应该为, 3 4 \\displaystyle \\frac34 43,类似的,我们抛n次硬币,期望发生3次,那么只要设 p = 3 n \\displaystyle p=\\frac3n p=n3就能达到这个效果。因此:
p = μ n p=\\frac\\mu n p=nμ
于是
lim n → ∞ C n k p k ( 1 − p ) n − k = lim n → ∞ C n k ( μ n ) k ( 1 − μ n ) n − k \\lim _n\\rightarrow \\infty C^k_n p^k (1-p)^n-k =\\lim _n\\rightarrow \\infty C^k_n\\left(\\frac\\mu n\\right)^k\\left( 1-\\frac\\mu n\\right)^n-k n→∞limCnkpk(1−p)n−k=n→∞limCnk(nμ)k(1−nμ)n−k
lim
n
→
∞
C
n
k
(
μ
n
)
k
(
1
−
μ
n
)
n
−
k
=
lim
n
→
∞
n
(
n
−
1
)
(
n
−
2
)
⋯
(
n
−
k
+
1
)
k
!
μ
k
n
k
(
1
−
μ
n
)
n
−
k
=
lim
n
→
∞
μ
k
k
!
n
n
⋅
n
−
1
n
⋯
n
−
k
+
1
n
(
1
−
μ
n
)
−
k
(
1
−
μ
n
)
n
\\beginaligned \\lim _n\\rightarrow \\infty C^k_n\\left(\\frac\\mu n\\right)^k\\left( 1-\\frac\\mu n\\right)^n-k & =\\lim _n\\rightarrow \\infty \\fracn(n-1)(n-2)\\cdots (n-k+1)k!\\frac\\mu ^kn^k\\left( 1-\\frac\\mu n\\right)^n-k\\\\ & =\\lim _n\\rightarrow \\infty \\frac\\mu ^kk!\\fracnn \\cdot \\fracn-1n \\cdots \\fracn-k+1n\\left( 1-\\frac\\mu n\\right)^-k\\left( 1-\\frac\\mu n\\right)^n \\endaligned
n→∞limCnk(nμ)k(1−nμ)n−k=n→∞limk!n(n−1)(n−2)⋯(n−k+1)nkμk(1−nμ)n−k=n→∞limk!μknn⋅nn−1⋯nn−k+1(1−nμ)−k(1−nμ)n
其中
lim n → ∞ n n ⋅ n − 1 n ⋯ n − k + 1 n ( 1 − μ n ) − k = 1 \\lim _n\\rightarrow \\infty \\fracnn \\cdot \\fracn-1n \\cdots \\fracn-k+1n\\left( 1-\\frac\\mu n\\right)^-k =1 n→∞limnn⋅nn−1⋯nn−k+1(1−nμ)−k=1
lim n → ∞ ( 1 − μ n ) n = e − μ \\lim _n\\rightarrow \\infty \\left( 1-\\frac\\mu n\\right)^n =e^-\\mu n→∞lim以上是关于点过程及其性质介绍(Point Processes)的主要内容,如果未能解决你的问题,请参考以下文章