POJ 3693 Maximum repetition substring(后缀数组[重复次数最多的连续重复子串])

Posted 2022-11-27 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

题集链接→2008 Asia Hefei Regional Contest Online by USTC

 POJ 3693 Maximum repetition substring

Accept: 0    Submit: 0
Time Limit: 1000 MS    Memory Limit : 65536 K

 Problem Description

The repetition number of a string is defined as the maximum number R such that the string can be partitioned into R same consecutive substrings. For example, the repetition number of "ababab" is 3 and "ababa" is 1.

Given a string containing lowercase letters, you are to find a substring of it with maximum repetition number. 

 Input

The input consists of multiple test cases. Each test case contains exactly one line, which gives a non-empty string consisting of lowercase letters. The length of the string will not be greater than 100,000.

The last test case is followed by a line containing a '#'.

 Output

For each test case, print a line containing the test case number( beginning with 1) followed by the substring of maximum repetition number. If there are multiple substrings of maximum repetition number, print the lexicographically smallest one.

 Sample Input

ccabababc
daabbccaa
#

 Sample Output

Case 1: ababab
Case 2: aa

 Problem Idea

解题思路:

【题意】

给定一个字符串，要求输出重复次数最多的连续重复子串

若有多个连续重复子串的重复次数相同，输出字典序最小的一个

【类型】
后缀数组[重复次数最多的连续重复子串]
【分析】

此题是一道关于求重复次数最多的连续重复子串的后缀数组变形题((～￣▽￣)～说它是变形题也仅仅是因为多了输出字典序最小的连续重复子串)

首先，和求裸的重复次数最多的连续重复子串的后缀数组题一样

"重复次数最多的连续重复子串"解法(摘自罗穗骞的国家集训队论文):

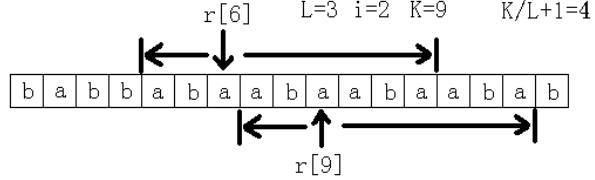
先穷举长度L，然后求长度为L的子串最多能连续出现几次。首先连续出现1次是肯定可以的，所以这里只考虑至少2次的情况。假设在原字符串中连续出现2次，记这个子字符串为S，那么S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和
往后各能匹配到多远，记这个总长度为K，那么这里连续出现了K/L+1次。最后看最大值是多少。如图所示。

穷举长度L的时间是n，每次计算的时间是n/L。所以整个做法的时间复杂度是O(n/1+n/2+n/3+……+n/n)=O(nlogn)。
ps：基本思路在罗穗骞的论文里已经说得比较清楚了，而我在这里要提的是论文里比较模糊的部分
要提一提的总共有两点，第一点比较显而易见
“S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个”
由于当前S是有两个长度为L的连续重复子串拼接而成的，那意味着S[i]和S[i+L](0≤i<L)必定是一样的字符
而这两个字符位置相差L
而字符r[0],r[L],r[L*2],r[L*3],......中相邻两个的位置差均为L
“只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远”，对于往后能匹配到多远，这个直接根据最长公共前缀就能很容易得到，即上图中的后缀Suffix(6)和后缀Suffix(9)的最长公共前缀。而对于往前能匹配到多远，我们当然可以一开始就把字符串反过来拼在后面，这样也能根据最长公共前缀来看往前能匹配到多远，但这样效率就比较低了。
其实，当枚举的重复子串长度为i时，我们在枚举r[i*j]和r[i*(j+1)]的过程中，必然可以出现r[i*j]在第一个重复子串里，而r[i*(j+1)]在第二个重复子串里的这种情况，如果此时r[i*j]是第一个重复子串的首字符，这样直接用公共前缀k除以i并向下取整就可以得到最后结果。但如果r[i*j]如果不是首字符，这样算完之后结果就有可能偏小，因为r[i*j]前面可能还有少许字符也能看作是第一个重复子串里的。
于是，我们不妨先算一下，从r[i*j]开始，除匹配了k/i个重复子串，还剩余了几个字符，剩余的自然是k%i个字符。如果说r[i*j]的前面还有i-k%i个字符完成匹配的话，这样就相当于利用多余的字符还可以再匹配出一个重复子串，于是我们只要检查一下从r[i*j-(i-k%i)]和r[i*(j+1)-(i-k%i)]开始是否有i-k%i个字符能够完成匹配即可，也就是说去检查这两个后缀的最长公共前缀是否比i-k%i大即可。
当然如果公共前缀不比i-k%i小，自然就不比i小，因为后面的字符都是已经匹配上的，所以为了方便编写，程序里面就直接去看是否会比i小就可以了。

然后，当有多个重复次数相同的连续重复子串时，需输出字典序最小的

我们知道后缀数组sa[]就是根据字典序大小来排序的，故可以借用sa[]数组找出最先符合重复次数的子串即为所求

输出子串可以通过在要输出的段的末尾赋为'\\0'，这样只要printf时调输出段的开头就可以了，因为'\\0'人工标记了字符串结束

【时间复杂度&&优化】
O(nlogn)

题目链接→POJ 3693 Maximum repetition substring

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 5005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
const int MAXN = 100005;
//rnk从0开始
//sa从1开始,因为最后一个字符(最小的)排在第0位
//height从1开始,因为表示的是sa[i - 1]和sa[i]
//倍增算法 O(nlogn)
int wa[MAXN], wb[MAXN], wv[MAXN], ws_[MAXN];
//Suffix函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数,如果原序列都是字母可以直接取128,如果原序列本身都是整数的话,则m可以取比最大的整数大1的值
//待排序的字符串放在r数组中,从r[0]到r[n-1]，长度为n
//为了方便比较大小,可以在字符串后面添加一个字符,这个字符没有在前面的字符中出现过,而且比前面的字符都要小
//同上,为了函数操作的方便,约定除r[n-1]外所有的r[i]都大于0,r[n-1]=0
//函数结束后,结果放在sa数组中,从sa[0]到sa[n-1]
void Suffix(int *r, int *sa, int n, int m)

    int i, j, k, *x = wa, *y = wb, *t;
    //对长度为1的字符串排序
    //一般来说,在字符串的题目中,r的最大值不会很大,所以这里使用了基数排序
    //如果r的最大值很大,那么把这段代码改成快速排序
    for(i = 0; i < m; ++i) ws_[i] = 0;
    for(i = 0; i < n; ++i) ws_[x[i] = r[i]]++;//统计字符的个数
    for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1];//统计不大于字符i的字符个数
    for(i = n - 1; i >= 0; --i) sa[--ws_[x[i]]] = i;//计算字符排名
    //基数排序
    //x数组保存的值相当于是rank值
    for(j = 1, k = 1; k < n; j *= 2, m = k)
    
        //j是当前字符串的长度,数组y保存的是对第二关键字排序的结果
        //第二关键字排序
        for(k = 0, i = n - j; i < n; ++i) y[k++] = i;//第二关键字为0的排在前面
        for(i = 0; i < n; ++i) if(sa[i] >= j) y[k++] = sa[i] - j;//长度为j的子串sa[i]应该是长度为2 * j的子串sa[i] - j的后缀（第二关键字）,对所有的长度为2 * j的子串根据第二关键字来排序
        for(i = 0; i < n; ++i) wv[i] = x[y[i]];//提取第一关键字
        //按第一关键字排序 (原理同对长度为1的字符串排序)
        for(i = 0; i < m; ++i) ws_[i] = 0;
        for(i = 0; i < n; ++i) ws_[wv[i]]++;
        for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1];
        for(i = n - 1; i >= 0; --i) sa[--ws_[wv[i]]] = y[i];//按第一关键字,计算出了长度为2 * j的子串排名情况
        //此时数组x是长度为j的子串的排名情况,数组y仍是根据第二关键字排序后的结果
        //计算长度为2 * j的子串的排名情况,保存到数组x
        t = x;
        x = y;
        y = t;
        for(x[sa[0]] = 0, i = k = 1; i < n; ++i)
            x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j]) ? k - 1 : k++;
        //若长度为2 * j的子串sa[i]与sa[i - 1]完全相同,则他们有相同的排名
    

int Rank[MAXN], height[MAXN], sa[MAXN], r[MAXN];
void calheight(int *r,int *sa,int n)

    int i,j,k=0;
    for(i=1; i<=n; i++)Rank[sa[i]]=i;
    for(i=0; i<n; height[Rank[i++]]=k)
        for(k?k--:0,j=sa[Rank[i]-1]; r[i+k]==r[j+k]; k++);

int n,minnum[MAXN][17];
void RMQ()   		//预处理  O(nlogn)

	int i,j;
	int m=(int)(log(n*1.0)/log(2.0));
	for(i=1;i<=n;i++)
		minnum[i][0]=height[i];
	for(j=1;j<=m;j++)
		for(i=1;i+(1<<j)-1<=n;i++)
			minnum[i][j]=min(minnum[i][j-1],minnum[i+(1<<(j-1))][j-1]);

int Ask_MIN(int a,int b) 	//O(1)

	int k=int(log(b-a+1.0)/log(2.0));
	return min(minnum[a][k],minnum[b-(1<<k)+1][k]);

int calprefix(int a,int b)

    a=Rank[a],b=Rank[b];
    if(a>b)
        swap(a,b);
    return Ask_MIN(a+1,b);

char s[MAXN];
int q[MAXN];
int main()

    int i,j,k,ans,Max,cnt,p=1;
    bool flag;
    while(scanf("%s",s)&&s[0]!='#')
    
        n=strlen(s);
        Max=0;
        for(i=0;s[i]!='\\0';i++)
            r[i]=s[i]-'a'+1;
        r[i]=0;
        Suffix(r,sa,n+1,27);
        calheight(r,sa,n);
        RMQ();
        for(i=1;i<=n;i++)
        
            for(j=0;j+i<n;j+=i)
            
                ans=calprefix(j,j+i);
                k=j-(i-ans%i);
                ans=ans/i+1;
                if(k>=0&&calprefix(k,k+i)>=i)
                    ans++;
                //printf("L=%d,R=%d\\n",i,ans);
                if(Max<ans)
                    Max=ans,cnt=0,q[cnt++]=i;
                else if(Max==ans&&i!=q[cnt-1])
                    q[cnt++]=i;
            
        
        for(flag=false,i=1;i<=n&&!flag;i++)
            for(j=0;j<cnt&&!flag;j++)
                if(calprefix(sa[i],sa[i]+q[j])>=q[j]*(Max-1))
                
                    s[sa[i]+q[j]*Max]='\\0';
                    flag=true;
                    printf("Case %d: %s\\n",p++,s+sa[i]);
                
    
    return 0;

菜鸟成长记