C++线性筛——筛质数详解

Posted 2023-04-08 不怕困难的博客

什么是质数

质数也叫素数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

怎么判断质数

 具体代码如下：

bool primes(int x) 
	int cnt = 0;//计数，看看从1到x有多少个因数
	for(int i = 1; i <= x; i++) 
		if(x % i == 0) cnt++;//如果x%i==0，代表i是x的因数，计数器加1
	
	if(cnt == 2) return true;//如果有且只有两个因数，那么x是质数，否则不是。
	else return false;

稍加修改就可以减少很多时间复杂度。

代码如下：

bool primes(int x) 
	for(int i = 2; i <= x - 1; i++) 
		if(x % i == 0) return false;
	
	return true;

根据因数的性质，可以再优化：

bool primes(int x) 
	for(int i = 2; i <= sqrt(x); i++) 
		if(x % i == 0) return false;
	
	return true;

如何筛质数

埃筛法（不必要知道埃筛，时间复杂度高）会重复筛掉一些，如质数2会筛6，而3也会筛6，这就慢了许多，那么我们可不可以只筛一次呢，办法是有的，就是只筛这个合数的最小质因数

做法

1.依次枚举每一个数
2.若当前数没被筛，则把这个数加入质数集合
3.对于每一个数，枚举当前已知质数，并相应筛掉当 前 数 × 枚 举 到 的 质 数 当前数 \\times 枚举到的质数当前数×枚举到的质数，而被筛掉的那个数的最小质因数一定是枚举到的质数(为什么看后面)
4.如果i是枚举到的质数的倍数，停止枚举质数
代码如下：

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉
void get_primes(int n)

    for (int i = 2; i <= n; i ++ )
    
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        
    

例题

1292. 哥德巴赫猜想

哥德巴赫猜想的内容如下：

任意一个大于 44 的偶数都可以拆成两个奇素数之和。

例如：

8=3+5
20=3+17=7+13
42=5+37=11+31=13+29=19+23

现在，你的任务是验证所有小于一百万的偶数能否满足哥德巴赫猜想。

输入格式

输入包含多组数据。

每组数据占一行，包含一个偶数 n。

读入以 0 结束。

输出格式

对于每组数据，输出形如 n = a + b，其中 a,b 是奇素数。

若有多组满足条件的 a,b，输出 b−a 最大的一组。

若无解，输出 Goldbach's conjecture is wrong.。

数据范围

6≤n<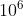

输入样例：

8
20
42
0

输出样例：

8 = 3 + 5
20 = 3 + 17
42 = 5 + 37

就是线性筛的模板题：

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
int primes[N], cnt;
bool st[N];
void init(int n) 
	for(int i = 2; i <= n; i++) 
		if(!st[i]) primes[cnt++] = i;
		for(int j = 0; primes[j] * i <= n; j++) 
			st[primes[j] * i] = true;
			if(i % primes[j] == 0) break;
		
	

int main() 
	init(N - 1);
	int n;
	while(cin >> n, n) 
		for(int i = 1; ; i++) 
			int a = primes[i];
			int b = n - a;
			if(!st[b]) 
				printf("%d = %d + %d\\n", n, a, b);
				break;
			
		
	
	return 0;

线性筛

除了处理质数的问题，线性筛还可以较为高效的处理数论函数，虽然有杜教筛这个东西，关键的时候还是要线性筛救命

1.筛质数

先看看线性筛本体，它的功能是判断质数，以及求最小质因数

1.记录minfactor,prime

2.对cur一直用prime数组筛去剩下的合数

这里判断质数的标准很简单，就是判断一个数的最小质因数是否就是它本身

由于是求最小质因数，(prime[j]<=minfact[i]),这样可以证明每个合数仅被它的最小质因数筛到，保证线性复杂度

2.求(phi(n))

(phi(p)=p-1),利用这个性质，可在判断质数的同时筛出它的欧拉函数

由欧拉函数的积性性得,(phi(mn)=phi(m)phi(n))

当(minfact[i]=prime[j]),即有重复质因子时，(phi(p^k)=p^{k-1}(p-1)),乘上p即可

不然乘上(p-1)

3.求(mu(n))

(mu(p)=-1),利用这个性质，可在判断质数的同时筛出它的莫比乌斯函数

当(minfact[i]=prime[j]),即有重复质因子时，(mu(n)=0)

不然乘上(mu(n)=-mu(i))

4.求(d(n))

比前面的两个函数要麻烦一些，求(d(n))要记录n中最小质因子数(cnt[n])

对于质数,(cnt[n])很显然等于1

接着考虑(d(n)),(n=Pi^k_{i=1}p_i^{a_i}),(d(n)=Pi^k_{i=1}(p_i+1))

如果(minfact[i]=prime[j]),由牛顿二项式定理得，(d(n)=d(i)/(cnt[i]+1)*(cnt(i)+2))

不然(d(n)=d(i)*d(prime[j]))

5.求(sigma(n))

类似于求(d(n)),不过这次要记录一个数组(sum[i]=Sigma_{i=0}^kp^i),p表示n的最小质因数，(sum[i])表示最小质因数的k次幂下的和

对于质数，(sum[i])很显然等于p+1

接着考虑(sigma(n)),(sigma(n)=Pi_{i=1}^kSigma_{j=0}^{a_i}p^j_i)

如果(minfact[i]=prime[j]),在求和式中加入一项(p^{k+1}),等同于乘((sum[i]*p+1)/sum[i])

不然(sigma(n)=sigma(i)*sigma(prime[j]))

可以发现，所有上述求数论函数的方法都依靠他们的积性性，并通过每个数的最小质因数来确定计算方法

能用原本判断质数的线性筛求数论函数就是利用了对最小质因数的分析

虽然杜教筛不算很难，但线性筛好写好想，功能全面，不失为一个很好的备用方案