详谈数据结构与算法

Posted 2022-11-27 涤生大数据

1.为什么需要学习算法？

       程序员校招社招到底该面不面算法题？该如何准备？_涤生大数据的博客-CSDN博客

2.数据结构与算法的关系

        很多人在开始接触编程时都会经历面向对象、数据结构，再到刷算法题，但是很多人其实并未理清楚数据结构和算法的关系是什么。本文会就这一问题聊聊数据结构和算法之间的关系。

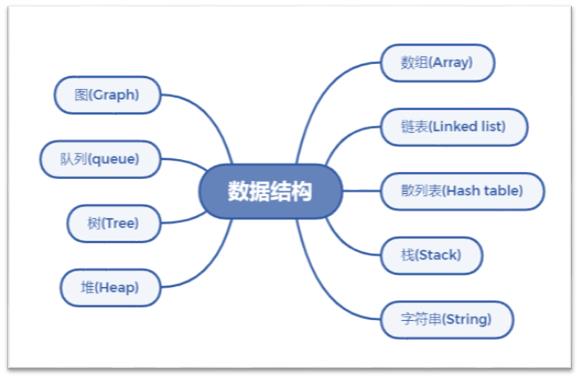
        数据结构简单来讲就是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成 。常用的数据结构如上图，其中本文将字符串单独作为一种数据结构是因为大家在笔试、面试中会经常遇到对于该知识点的基本考法（非常简单，必拿）。

        熟知数据结构是开起算法之路的必经站点。它是计算机中存储、组织数据的方式，主要包含元素之间的逻辑关系、存储关系和操作三部分。并且，对于不同的数据结构，其数据存储方式是不同的，这也就解释了为什么数据库的实现大都依赖数结构，而计算机网络会依赖表结构。由这些基本数据结构所实现的业务应用就是对算法的探索和优化。

        按一定的逻辑结构，把数据组织起来，并选择适当的存储表示方法把逻辑结构组织好的数据存储到计算机的存储器里是数据结构实现的。而算法实现的目的是为了更有效的处理数据，提高数据运算效率。算法是指用来操作数据、解决程序问题的一组方法。算法的分类大概如下(若有遗漏，请大家补全哈)

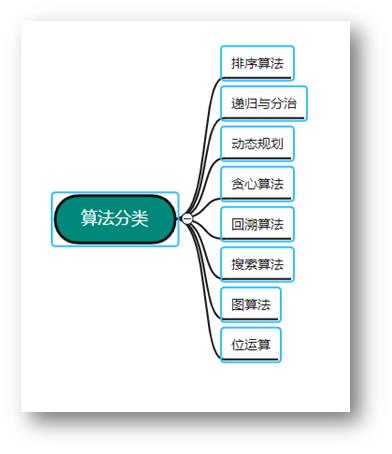
        为什么有这么多的数据结构和算法出现？随着互联网行业的发展，应用程序的越来越复杂、数据种类繁多、数据量庞大，百万、亿级别。这样会使得程序执行、数据处理变得很慢，设置无法执行。数据结构和算法就是来解决这些问题的。

        问题又来了，它们凭什么可以改善这些问题呢？首先，不同的数据结构凭借其不同的存储方式，可以最优的适用于各种不同的业务需要。其次，经过这么多年的发展，相信都知道时间复杂度和空间复杂度这两个重点概念，我们在实际的代码开发中，都会考虑到这两者的更佳值（同一个场景下，业务逻辑不变的情况下，调整代码逻辑，使其执行速度更快，资源消耗更少）。最后，就是要感谢机器硬件配置的改善，这种发展是与时俱进的，极大地改善了代码的运行效率和环境。

        对于同一个问题，使用不同的算法，也许最终得到的结果是一样的，但在过程中消耗的资源和时间却会有很大的区别。

时间复杂度：是指执行当前算法所消耗的时间，通常用「时间复杂度」来描述。
空间复杂度：是指执行当前算法需要占用多少内存空间，通常用「空间复杂度」来描述。

在这里举个例子简单介绍下二者的计算方法：

1.   时间复杂度

        时间复杂度并不是将算法程序运行的时间作为衡量值，这种方法容易受运行环境的影响，在性能高的机器上跑出来的结果与在性能低的机器上跑的结果相差会很大。而且对测试时使用的数据规模也有很大关系。并且，我们在写算法的时候，还没有办法完整的去运行对吧。

        所以，我们假设算法的问题规模为n，那么操作单元数量便用函数f(n)来表示，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这就是算法复杂度的计算方法。

一些具有迷惑性的例子：

	 
void hello (int n)
    for( int sz = 1 ; sz < n ; sz += sz )
        for( int i = 1 ; i < n ; i ++ )
            cout << "Hello" << endl;

上面这段代码的时间复杂度是 O(nlog n) 而不是 O(n^2)

	
bool isPrime (int n)
    for( int x = 2 ; x * x <= n ; x ++ )
        if( n % x == 0 )
            return false;
    return true;

上面这段代码的时间复杂度是 O(sqrt(n)) 而不是 O(n)。

        再举一个例子，有一个字符串数组，将数组中的每一个字符串按照字母序排序，之后再将整个字符串数组按照字典序排序。两步操作的整体时间复杂度是多少呢？

        如果回答是 O(n*nlog n + nlog n) = O(n^2log n)，这个答案是错误的。字符串的长度和数组的长度是没有关系的，所以这两个变量应该单独计算。假设最长的字符串长度为 s，数组中有 n 个字符串。对每个字符串排序的时间复杂度是 O(slog s)，将数组中每个字符串都按照字母序排序的时间复杂度是 O(n * slog s)。

        将整个字符串数组按照字典序排序的时间复杂度是 O(s * nlog n)。排序算法中的 O(nlog n) 是比较的次数，由于比较的是整型数字，所以每次比较是 O(1)。但是字符串按照字典序比较，时间复杂度是 O(s)。所以字符串数组按照字典序排序的时间复杂度是 O(s * nlog n)。所以整体复杂度是 O(n * slog s) + O(s * nlog n) = O(n*slog s + s*nlogn) = O(n*s*(log s + log n)) = O(n*s*log(n*s)）。

        常见的时间复杂度量级有：O(1)、O(logN)、O(n)、O(nlogN)、O(n²)、O(n³)、O(n^k)、(2^n)等。

一些示例及经验（代码）：

1.O(n^2) 算法可以处理 10^4 级别的数据规模(保守估计，处理 1000 级别的问题肯定没问题)；
2.O(n) 算法可以处理 10^8 级别的数据规模(保守估计，处理 10^7 级别的问题肯定没问题) ；
3.O(nlog n) 算法可以处理 10^7 级别的数据规模(保守估计，处理 10^6 级别的问题肯定没问题)。

2.   空间复杂度

        时间复杂度不是用来计算程序具体耗时的，那么空间复杂度也不是用来计算程序实际占用的空间的。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势，我们用 S(n) 来定义。

空间复杂度比较常用的有：O(1)、O(n)、O(n²)，我们下面来看看：

        递归调用是有空间代价的，递归算法需要保存递归栈信息，所以花费的空间复杂度会比非递归算法要高。

int sum( int n )
    assert( n >= 0 )
    int ret = 0;
    for ( int i = 0 ; i <= n ; i ++ )
        ret += i;
    return ret;

上面算法的时间复杂度为 O(n)，空间复杂度 O(1)。

int sum( int n )
    assert( n >= 0 )
    if ( n == 0 )
        return 0;
    return n + sum( n - 1 );

上面算法的时间复杂度为 O(n)，空间复杂度 O(n)。

3总体分类

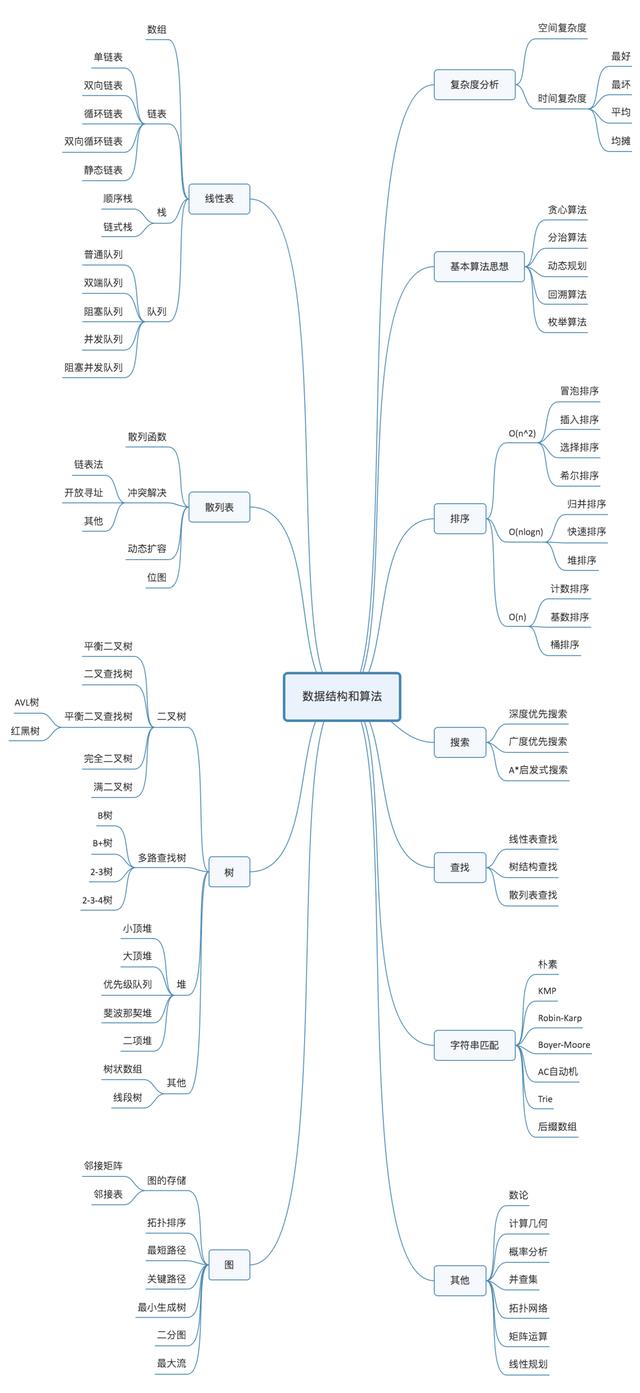
学习小总结

        大家在初学这些的时候不需要太关注时间复杂度和空间复杂度，需要重点学习数据结构的几个分类，其存储方式、使用场景和优缺点。当有一定积累的时候，再去关注优化方面（后续的算法题也会有讲解哈），本周第一节课大家只需要掌握这么多就行了哈