kotlin学习笔记之尾递归优化（tailrec）

Posted 2022-11-27 mictoy_朱

尾递归

递归：adj recursive；尾递归：Tail Recursion

• 递归的一种特殊形式
• 调用自身后无其他操作
• tailrec关键字提示编译器尾递归优化

示例代码

data class ListNode(val value:Int,var next:ListNode? = null)

fun findListNode(head:ListNode?,value:Int):ListNode? //定义一个递归函数
    head?:return null
    if (head.value == value) return head
    return findListNode(head.next,value)    //return除了调用自己，没有多余的操作，所以是尾递归


fun main() 
    val NODE_COUNT = 4

    val rootNode:ListNode? = ListNode(0)    //定义一个rootNode
    var p = rootNode
    for (i in 1..NODE_COUNT)       //循环生成10个node
        p?.next = ListNode(i)
        p = p?.next
    
    var p2 = rootNode
    while (p2 != null)     //打印检查node
        println(p2.toString())
        p2 = p2.next
    

    println(findListNode(rootNode,NODE_COUNT-2)?.toString())

运行结果：

ListNode(value=0, next=ListNode(value=1, next=ListNode(value=2, next=ListNode(value=3, next=ListNode(value=4, next=null)))))
ListNode(value=1, next=ListNode(value=2, next=ListNode(value=3, next=ListNode(value=4, next=null))))
ListNode(value=2, next=ListNode(value=3, next=ListNode(value=4, next=null)))
ListNode(value=3, next=ListNode(value=4, next=null))
ListNode(value=4, next=null)
ListNode(value=2, next=ListNode(value=3, next=ListNode(value=4, next=null)))

这里尚未添加tailrec关键字，现在将NODE_COUNT值设为30000（这里不打印toString了）

fun main() 
    val NODE_COUNT = 30000

    val rootNode:ListNode? = ListNode(0)
    var p = rootNode
    for (i in 1..NODE_COUNT)
        p?.next = ListNode(i)
        p = p?.next
    

    println(findListNode(rootNode,NODE_COUNT-2)?.value)

运行，发现StackOverflowError错误

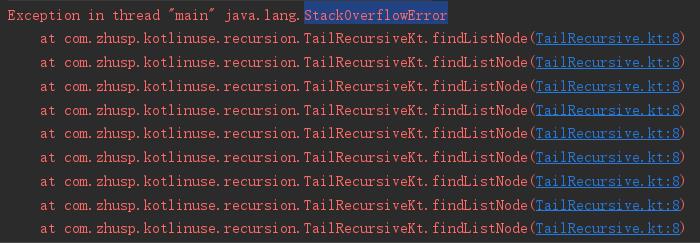
现在给尾递归函数添加tailrec关键字

tailrec fun findListNode(head:ListNode?,value:Int):ListNode?
    head?:return null
    if (head.value == value) return head
    return findListNode(head.next,value)

再次运行，不再报错

这就是尾递归优化，给尾递归函数添加tailrec关键字后编译器自动给函数优化了
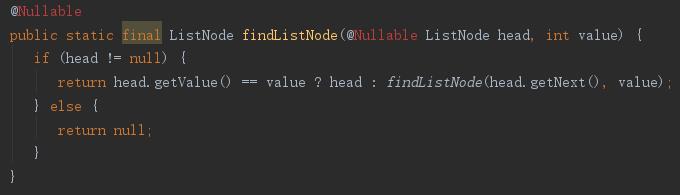
那，究竟优化了什么呢，先看下优化前（也就是不添加tailrec时）findListNode对应的java代码

在看下优化后（即添加tailrec后）findListNode对应的java代码

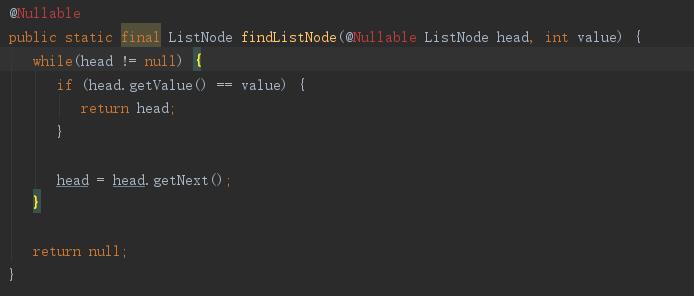
我们发现，没有优化的findListNode对应的java代码依然是递归函数，优化后（即添加了tailrec关键字）的findListNode方法对应的java代码已经不再是递归函数，而是通过循环来实现功能，这样就不会再出现stackoverflowerror了，这样我们就在kotlin中既实现了递归函数代码简洁的优势，又规避了在java中使用递归函数容易出出现的问题