Lesson 10.1 超参数优化与枚举网格的理论极限和随机网格搜索 RandomSearchCV

Posted 2023-04-08 虚心求知的熊

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Lesson 10.1 超参数优化与枚举网格的理论极限和随机网格搜索 RandomSearchCV相关的知识，希望对你有一定的参考价值。

文章目录

一、超参数优化与枚举网格的理论极限
二、随机网格搜索 RandomizedSearchCV

首先，导入我们需要的库。

import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import seaborn as sns
import time
import re, pip, conda

一、超参数优化与枚举网格的理论极限

1. 超参数优化 HPO（HyperParameter Optimization）

每一个机器学习算法都会有超参数，而超参数的设置很大程度上影响了算法实际的使用效果，因此调参是机器学习算法工程师最为基础和重要的任务。
现代机器学习与深度学习算法的超参数量众多，不仅实现方法异常灵活、算法性能也受到更多的参数的复合影响，因此当人工智能浪潮来临时，可以自动选择超参数的超参数优化 HPO 领域也迎来了新一轮爆发。
在算法的世界中，我们渴望一切流程最终都走向完美自动化，专门研究机器学习自动化的学科被称为 AutoML，而超参数自动优化是 AutoML 中最成熟、最深入、也是最知名的方向。
理论上来说，当算力与数据足够时，HPO 的性能一定是超过人类的。HPO 能够降低人为工作量，并且 HPO 得出的结果比认为搜索的复现可能性更高，所以 HPO 可以极大程度提升科学研究的复现性和公平性。当代超参数优化算法主要可以分为：
（1）基于网格的各类搜索（Grid）。
（2）基于贝叶斯优化的各类优化算法（Baysian）。
（3）基于梯度的各类优化（Gradient-based）。
（4）基于种群的各类优化（进化算法，遗传算法等）。
其中，各类网格搜索方法与基于贝叶斯的优化方法是最为盛行的，贝叶斯优化方法甚至可以被称为是当代超参数优化中的 SOTA 模型。这些模型对于复杂集成算法的调整有极大的作用与意义。

2. 网格搜索的理论极限与缺点

在所有超参数优化的算法当中，枚举网格搜索是最为基础和经典的方法。在搜索开始之前，我们需要人工将每个超参数的备选值一一列出，多个不同超参数的不同取值之间排列组合，最终将组成一个参数空间（parameter space）。
枚举网格搜索算法会将这个参数空间当中所有的参数组合带入模型进行训练，最终选出泛化能力最强的组合作为模型的最终超参数。
对网格搜索而言，如果参数空间中的某一个点指向了损失函数真正的最小值，那枚举网格搜索时一定能够捕捉到该最小值以及对应的参数（相对的，假如参数空间中没有任意一点指向损失函数真正的最小值，那网格搜索就一定无法找到最小值对应的参数组合）。
参数空间越大、越密，参数空间中的组合刚好覆盖损失函数最小值点的可能性就会越大。这是说，极端情况下，当参数空间穷尽了所有可能的取值时，网格搜索一定能够找到损失函数的最小值所对应的最优参数组合，且该参数组合的泛化能力一定是强于人工调参的。
但是，参数空间越大，网格搜索所需的算力和时间也会越大，当参数维度上升时，网格搜索所需的计算量更是程指数级上升的。以随机森林为例：
只有 1 个参数 n_estimators，备选范围是 [50,100,150,200,250,300]，需要建模 6 次。
当我们增加参数 max_depth，且备选范围是 [2,3,4,5,6]，需要建模 30 次。
当我们增加参数 min_sample_split，且备选范围为 [2,3,4,5]，需要建模 120 次。
同时，参数优化的目标是找出令模型泛化能力最强的组合，因此需要交叉验证来体现模型的泛化能力，假设交叉验证次数为 5，则三个参数就需要建模 600 次。
在面对超参数众多、且超参数取值可能无限的人工神经网络、融合模型、集成模型时，伴随着数据和模型的复杂度提升，网格搜索所需要的时间会急剧增加，完成一次枚举网格搜索可能需要耗费几天几夜。

3. 建立 benchmark：随机森林中枚举网格搜索的结果

from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate, KFold, GridSearchCV

data = pd.read_csv(r"D:\\Pythonwork\\2021ML\\PART 2 Ensembles\\datasets\\House Price\\train_encode.csv",index_col=0)

X = data.iloc[:,:-1]
y = data.iloc[:,-1]

X.shape
#(1460, 80)

X.head()

y.describe() #RMSE

#参数空间
param_grid_simple = "criterion": ["squared_error","poisson"]
                     , 'n_estimators': [*range(20,100,5)]
                     , 'max_depth': [*range(10,25,2)]
                     , "max_features": ["log2","sqrt",16,32,64,"auto"]
                     , "min_impurity_decrease": [*np.arange(0,5,10)]
                    

#参数空间大小计算
2 * len([*range(20,100,5)]) * len([*range(10,25,2)]) * len(["log2","sqrt",16,32,64,"auto"]) * len([*np.arange(0,5,10)])
#1536

#直接使用循环计算
no_option = 1
for i in param_grid_simple:
    no_option *= len(param_grid_simple[i])

no_option
#1536

#模型，交叉验证，网格搜索
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
search = GridSearchCV(estimator=reg
                     ,param_grid=param_grid_simple
                     ,scoring = "neg_mean_squared_error"
                     ,verbose = True
                     ,cv = cv
                     ,n_jobs=-1)

#=====【TIME WARNING: 7mins】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
Fitting 5 folds for each of 1536 candidates, totalling 7680 fits
#381.6039867401123

381.6039/60
#6.3600650000000005

search.best_estimator_
#RandomForestRegressor(max_depth=23, max_features=16, min_impurity_decrease=0,
#                      n_estimators=85, n_jobs=-1, random_state=1412,
#                      verbose=True)

abs(search.best_score_)**0.5
#29179.698261599166

#按最优参数重建模型，查看效果
ad_reg = RFR(n_estimators=85, max_depth=23, max_features=16, random_state=1412)

cv = KFold(n_splits=5,shuffle=True,random_state=1412)
result_post_adjusted = cross_validate(ad_reg,X,y,cv=cv,scoring="neg_mean_squared_error"
                          ,return_train_score=True
                          ,verbose=True

                          ,n_jobs=-1)

def RMSE(cvresult,key):
    return (abs(cvresult[key])**0.5).mean()

RMSE(result_post_adjusted,"train_score")
#11000.81099038192

RMSE(result_post_adjusted,"test_score")
#28572.070208366855

HPO方法	默认参数	网格搜索
搜索空间/全域空间	-	1536/1536
运行时间（分钟）	-	6.36
搜索最优（RMSE）	30571.266	29179.698
重建最优（RMSE）	-	28572.070

#打包成函数供后续使用
#评估指标RMSE
def RMSE(cvresult,key):
    return (abs(cvresult[key])**0.5).mean()

#计算参数空间大小
def count_space(param):
    no_option = 1
    for i in param_grid_simple:
        no_option *= len(param_grid_simple[i])
    print(no_option)
    
#在最优参数上进行重新建模验证结果
def rebuild_on_best_param(ad_reg):
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    result_post_adjusted = cross_validate(ad_reg,X,y,cv=cv,scoring="neg_mean_squared_error"
                                          ,return_train_score=True
                                          ,verbose=True
                                          ,n_jobs=-1)
    print("训练RMSE::.3f".format(RMSE(result_post_adjusted,"train_score")))
    print("测试RMSE::.3f".format(RMSE(result_post_adjusted,"test_score")))

二、随机网格搜索 RandomizedSearchCV

1. 基本原理

在讲解网格搜索时我们提到，伴随着数据和模型的复杂度提升，网格搜索所需要的时间急剧增加。以随机森林算法为例，如果使用过万的数据，搜索时间则会立刻上升好几个小时。因此，我们急需寻找到一种更加高效的超参数搜索方法。
首先，当所使用的算法确定时，决定枚举网格搜索运算速度的因子一共有两个：
（1）参数空间的大小：参数空间越大，需要建模的次数越多。
（2）数据量的大小：数据量越大，每次建模时需要的算力和时间越多。
因此，sklearn 中的网格搜索优化方法主要包括两类，其一是调整搜索空间，其二是调整每次训练的数据。其中，调整参数空间的具体方法，是放弃原本的搜索中必须使用的全域超参数空间，改为挑选出部分参数组合，构造超参数子空间，并只在子空间中进行搜索。
以下图的二维空间为例，在这个 n_estimators 与 max_depth 共同组成的参数空间中，n_estimators 的取值假设为 [50,100,150,200,250,300]，max_depth 的取值假设为 [2,3,4,5,6]，则枚举网格搜索必须对 30 种参数组合都进行搜索。
当我们调整搜索空间，我们可以只抽样出橙色的参数组合作为子空间，并只对橙色参数组合进行搜索。

fig, [ax1, ax2] = plt.subplots(1,2,dpi=300)
n_e_list = [*range(50,350,50)]
m_d_list = [*range(2,7)]
comb = pd.DataFrame([(n_estimators, max_depth) for n_estimators in n_e_list for max_depth in m_d_list])

ax1.scatter(comb.iloc[:,0],comb.iloc[:,1],cmap="Blues")
ax1.set_xticks([*range(50,350,50)])
ax1.set_yticks([*range(2,7)])
ax1.set_xlabel("n_estimators")
ax1.set_ylabel("max_depth")
ax1.set_title("GridSearch")

ax2.scatter(comb.iloc[:,0],comb.iloc[:,1],cmap="Blues")
ax2.scatter([50,250,200,200,300,100,150,150],[4,2,6,3,2,3,2,5],cmap="red",s=20,linewidths=5)
ax2.set_xticks([*range(50,350,50)])
ax2.set_yticks([*range(2,7)])
ax2.set_xlabel("n_estimators")
ax2.set_ylabel("max_depth")
ax2.set_title("RandomSearch");

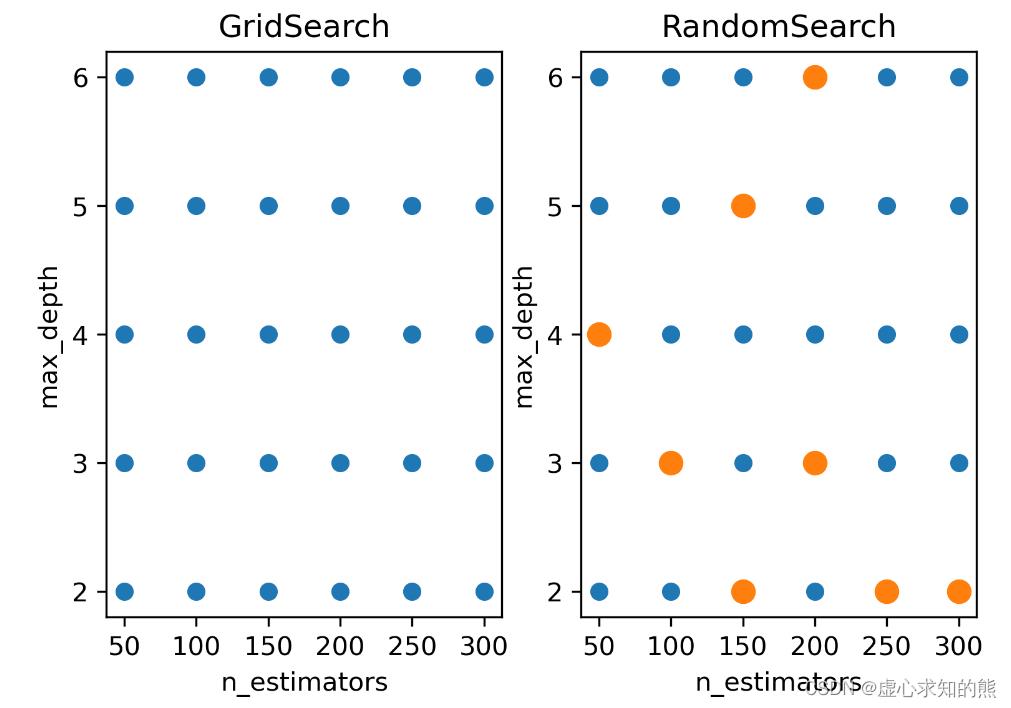
在 sklearn 中，随机抽取参数子空间并在子空间中进行搜索的方法叫做随机网格搜索 RandomizedSearchCV。
由于搜索空间的缩小，需要枚举和对比的参数组的数量也对应减少，整体搜索耗时也将随之减少，因此：
当设置相同的全域空间时，随机搜索的运算速度比枚举网格搜索快很多。
当设置相同的训练次数时，随机搜索可以覆盖的空间比枚举网格搜索大很多。
同时，绝妙的是，随机网格搜索得出的最小损失与枚举网格搜索得出的最小损失很接近。
可以说，是提升了运算速度，又没有过多地伤害搜索的精度。
不过，需要注意的是，随机网格搜索在实际运行时，并不是先抽样出子空间，再对子空间进行搜索，而是仿佛循环迭代一般，在这一次迭代中随机抽取 1 组参数进行建模，下一次迭代再随机抽取 1 组参数进行建模，由于这种随机抽样是不放回的，因此不会出现两次抽中同一组参数的问题。
我们可以控制随机网格搜索的迭代次数，来控制整体被抽出的参数子空间的大小，这种做法往往被称为赋予随机网格搜索固定的计算量，当全部计算量被消耗完毕之后，随机网格搜索就停止。

2. 随机网格搜索的实现

from sklearn.model_selection import RandomizedSearchCV

其函数语法模板如下：

class sklearn.model_selection.RandomizedSearchCV(estimator, param_distributions, *, n_iter=10, scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', random_state=None, error_score=nan, return_train_score=False)

全部参数解读如下，其中加粗的是随机网格搜索独有的参数：

Name	Description
estimator	调参对象，某评估器
param_distributions	全域参数空间，可以是字典或者字典构成的列表
n_iter	迭代次数，迭代次数越多，抽取的子参数空间越大
scoring	评估指标，支持同时输出多个参数
n_jobs	设置工作时参与计算的线程数
refit	挑选评估指标和最佳参数，在完整数据集上进行训练
cv	交叉验证的折数
verbose	输出工作日志形式
pre_dispatch	多任务并行时任务划分数量
random_state	随机数种子
error_score	当网格搜索报错时返回结果，选择’raise’时将直接报错并中断训练过程，其他情况会显示警告信息后继续完成训练
return_train_score	在交叉验证中是否显示训练集中参数得分

我们依然借用之前在网格搜索上见过的 X 和 y，以及随机森林回归器，来实现随机网格搜索：

X.shape
#(1460, 80)

X.head()

y.describe()

3. 相同的全域参数空间

我们先创造参数空间，也就是和使用与网格搜索时完全一致的空间，以便于进行对比操作。

param_grid_simple = "criterion": ["squared_error","poisson"]
                     , 'n_estimators': [*range(20,100,5)]
                     , 'max_depth': [*range(10,25,2)]
                     , "max_features": ["log2","sqrt",16,32,64,"auto"]
                     , "min_impurity_decrease": [*np.arange(0,5,10)]

然后建立回归器。进行交叉验证。

reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)

计算全域参数空间大小，这是我们能够抽样的最大值。

count_space(param_grid_simple)
#1536

进行定义随机搜索。

search = RandomizedSearchCV(estimator=reg
                            ,param_distributions=param_grid_simple
                            ,n_iter = 800 #子空间的大小是全域空间的一半左右
                            ,scoring = "neg_mean_squared_error"
                            ,verbose = True
                            ,cv = cv
                            ,random_state=1412
                            ,n_jobs=-1
                           )

训练随机搜索评估器。

#=====【TIME WARNING: 5~10min】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
#Fitting 5 folds for each of 800 candidates, totalling 4000 fits
#170.16785073280334

170.1678/60
#2.83613

查看模型结果。

search.best_estimator_
#RandomForestRegressor(max_depth=24, max_features=16, min_impurity_decrease=0,
#                      n_estimators=85, n_jobs=-1, random_state=1412,
#                      verbose=True)

abs(search.best_score_)**0.5
#29251.284326350575

根据最优参数重建模型。

ad_reg = RFR(max_depth=24, max_features=16, min_impurity_decrease=0,
                      n_estimators=85, n_jobs=-1, random_state=1412,
                      verbose=True)
rebuild_on_best_param(ad_reg)
#训练RMSE:11031.299
#测试RMSE:28639.969

HPO方法	默认参数	网格搜索	随机搜索
搜索空间/全域空间	-	1536/1536	800/1536
运行时间（分钟）	-	6.36	2.83(↓)
搜索最优（RMSE）	30571.266	29179.698	29251.284
重建最优（RMSE）	-	28572.070	28639.969(↑)

很明显，在相同参数空间、相同模型的情况下，随机网格搜索的运算速度是普通网格搜索的一半，当然，这与子空间是全域空间的一半有很大的联系。
由于随机搜索只是降低搜索的次数，并非影响搜索过程本身，因此其运行时间基本就等于n_iter/全域空间组合数 * 网格搜索的运行时间。

4. 随机网格搜索的理论极限

在机器学习算法当中，有非常多通过随机来提升运算速度（比如 Kmeans，随机挑选样本构建簇心，小批量随机梯度下降，通过随机来减少每次迭代需要的样本）、或通过随机来提升模型效果的操作（比如随机森林，比如极度随机树）。
两种随机背后的原理完全不同，而随机网格搜索属于前者，这一类机器学习方法总是伴随着“从某个全数据集/全域中进行抽样”的操作，而这种操作能够有效的根本原因在于：
（1）抽样出的子空间可以一定程度上反馈出全域空间的分布，且子空间相对越大（含有的参数组合数越多），子空间的分布越接近全域空间的分布。
（2）当全域空间本身足够密集时，很小的子空间也能获得与全域空间相似的分布。
（3）如果全域空间包括了理论上的损失函数最小值，那一个与全域空间分布高度相似的子空间很可能也包括损失函数的最小值，或包括非常接近最小值的一系列次小值。
我们可以通过绘制图像来直观地呈现这些事实。许多在数学上比较抽象的概念都可以被可视化。在这里，我们借助 matplotlib 工具库 mplot3d 中的一组默认数据。

from mpl_toolkits.mplot3d import axes3d

p1, p2, MSE = axes3d.get_test_data(0.05)

其中，get_test_data 巨头自动获取数据的功能，可以自动生成复合某一分布的数据。我们现在假设这一组数据中有两个参数，p1 与 p2，两个参数组成的参数组合对应着损失函数值 MSE。
参数 0.05 是指参数空间中，点与点之间的距离。因此该数字越小，取出来的样本越多。

len(p1) #参数1的取值有120个
#120

len(p2) #参数2的取值也有120个
#120

那么，现在参数空间当中一共有 120*120=14400 种组合，所以参数空间中一共有 14400 个点。

MSE.shape #损失函数值，总共14400个点
#(120, 120)

随后，我们绘制 P1 与 P2 的参数空间，这是一个呈现出 14400 个点的密集空间。

plt.figure(dpi=300)
plt.scatter(p1,p2,s=0.2)
plt.xticks(fontsize=9)
plt.yticks(fontsize=9)

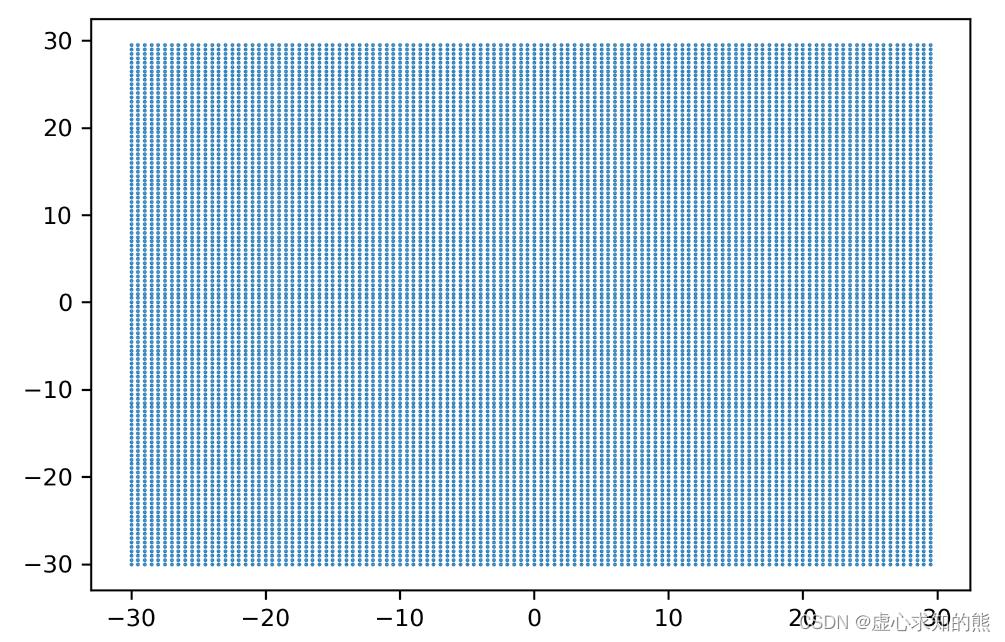
参数与损失共同构建的函数。

p1, p2, MSE = axes3d.get_test_data(0.05)
plt.figure(dpi=300)
ax = plt.axes(projection="3d")
ax.plot_wireframe(p1,p2,MSE,rstride=2,cstride=2,linewidth=0.5)
ax.view_init(2, -15)
ax.zaxis.set_tick_params(labelsize=7)
ax.xaxis.set_tick_params(labelsize=7)
ax.yaxis.set_tick_params(labelsize=7)

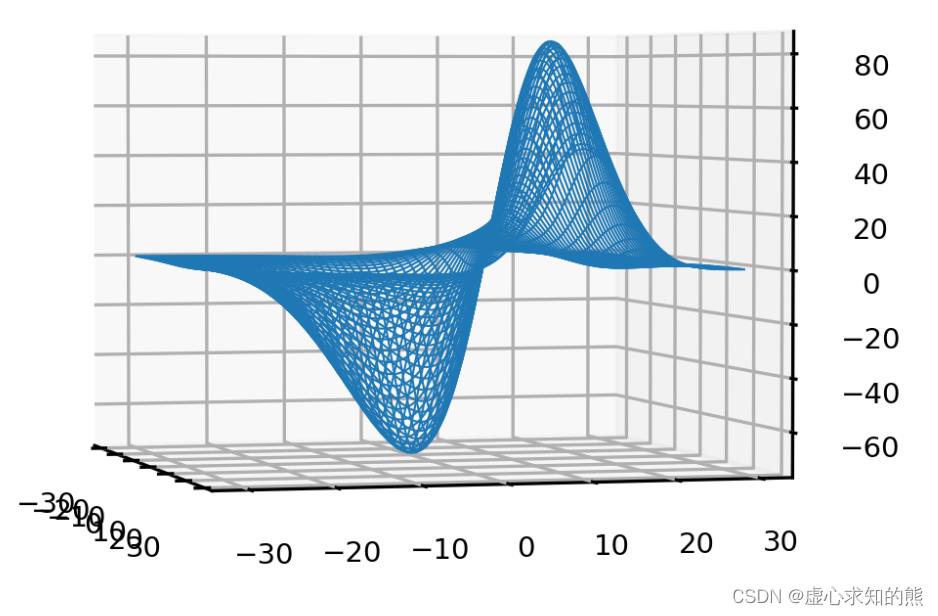
np.min(MSE) #整个参数空间中，可获得的MSE最小值是-73.39
#-73.39620971601681

现在，我们从该空间上抽取子空间。

MSE.shape
#(120, 120)

我们从空间中抽取 n 个组合，n 越大子空间越大。现在总共有 14400 个组合，对被抽中的点来说，损失函数的值就是 MSE，对没有抽中的点来说，损失函数值是空值。
因此，我们只需要找出没有抽中的点，并让它的损失函数值 MSE 为空就可以了。从 0~14400 中生成（14400-n）个随机数，形成没有被抽到子空间中的点的索引。

n = 100
unsampled = np.random.randint(0,14400,14400-n)
p1, p2, MSE = axes3d.get_test_data(0.05)

拉平 MSE，并将所有没抽中的点的损失函数变为空值。

MSE = MSE.ravel()
MSE[unsampled] = np.nan
MSE = MSE.reshape((120,120))

设置完毕空值后，记得把 MSE 恢复成原来的结构，否则绘图报错。

#参数与损失共同构建的函数
plt.figure(dpi=300)
ax = plt.axes(projection=Lesson 9.3 集成算法的参数空间与网格优化和使用网格搜索在随机森林上进行调参



 文章目录
 一、集成算法的参数空间与网格优化
1. 学习曲线
2. 决策树对象 Tree
  
二、使用网格搜索在随机森林上进行调参
1. 建立 benchmark
2. 创建参数空间
3. 实例化用于搜索的评估器、交叉验证评估器与网格搜索评估器
4. 训练网格搜索评估器
5. 查看结果
 

 
在开始学习之前，先导入我们需要的库。 
import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import seaborn as sns
import re, pip, conda
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.tree import DecisionTreeRegressor as DTR
from sklearn.model_selection import cross_validate, KFold
 
一、集成算法的参数空间与网格优化 
如随机森林中所展示的，集成算法的超参数种类繁多、取值丰富，且参数之间会相互影响、共同作用于算法的最终结果，因此集成算法的调参是一个难度很高的过程。
在超参数优化还未盛行的时候，随机森林的调参是基于方差-偏差理论（variance-bias trade-off）和学习曲线完成的，而现在我们可以依赖于网格搜索来完成自动优化。在对任意算法进行网格搜索时，我们需要明确两个基本事实：
（1） 参数对算法结果的影响力大小。
（2） 用于进行搜索的参数空间。
对随机森林来说，我们可以大致如下排列各个参数对算法的影响： 
影响力 参数
⭐⭐⭐⭐⭐
几乎总是具有巨大影响力 n_estimators（整体学习能力）
max_depth（粗剪枝）
max_features（随机性）
⭐⭐⭐⭐
大部分时候具有影响力 max_samples（随机性）
class_weight（样本均衡）
⭐⭐
可能有大影响力
大部分时候影响力不明显 min_samples_split（精剪枝）
min_impurity_decrease（精剪枝）
max_leaf_nodes（精剪枝）
criterion（分枝敏感度）
⭐
当数据量足够大时，几乎无影响 random_state
ccp_alpha（结构风险）
随机森林在剪枝方面的空间总是很大的，因为默认参数下树的结构基本没有被影响（也就是几乎没有剪枝），因此当随机森林过拟合的时候，我们可以尝试粗、精、随机等各种方式来影响随机森林。通常在网格搜索当中，我们会考虑所有有巨大影响力的参数、以及 1、2 个影响力不明显的参数。
虽然随机森林调参的空间较大，大部分人在调参过程中依然难以突破，因为树的集成模型的参数空间非常难以确定。当没有数据支撑时，人们很难通过感觉或经验来找到正确的参数范围。
举例来说，我们也很难直接判断究竟多少棵树对于当前的模型最有效，同时，我们也很难判断不剪枝时一棵决策树究竟有多深、有多少叶子、或者一片叶子上究竟有多少个样本，更不要谈凭经验判断树模型整体的不纯度情况了。
可以说，当森林建好之后，我们简直是对森林一无所知。对于网格搜索来说，新增一个潜在的参数可选值，计算量就会指数级增长，因此找到有效的参数空间非常重要。此时我们就要引入两个工具来帮助我们：
（1） 学习曲线。
（2） 决策树对象 Tree 的属性。 
1. 学习曲线 
学习曲线是以参数的不同取值为横坐标，模型的结果为纵坐标的曲线。当模型的参数较少、且参数之间的相互作用较小时，我们可以直接使用学习曲线进行调参。
但对于集成算法来说，学习曲线更多是我们探索参数与模型关系的关键手段。许多参数对模型的影响是确定且单调的，例如 n_estimators，树越多模型的学习能力越强，再比如 ccp_alpha，该参数值越大模型抗过拟合能力越强，因此我们可能通过学习曲线找到这些参数对模型影响的极限。
我们会围绕这些极限点来构筑我们的参数空间。
我们先来看看 n_estimators 的学习曲线： 
#参数潜在取值，由于现在我们只调整一个参数，因此参数的范围可以取大一些、取值也可以更密集
Option = [1,*range(5,101,5)]

#生成保存模型结果的arrays
trainRMSE = np.array([])
testRMSE = np.array([])
trainSTD = np.array([])
testSTD = np.array([])

#在参数取值中进行循环
for n_estimators in Option:
    
    #按照当下的参数，实例化模型
    reg_f = RFR(n_estimators=n_estimators,random_state=1412)
    
    #实例化交叉验证方式，输出交叉验证结果
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    result_f = cross_validate(reg_f,X,y,cv=cv,scoring="neg_mean_squared_error"
                              ,return_train_score=True
                              ,n_jobs=-1)
    
    #根据输出的MSE进行RMSE计算
    train = abs(result_f["train_score"])**0.5
    test = abs(result_f["test_score"])**0.5
    
    #将本次交叉验证中RMSE的均值、标准差添加到arrays中进行保存
    trainRMSE = np.append(trainRMSE,train.mean()) #效果越好
    testRMSE = np.append(testRMSE,test.mean())
    trainSTD = np.append(trainSTD,train.std()) #模型越稳定
    testSTD = np.append(testSTD,test.std())

def plotCVresult(Option,trainRMSE,testRMSE,trainSTD,testSTD):
    #一次交叉验证下，RMSE的均值与std的绘图
    xaxis = Option
    plt.figure(figsize=(8,6),dpi=80)

    #RMSE
    plt.plot(xaxis,trainRMSE,color="k",label = "RandomForestTrain")
    plt.plot(xaxis,testRMSE,color="red",label = "RandomForestTest")

    #标准差 - 围绕在RMSE旁形成一个区间
    plt.plot(xaxis,trainRMSE+trainSTD,color="k",linestyle="dotted")
    plt.plot(xaxis,trainRMSE-trainSTD,color="k",linestyle="dotted")
    plt.plot(xaxis,testRMSE+testSTD,color="red",linestyle="dotted")
    plt.plot(xaxis,testRMSE-testSTD,color="red",linestyle="dotted")
    plt.xticks([*xaxis])
    plt.legend(loc=1)
    plt.show()

plotCVresult(Option,trainRMSE,testRMSE,trainSTD,testSTD)
 
 
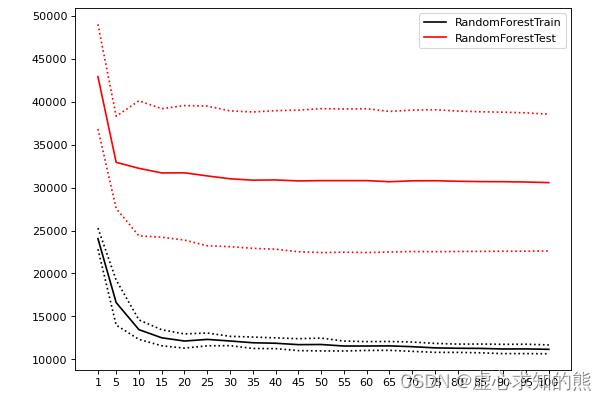
当绘制学习曲线时，我们可以很容易找到泛化误差开始上升、或转变为平稳趋势的转折点。因此我们可以选择转折点或转折点附近的 n_estimators 取值，例如 20。然而，n_estimators 会受到其他参数的影响，例如：
（1） 单棵决策树的结构更简单时（依赖剪枝时），可能需要更多的树。
（2） 单棵决策树训练的数据更简单时（依赖随机性时），可能需要更多的树。
因此 n_estimators 的参数空间可以被确定为 range(20,100,5)，如果你比较保守，甚至可以确认为是 range(15,25,5)。 
2. 决策树对象 Tree 
在 sklearn 中，树模型是单独的一类对象，每个树模型背后都有一套完整的属性供我们调用，包括树的结构、树的规模等众多细节。在之前的课程中，我们曾经使用过树模型的绘图功能 plot_tree，除此之外树还有许多有用的属性。随机森林是树组成的算法，因此也可以调用这些属性。我们来举例说明： 
reg_f = RFR(n_estimators=10,random_state=1412)
reg_f = reg_f.fit(X,y) #训练一个随机森林
 
属性 .estimators_ 可以查看森林中所有的树。 
reg_f.estimators_ #一片随机森林中所有的树
#[DecisionTreeRegressor(max_features='auto', random_state=1630984966),
# DecisionTreeRegressor(max_features='auto', random_state=472863509),
# DecisionTreeRegressor(max_features='auto', random_state=1082704530),
# DecisionTreeRegressor(max_features='auto', random_state=1930362544),
# DecisionTreeRegressor(max_features='auto', random_state=273973624),
# DecisionTreeRegressor(max_features='auto', random_state=21991934),
# DecisionTreeRegressor(max_features='auto', random_state=1886585710),
# DecisionTreeRegressor(max_features='auto', random_state=63725675),
# DecisionTreeRegressor(max_features='auto', random_state=1374343434),
# DecisionTreeRegressor(max_features='auto', random_state=1078007175)]

#可以用索引单独提取一棵树
reg_f.estimators_[0]
#DecisionTreeRegressor(max_features='auto', random_state=1630984966)

#调用这棵树的底层结构
reg_f.estimators_[0].tree_
#<sklearn.tree._tree.Tree at 0x1c070d8e340>
 
属性 .max_depth 可以查看当前树的实际深度。 
reg_f.estimators_[0].tree_.max_depth #max_depth=None
#19

#对森林中所有树查看实际深度
for t in reg_f.estimators_:
    print(t.tree_.max_depth)
#19
#25
#27
#20
#23
#22
#22
#20
#22
#24

#如果树的数量较多，也可以查看平均或分布
reg_f = RFR(n_estimators=100,random_state=1412)
reg_f = reg_f.fit(X,y) #训练一个随机森林
d = pd.Series([],dtype="int64")
for idx,t in enumerate(reg_f.estimators_):
    d[idx] = t.tree_.max_depth

d.mean()
#22.25

d.describe()
#count    100.000000
#mean      22.250000
#std        1.955954
#min       19.000000
#25%       21.000000
#50%       22.000000
#75%       23.000000
#max       30.000000
#dtype: float64
 
假设现在你的随机森林过拟合，max_depth 的最大深度范围设置在 [15,25] 之间就会比较有效，如果我们希望激烈地剪枝，则可以设置在 [10,15] 之间。
相似的，我们也可以调用其他属性来辅助我们调参： 
参数 参数含义 对应属性 属性含义
n_estimators 树的数量 reg.estimators_ 森林中所有树对象
max_depth 允许的最大深度 .tree_.max_depth 0号树实际的深度
max_leaf_nodes 允许的最大
叶子节点量 .tree_.node_count 0号树实际的总节点量
min_sample_split 分枝所需最小
样本量 .tree_.n_node_samples 0号树每片叶子上实际的样本量
min_weight_fraction_leaf 分枝所需最小
样本权重 tree_.weighted_n_node_samples 0号树每片叶子上实际的样本权重
min_impurity_decrease 分枝所需最小
不纯度下降量 .tree_.impurity
.tree_.threshold 0号树每片叶子上的实际不纯度
0号树每个节点分枝后不纯度下降量
#一棵树上的总叶子量
#reg_f.estimators_[0].tree_.node_count
1807

#所有树上的总叶子量
for t in reg_f.estimators_:
    print(t.tree_.node_count)
#1807
#1777
#1763
#1821
#1777
#1781
#1811
#1771
#1753
#1779
 
根据经验，当决策树不减枝且在训练集上的预测结果不错时，一棵树上的叶子量常常与样本量相当或比样本量更多，算法结果越糟糕，叶子量越少，如果 RMSE 很高或者 R2 很低，则可以考虑使用样本量的一半或 3/4 作为不减枝时的叶子量的参考。 
#每个节点上的不纯度下降量，为-2则表示该节点是叶子节点
reg_f.estimators_[0].tree_.threshold.tolist()[:20]
#[6.5,
# 5.5,
# 327.0,
# 214.0,
# 0.5,
# 1.0,
# 104.0,
# 0.5,
# -2.0,
# -2.0,
# -2.0,
# 105.5,
# 28.5,
# 0.5,
# 1.5,
# -2.0,
# -2.0,
# 11.0,
# 1212.5,
# 2.5]

#你怎么知道min_impurity_decrease的范围设置多少会剪掉多少叶子？
pd.Series(reg_f.estimators_[0].tree_.threshold).value_counts().sort_index()
#-2.0       904
# 0.5        43
# 1.0        32
# 1.5        56
# 2.0        32
#          ... 
# 1118.5      1
# 1162.5      1
# 1212.5      2
# 1254.5      1
# 1335.5      1
#Length: 413, dtype: int64

pd.set_option("display.max_rows",None)
np.cumsum(pd.Series(reg_f.estimators_[0].tree_.threshold).value_counts().sort_index()[1:])
 
从这棵树反馈的结果来看，min_impurity_decrease 在现在的数据集上至少要设置到 [2,10] 的范围才可能对模型有较大的影响。 
#min_sample_split的范围要如何设置才会剪掉很多叶子？
np.bincount(reg_f.estimators_[0].tree_.n_node_samples.tolist())[:10]
#array([  0, 879, 321, 154,  86,  52,  42,  38,  29,  18], dtype=int64)
 
更多属性可以参考： 
from sklearn.tree._tree import Tree

type(Tree)
#type

help(Tree)
 
二、使用网格搜索在随机森林上进行调参 
影响力 参数
⭐⭐⭐⭐⭐
几乎总是具有巨大影响力 n_estimators（整体学习能力）
max_depth（粗剪枝）
max_features（随机性）
⭐⭐⭐⭐
大部分时候具有影响力 max_samples（随机性）
class_weight（样本均衡）
⭐⭐
可能有大影响力
大部分时候影响力不明显 min_samples_split（精剪枝）
min_impurity_decrease（精剪枝）
max_leaf_nodes（精剪枝）
criterion（分枝敏感度）
⭐
当数据量足够大时，几乎无影响 random_state
ccp_alpha（结构风险）
现在模型正处于过拟合的状态，需要抗过拟合，且整体数据量不是非常多，随机抽样的比例不宜减小，因此我们挑选以下五个参数进行搜索：n_estimators，max_depth，max_features，min_impurity_decrease，criterion。 
import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import time #计时模块time
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate, KFold, GridSearchCV

def RMSE(cvresult,key):
    return (abs(cvresult[key])**0.5).mean()

data = pd.read_csv(r"D:\\Pythonwork\\2021ML\\PART 2 Ensembles\\datasets\\House Price\\train_encode.csv",index_col=0)

X = data.iloc[:,:-1]
y = data.iloc[:,-1]

X.shape
#(1460, 80)

X.head()
#Id	住宅类型	住宅区域	街道接触面积(英尺)	住宅面积	街道路面状况	巷子路面状况	住宅形状(大概)	住宅现状	水电气	...	半开放式门廊面积	泳池面积	泳池质量	篱笆质量	其他配置	其他配置的价值	销售月份	销售年份	销售类型	销售状态
#0	0.0	5.0	3.0	36.0	327.0	1.0	0.0	3.0	3.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	1.0	2.0	8.0	4.0
#1	1.0	0.0	3.0	51.0	498.0	1.0	0.0	3.0	3.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	4.0	1.0	8.0	4.0
#2	2.0	5.0	3.0	39.0	702.0	1.0	0.0	0.0	3.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	8.0	2.0	8.0	4.0
#3	3.0	6.0	3.0	31.0	489.0	1.0	0.0	0.0	3.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	1.0	0.0	8.0	0.0
#4	4.0	5.0	3.0	55.0	925.0	1.0	0.0	0.0	3.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	11.0	2.0	8.0	#4.0
#5 rows × 80 columns
 
1. 建立 benchmark 
reg = RFR(random_state=1412)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)

result_pre_adjusted = cross_validate(reg,X,y,cv=cv,scoring="neg_mean_squared_error"
                          ,return_train_score=True
                          ,verbose=True
                          ,n_jobs=-1)
#[Parallel(n_jobs=-1)]: Using backend LokyBackend with 16 concurrent workers.
#[Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:    1.1s finished

RMSE(result_pre_adjusted,"train_score")
#11177.272008319653

RMSE(result_pre_adjusted,"test_score")
#30571.26665524217
 
2. 创建参数空间 
param_grid_simple = "criterion": ["squared_error","poisson"]
                     , 'n_estimators': [*range(20,100,5)]
                     , 'max_depth': [*range(10,25,2)]
                     , "max_features": ["log2","sqrt",16,32,64,"auto"]
                     , "min_impurity_decrease": [*np.arange(0,5,10)]
                    
 
3. 实例化用于搜索的评估器、交叉验证评估器与网格搜索评估器 
#n_jobs=4/8,verbose=True
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
search = GridSearchCV(estimator=reg
                     ,param_grid=param_grid_simple
                     ,scoring = "neg_mean_squared_error"
                     ,verbose = True
                     ,cv = cv
                     ,n_jobs=-1)
 
4. 训练网格搜索评估器 
#=====【TIME WARNING: 7mins】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
#Fitting 5 folds for each of 1536 candidates, totalling 7680 fits
#381.6039867401123
#[Parallel(n_jobs=-1)]: Using backend ThreadingBackend with 16 concurrent workers.
#[Parallel(n_jobs=-1)]: Done  18 tasks      | elapsed:    0.0s
#[Parallel(n_jobs=-1)]: Done  85 out of  85 | elapsed:    0.0s finished
 
5. 查看结果 
search.best_estimator_
#RandomForestRegressor(max_depth=23, max_features=16, min_impurity_decrease=0,
#                      n_estimators=85, n_jobs=-1, random_state=1412,
#                      verbose=True)

abs(search.best_score_)**0.5
#29179.698261599166

ad_reg = RFR(n_estimators=85, max_depth=23, max_features=16, random_state=1412)

cv = KFold(n_splits=5,shuffle=True,random_state=1412)
result_post_adjusted = cross_validate(ad_reg,X,y,cv=cv,scoring="neg_mean_squared_error"
                          ,return_train_score=True
                          ,verbose=True
                          ,n_jobs=-1)
#[Parallel(n_jobs=-1)]: Using backend LokyBackend with 16 concurrent workers.
#[Parallel(n_jobs=-1)]: Done   5 out of   5 | elapsed:    0.2s finished

RMSE(result_post_adjusted,"train_score")
#11000.81099038192

RMSE(result_post_adjusted,"test_score")
#28572.070208366855

#默认值下随机森林的RMSE
xaxis = range(1,6)
plt.figure(figsize=(8,6),dpi=80)
#RMSE
plt.plot(xaxis,abs(result_pre_adjusted["train_score"])**0.5,color="green",label = "RF_pre_ad_Train")
plt.plot(xaxis,abs(result_pre_adjusted["test_score"])**0.5,color="green",linestyle="--",label = "RF_pre_ad_Test")
plt.plot(xaxis,abs(result_post_adjusted["train_score"])**0.5,color="orange",label = "RF_post_ad_Train")
plt.plot(xaxis,abs(result_post_adjusted["test_score"])**0.5,color="orange",linestyle="--",label = "RF_post_ad_Test")
plt.xticks([1,2,3,4,5])
plt.xlabel("CVcounts",fontsize=16)
plt.ylabel("RMSE",fontsize=16)
plt.legend()
plt.show()
 
 
不难发现，网格搜索之后的模型过拟合程度减轻，且在训练集与测试集上的结果都有提高，可以说从根本上提升了模型的基础能力。我们还可以根据网格的结果继续尝试进行其他调整，来进一步降低模型在测试集上的 RMSE。
以上是关于Lesson 10.1 超参数优化与枚举网格的理论极限和随机网格搜索 RandomSearchCV的主要内容，如果未能解决你的问题，请参考以下文章 
 scikit-learn 中的超参数优化（网格搜索）
 有没有办法在 One-Class SVM 上执行网格搜索超参数优化
 Scikit 网格搜索参数（不是超参数）
 使用贝叶斯优化对深度学习结构进行超参数优化
 我应该在 SMOTE 之前还是之后执行网格搜索（用于调整超参数）？
 Python：没有机器学习的网格搜索？

影响力	参数
⭐⭐⭐⭐⭐ 几乎总是具有巨大影响力	n_estimators（整体学习能力） max_depth（粗剪枝） max_features（随机性）
⭐⭐⭐⭐ 大部分时候具有影响力	max_samples（随机性） class_weight（样本均衡）
⭐⭐ 可能有大影响力大部分时候影响力不明显	min_samples_split（精剪枝） min_impurity_decrease（精剪枝） max_leaf_nodes（精剪枝） criterion（分枝敏感度）
⭐ 当数据量足够大时，几乎无影响	random_state ccp_alpha（结构风险）

参数	参数含义	对应属性	属性含义
n_estimators	树的数量	reg.estimators_	森林中所有树对象
max_depth	允许的最大深度	.tree_.max_depth	0号树实际的深度
max_leaf_nodes	允许的最大叶子节点量	.tree_.node_count	0号树实际的总节点量
min_sample_split	分枝所需最小样本量	.tree_.n_node_samples	0号树每片叶子上实际的样本量
min_weight_fraction_leaf	分枝所需最小样本权重	tree_.weighted_n_node_samples	0号树每片叶子上实际的样本权重
min_impurity_decrease	分枝所需最小不纯度下降量	.tree_.impurity .tree_.threshold	0号树每片叶子上的实际不纯度 0号树每个节点分枝后不纯度下降量