Python求解线性方程组

Posted 2023-04-07 微小冷

文章目录

• • solve
  • 带状矩阵
  • 三角矩阵
  • 循环矩阵

scipy.linalg中封装了一系列用于求解矩阵方程的算法，列表如下

函数	方程	备注
solve(a, b)	$ax=b$
solve_banded((l, u), ab, b)	$ax=b$	a为带状矩阵
solveh_banded(ab, b)	$ax=b$	a为厄密正定带状矩阵
solve_circulant(c, b)	$cx=b$	c是循环矩阵
solve_triangular(a, b)	$ax=b$	a是三角阵

solve

solve是一个功能十分强大的函数，可用于求解形如a@x=b之类的问题，其参数如下

solve(a, b, lower=False, overwrite_a=False, overwrite_b=False, check_finite=True, assume_a='gen', transposed=False)

其中assume_a是对矩阵a的特征描述，可选四个字符串

• gen 普通矩阵(generic)
• sym 对称矩阵(symmetric)
• her 厄密特矩阵(hermitian)
• pos 正定矩阵(postive define)

其他参数含义如下

• lower 当assume_a不为gen时可用，若为True，则只计算a的下三角部分，否则只计算上三角部分
• overwrite_a 为True时允许覆盖a的数据
• overwrite_b 为True时允许覆盖b的数据
• check_finite 为True时，检查数据是否全为有限值
• transposed 为True时，计算a.T@x=b

如果允许覆盖a或者b的数据，则可以节省一点内存和运算时间。

import numpy as np
from scipy.linalg import solve
a = np.random.rand(10,10)
x = np.arange(10)
b = a @ x
x1 = solve(a, b)
print(x)
[0 1 2 3 4 5 6 7 8 9]
print(x1)
[-1.28900588e-14  1.00000000e+00  2.00000000e+00  3.00000000e+00
  4.00000000e+00  5.00000000e+00  6.00000000e+00  7.00000000e+00
  8.00000000e+00  9.00000000e+00]

带状矩阵

如果某个方阵的所有非零元素都集中在对角线附近的带状区域，则为带状矩阵。对于带状矩阵$A$，若在$i>j+l$时，$a_{ij}=0$，则$A$的下带宽(lower bandwidth)为$l$；若在$j>i+u$时，$a_{ij}=0$，则$A$的上带宽(upper bandwidth)为$u$。例如下面的$5\times 5$矩阵中，下带宽$l=1$，上带宽$u=2$。

$$\left[\begin{array}{ccccc}\cdot & \cdot & \cdot & 0& 0\\ \cdot & \cdot & \cdot & \cdot & 0\\ 0& \cdot & \cdot & \cdot & \cdot \\ 0& 0& \cdot & \cdot & \cdot \\ 0& 0& 0& \cdot & \cdot \end{array}\right]$$

在scipy.linalg中，solve_banded和solveh_banded均用于$a$为带状矩阵时的求解情况，二者均支持check_finite参数，并且可以选择是否覆盖ab, b等，其他参数列表如下

• solve_banded((l,u), ab, b,)
• solveh_banded(ab, b, lower=False,)

三角矩阵

scipy.linalg另外提供了对三角矩阵的求解方案solve_triangular，亦支持check_finite参数，以及可以选择是否覆盖a, b，其他参数列表如下

• solve_triangular(a, b, trans=0, lower=False, unit_diagonal=False)

其中，unit_diagonal为True时，则假定对角元素为1。

循环矩阵

所谓循环矩阵，其形式为

$$c=\left[\begin{array}{cccccc}{a}_1& a_2& a_3& \cdots & a_n& \\ a_n& a_1& a_3& \cdots & a_{n-1}& \\ a_{n-1}& a_1& a_2& \cdots & a_{n-2}& \\ ⋮& ⋮& ⋮& & ⋮& \\ a_2& a_3& a_4& \cdots & a_1& \end{array}\right]$$

形如$cx=b$这类求解问题，若$c$是循环矩阵，则可通过快速傅里叶变换进行求解：$x=F^{-1}\left[\frac{F[b]}{F[c]}\right]$。在scipy.linalg中，对此进行了封装

scipy.linalg.solve_circulant(c, b, singular='raise', tol=None, caxis=-1, baxis=0, outaxis=0)

除了c,b之外，其他参数含义如下

• singularstr 为"raise"时，则弹出奇异值错误；为lstsq时，返回最小二乘解。
• tol 表示精度
• caxis 当c的维度大于1时，caxis表示循环向量所在轴。
• baxis 当b的维度大于1时，baxis表示计算时代求向量所在轴
• outaxis 若c,b维度大于1，则返回值也是多维的，此时outaxis为x所在轴。

共轭梯度法求解线性方程组python实现

Ax = b

cg方法解方程组，前提是正定对称矩阵哦。

举个例子，求解如下方程组。

 

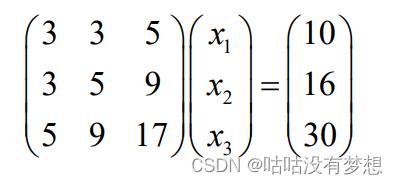
下面是 python代码实现，可推广到任意阶次使用哦，并且迭代n次就会有精确解。

import numpy as np
import pprint

r_list = []
p_list = []
x_list = []
A = np.array([[3, 3,5], [3, 5, 9],[5,9,17]])
b = np.array([[10], [16],[30]])
x_0 = np.array([[0], [0],[0]])
x_list.append(x_0)
r_0 = b - np.dot(A, x_0)
# print(r_0)
r_list.append(r_0)
a_0 = np.vdot(r_0, r_0) / (np.vdot(r_0, np.dot(A, r_0)))  # 乘以用dot，(a,b)用vdot
x_1 = x_0 + np.dot(a_0, r_0)
x_list.append(x_1)

r = r_0
a = a_0
p = r_0
x = x_1
p_list.append(p)

for i in range(2):  # 总次数为n次，这里填n-1
    r = r - np.dot(a, np.dot(A, p))  # r1
    r_list.append(r)
    beita = np.vdot(r_list[-1], r_list[-1]) / np.vdot(r_list[-2], r_list[-2])  # beita 0
    p = r + np.dot(beita, p)  # p1
    p_list.append(p)
    a = np.vdot(r, r) / np.vdot(p, np.dot(A, p))  # a1
    x = x + np.dot(a, p)
    x_list.append(x)
pprint.pprint(x_list)
print()
pprint.pprint(p_list)
print()
pprint.pprint(r_list)

写的多了慢慢的思路清晰多了，继续加油！