逆向-数组
Posted 嘻嘻兮
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了逆向-数组相关的知识，希望对你有一定的参考价值。
对于数组而言，我们需要理解其数组的寻址公式，而其公式又与其内存的分布息息相关，所以当你了解了其内存分布，那么这个公式自然而然也能推出来。
首先数组有如下两点性质
连续性-排列连续
一致性-类型一致因为有其连续的特点，所以其内存模型也就比较好理解，下面我们来看一下如下代码
int arr[5] = 0,1,2,3,4
上面就是其内存模型，对于一致性的特点，可以推定其每个元素占用的空间大小一致，上面的话就是每个元素占4字节（int）
所以我们假设数组开始的首地址为0x10000，那么其各个元素在内存中占的地址是多少呢
arr[0] 0x10000
arr[1] 0x10004
arr[2] 0x10008
arr[3] 0x1000c
arr[4] 0x10010其实很明显，上面就是一个等差数列，所以其一维数组的寻址公式为
ary+sizeof(type)*n
ary[3] -> 0x10000 + 4 * 3 = 0x1000C此时就可以很方便的定位到每一个元素了。下面来看一下对应的一维数组的反汇编
int main(int argc, char* argv[])
int arr[5] = 1,2,3,4,5;
printf("%d",arr[2]);
printf("%d",arr[argc]);
printf("%d",arr[argc%7]);
for(int i=0;i < 5;++i)
printf("%d\\r\\n",arr[i]);
return 0;
对应的反汇编代码
21: int arr[5] = 1,2,3,4,5;
0040D7A8 C7 45 EC 01 00 00 00 mov dword ptr [ebp-14h],1 //说明数组首地址为ebp-0x14
0040D7AF C7 45 F0 02 00 00 00 mov dword ptr [ebp-10h],2
0040D7B6 C7 45 F4 03 00 00 00 mov dword ptr [ebp-0Ch],3
0040D7BD C7 45 F8 04 00 00 00 mov dword ptr [ebp-8],4
0040D7C4 C7 45 FC 05 00 00 00 mov dword ptr [ebp-4],5
22: printf("%d",arr[2]); //arr[2] -> ebp-14 + 4 * 2 = ebp-0c
0040D7CB 8B 45 F4 mov eax,dword ptr [ebp-0Ch]
0040D7CE 50 push eax
0040D7CF 68 1C 20 42 00 push offset string "%d" (0042201c)
0040D7D4 E8 27 39 FF FF call printf (00401100)
0040D7D9 83 C4 08 add esp,8
23: printf("%d",arr[argc]); // arr[argc] -> ebp-14h+argc*4
0040D7DC 8B 4D 08 mov ecx,dword ptr [ebp+8]
0040D7DF 8B 54 8D EC mov edx,dword ptr [ebp+ecx*4-14h] //换个写法 [ebp-14h+ecx*4]
0040D7E3 52 push edx
0040D7E4 68 1C 20 42 00 push offset string "%d" (0042201c)
0040D7E9 E8 12 39 FF FF call printf (00401100)
0040D7EE 83 C4 08 add esp,8
24: printf("%d",arr[argc%7]);
0040D7F1 8B 45 08 mov eax,dword ptr [ebp+8]
0040D7F4 99 cdq
0040D7F5 B9 07 00 00 00 mov ecx,7
0040D7FA F7 F9 idiv eax,ecx //先计算结果此时,结果在edx
0040D7FC 8B 54 95 EC mov edx,dword ptr [ebp+edx*4-14h] //寻址公式和上面相同
0040D800 52 push edx
0040D801 68 1C 20 42 00 push offset string "%d" (0042201c)
0040D806 E8 F5 38 FF FF call printf (00401100)
0040D80B 83 C4 08 add esp,8
25: for(int i=0;i < 5;++i)
0040D80E C7 45 E8 00 00 00 00 mov dword ptr [ebp-18h],0
0040D815 EB 09 jmp main+90h (0040d820)
0040D817 8B 45 E8 mov eax,dword ptr [ebp-18h]
0040D81A 83 C0 01 add eax,1
0040D81D 89 45 E8 mov dword ptr [ebp-18h],eax
0040D820 83 7D E8 05 cmp dword ptr [ebp-18h],5
0040D824 7D 17 jge main+0ADh (0040d83d)
26:
27: printf("%d\\r\\n",arr[i]);
0040D826 8B 4D E8 mov ecx,dword ptr [ebp-18h]
0040D829 8B 54 8D EC mov edx,dword ptr [ebp+ecx*4-14h] //ebp-14h+ecx*4
0040D82D 52 push edx
0040D82E 68 20 20 42 00 push offset string "%d\\r\\n" (00422020)
0040D833 E8 C8 38 FF FF call printf (00401100)
0040D838 83 C4 08 add esp,8
28: 具体的注释都写在里面了，其实最主要的就是套用数组的寻址公式。对于release版下其寻址表现形式差不多，要说区别的话可能就是循环最了点优化。
.text:00401005 mov edi, 5
;....
.text:00401069 lea esi, [esp+1Ch+var_14] //数组首地址
.text:0040106D
.text:0040106D loc_40106D: ; CODE XREF: _main+81↓j
.text:0040106D mov eax, [esi]
.text:0040106F push eax
.text:00401070 push offset aD ; "%d\\r\\n"
.text:00401075 call sub_401090
.text:0040107A add esp, 8
.text:0040107D add esi, 4
.text:00401080 dec edi //edi为计数器
.text:00401081 jnz short loc_40106D对应其高级代码还原
int arr[5] = 1,2,3,4,5;
int count = 5;
int *pAddr = arr;
do
printf("%d",*pAddr);
pAddr++;
count--;
while (count != 0);
下面再来看看二维数组，对于二维数组而言，简单点来说就是多个一维数组而言，既然同样也是数组，那么必然也逃不了开始的两点性质。先来看一下下面的代码
int arr[3][5]=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15;我们先来看一下我们人体中大脑中的表现形式，也就是逻辑层面
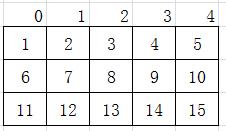当编写二维数组时，我们只需脑海中浮现对应的二维表现形式，那么这个元素值就很好定位了
而在内存中，其表现形式就是把每行都拼接到上一行尾部，所以其本质就是个一维数组
对于二维数组的寻址公式而言，其实我们只需借助上面的逻辑图就可，首先我们可以将二维数组看成多个一位数组，如上面的案例则可看成3个一维数组
3 * int[5]那么此时我们只需要解决如何定位到每个一维数组的首地址即可，由于数组的一致性，所以其每一行占用到固定大小已知，所以，n行指向乘以每行占用的内存即可定位
ary[i][j]
ary + i * sizeof(type) * j //一行有j个,i表示第n行
也可如下表示
ary + sizeof(ary[0]) * i
ary + sizeof(int[j]) * i上面哪种表现形式都可，下面我们来验证一下，如计算ary[2]的首地址
ary[2]
ary + sizeof(int[j]) * i
0x10000 + sizeof(int[5]) * 2
0x10000 + 20 * 2
0x10000 + 0x28
0x10028其实我们可以使用一维数组来验证一下，ary[2]其实相当于就是ary[2][0]的地址，那么对于ary[2][0]，通过上表的内存图可以发现就是ary[10],所以使用一维数组公式进行验证
ary[10]
0x10000 + 10 * sizeof(type)
0x10000 + 10 * 4
0x10000 + 40
0x10028可以发现其结果一致。好了，既然得到其首地址，那么对于ary[2][3]来说，再次使用一维数组的寻址即可，使其寻址到[3]的位置，具体寻址公式就直接看下面吧
(ary + sizeof(ary[0])*i) + sizeof(type) * j
获取首地址 加上 一维数组寻址
ary[2][3] ->
0x10000 + sizeof(int[5]) * 2 + sizeof(int) * 3
0x10028 + 4 * 3
0x10028 + 12
0x10034ary[2]因为上面有同样的公式计算过，所以就直接给出了地址进行下一步的运算。下面再次使用一维数组来验证一下，对于ary[2][3]而言，如果将其看成一维数组，那么应该为ary[13]（2*5+3=13）
ary[13]
0x10000 + 13 * 4
0x10000 + 52
0x10034OK，下面我们再来看一个优化，这里的优化指的是计算优化，对于二维数组的寻址公式其发现需要多次的运算
ary + i * sizeof(type) * j + sizeof(type) * j
//sizeof(type) * j
第一个j表示一行有j个
第二个j表示获取xxx[j]那么既然有公共的部分，自然可以提取优化，最终可以发现其可以减少一个乘法运算
ary[3][5] //为了避免将两个j混乱,这里直接替换常量(真实做法也就是常量)
ary + i * sizeof(type) * j + sizeof(type) * j
ary + sizeof(type) * i * 5 + sizeof(type) * j
ary + sizeof(type) * (5*i+j)好了，这里的优化公式会体现到release版的寻址上，下面我们就来分析一下反汇编，对于二维就直接分析release版吧，毕竟debug就是原原本本的套公式即可
int main(int argc, char* argv[])
int arr[3][5]=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15;
int i,j;
scanf("%d %d",&i,&j);
printf("%d",arr[2][3]);
printf("%d",arr[i][3]);
printf("%d",arr[2][j]);
printf("%d",arr[argc%2][argc/2]);
printf("%d",arr[i][j]);
for(i=0;i < 3;i++)
for(j=0;j < 5;++j)
printf("%d",arr[i][j]);
return 0;
对应的反汇编代码
.text:00401000 ; int __cdecl main(int argc, const char **argv, const char **envp)
.text:00401000 _main proc near ; CODE XREF: start+AF↓p
.text:00401000
.text:00401000 var_44 = dword ptr -44h
.text:00401000 var_40 = dword ptr -40h
.text:00401000 var_3C = dword ptr -3Ch
.text:00401000 var_38 = dword ptr -38h
.text:00401000 var_34 = dword ptr -34h
.text:00401000 var_30 = dword ptr -30h
.text:00401000 var_2C = dword ptr -2Ch
.text:00401000 var_28 = dword ptr -28h
.text:00401000 var_24 = dword ptr -24h
.text:00401000 var_20 = dword ptr -20h
.text:00401000 var_1C = dword ptr -1Ch
.text:00401000 var_18 = dword ptr -18h
.text:00401000 var_14 = dword ptr -14h
.text:00401000 var_10 = dword ptr -10h
.text:00401000 var_C = dword ptr -0Ch
.text:00401000 var_8 = dword ptr -8
.text:00401000 var_4 = dword ptr -4
.text:00401000 argc = dword ptr 4
.text:00401000 argv = dword ptr 8
.text:00401000 envp = dword ptr 0Ch
.text:00401000
.text:00401000 sub esp, 44h
.text:00401003 lea eax, [esp+44h+var_40]
.text:00401007 lea ecx, [esp+44h+var_44]
.text:0040100B push eax
.text:0040100C push ecx
.text:0040100D push offset aDD ; "%d %d"
.text:00401012 mov [esp+50h+var_3C], 1 //首地址
.text:0040101A mov [esp+50h+var_38], 2
.text:00401022 mov [esp+50h+var_34], 3
.text:0040102A mov [esp+50h+var_30], 4
.text:00401032 mov [esp+50h+var_2C], 5
.text:0040103A mov [esp+50h+var_28], 6
.text:00401042 mov [esp+50h+var_24], 7
.text:0040104A mov [esp+50h+var_20], 8
.text:00401052 mov [esp+50h+var_1C], 9
.text:0040105A mov [esp+50h+var_18], 0Ah
.text:00401062 mov [esp+50h+var_14], 0Bh
.text:0040106A mov [esp+50h+var_10], 0Ch
.text:00401072 mov [esp+50h+var_C], 0Dh
.text:0040107A mov [esp+50h+var_8], 0Eh
.text:00401082 mov [esp+50h+var_4], 0Fh
.text:0040108A call _scanf
.text:0040108F push 0Eh //arr[2][3] 直接获取结果
.text:00401091 push offset unk_408030
.text:00401096 call sub_401160
.text:0040109B mov eax, [esp+58h+var_44] //获取i
.text:0040109F lea edx, [eax+eax*4] //edx = i*5 一行有5个元素
.text:004010A2 mov eax, [esp+edx*4+58h+var_30] //var_30相对于var_3C已经往后数了三个,这里使用的是 arr[3] + arr[i] (之前的公式倒一下)
.text:004010A6 push eax //arr[i][3]
.text:004010A7 push offset unk_408030
.text:004010AC call sub_401160
.text:004010B1 mov ecx, [esp+60h+var_40] //获取j
.text:004010B5 mov edx, [esp+ecx*4+60h+var_14] //arr[2]被常量化,相对于一维数组的arr[10]，其值就是[esp+60h+var_14]
.text:004010B9 push edx //arr[2][j]
.text:004010BA push offset unk_408030
.text:004010BF call sub_401160
.text:004010C4 mov eax, [esp+68h+argc]
.text:004010C8 mov ecx, eax
.text:004010CA and ecx, 80000001h
.text:004010D0 jns short loc_4010D7
.text:004010D2 dec ecx
.text:004010D3 or ecx, 0FFFFFFFEh
.text:004010D6 inc ecx
.text:004010D7
.text:004010D7 loc_4010D7: ; CODE XREF: _main+D0↑j
.text:004010D7 cdq
.text:004010D8 sub eax, edx //ecx=argc%2
.text:004010DA lea ecx, [ecx+ecx*4] //优化公式先计算 i*5
.text:004010DD sar eax, 1 //eax = argc/2
.text:004010DF add ecx, eax //i*5+j
.text:004010E1 mov edx, [esp+ecx*4+68h+var_3C] //最后乘以类型大小4
.text:004010E5 push edx
.text:004010E6 push offset unk_408030
.text:004010EB call sub_401160
.text:004010F0 mov eax, [esp+70h+var_44]
.text:004010F4 mov ecx, [esp+70h+var_40]
.text:004010F8 lea edx, [ecx+eax*4] //i*4 + j
.text:004010FB add eax, edx //i*4+j + i = i*5+j
.text:004010FD mov eax, [esp+eax*4+70h+var_3C] //这里也是雷同使用优化公式
.text:00401101 push eax
.text:00401102 push offset unk_408030
.text:00401107 call sub_401160
.text:0040110C add esp, 34h
.text:0040110F xor eax, eax
.text:00401111 mov [esp+44h+var_44], eax
.text:00401115
.text:00401115 loc_401115: ; CODE XREF: _main+14C↓j
.text:00401115 xor ecx, ecx
.text:00401117 mov [esp+44h+var_40], ecx
.text:0040111B
.text:0040111B loc_40111B: ; CODE XREF: _main+142↓j
.text:0040111B lea ecx, [ecx+eax*4]
.text:0040111E add eax, ecx //i*5+j
.text:00401120 mov edx, [esp+eax*4+44h+var_3C] //(i*5+j)*4 + arr
.text:00401124 push edx
.text:00401125 push offset unk_408030
.text:0040112A call sub_401160
.text:0040112F mov ecx, [esp+4Ch+var_40]
.text:00401133 mov eax, [esp+4Ch+var_44]
.text:00401137 add esp, 8
.text:0040113A inc ecx
.text:0040113B cmp ecx, 5 //ecx为j
.text:0040113E mov [esp+44h+var_40], ecx
.text:00401142 jl short loc_40111B
.text:00401144 inc eax
.text:00401145 cmp eax, 3 //eax为i
.text:00401148 mov [esp+44h+var_44], eax
.text:0040114C jl short loc_401115
.text:0040114E xor eax, eax
.text:00401150 add esp, 44h
.text:00401153 retn
.text:00401153 _main endp上面是IDA中粘贴出来的代码，相对来说其代码没有debug那么容易理解，在探究的过程中，建议先使用debug版本看一遍然后再看这个release。
OK，对于多维数组的情况其实和上面都是一致的，这里就大概说说思想，如那三维数组来说，那么我们将其看成多个二维数组即可，或者说没一行就是一个二维，那么因为每行需要占用的空间固定，也就是二维数组的首地址就能确定了，下面就是老套路，调用二维的寻址公式，简单来说对于多维数组的寻址，就是一级一级的降维寻址。
以上是关于逆向-数组的主要内容，如果未能解决你的问题，请参考以下文章