NeRF必读：PixelNeRF

Posted 2023-04-07 Rick0xFFFFFF

NeRF必读：PixelNeRF

前言

NeRF从2020年发展至今，仅仅三年时间，而Follow的工作已呈井喷之势，相信在不久的将来，NeRF会一举重塑三维重建这个业界，甚至重建我们的四维世界（开头先吹一波）。NeRF的发展时间虽短，有几篇工作却在我研究的领域开始呈现万精油趋势：

• PixelNeRF----泛化法宝
• MipNeRF----近远景重建
• NeRF in the wild----光线变换下的背景重建
• Neus----用NeRF重建Surface
• Instant-NGP----多尺度Hash编码实现高效渲染

今天我们就来学习将NeRF泛化的万精油：PixelNeRF。

概述

总体来说PixelNeRF有以下两点比较厉害：

1. 利用稀疏输入构建三维场景表达。
2. 可以基于category泛化三维场景表达（在张三李四上训练，给张王五的照片就能生成王五了，但给张哈士奇不一定能行得通）。

背景

NeRF将空间中的一点$\mathbf{x}\in {\mathbb{R}}^3$在方向$\mathbf{d}$上的观测结果描述为：
$$f(\mathbf{x},\mathbf{d})=(\sigma ,\mathbf{c})$$
通过对函数inference出的$(\sigma ,\mathbf{c})$积分就能渲染出2D图像：
$$\hat{\mathbf{C}}(\mathbf{r})={\int }_{t_n}^{t_f}T(t)\sigma (t)\mathbf{c}(t)dt$$
其中$T(t)=\exp (-{\int }_{t_n}^t\sigma (s)ds)$表示透射率，离镜头越远，透射率越低。
至于Loss就简单了：
$$\mathcal{L}=\sum _{r\in {\mathbb{R}}^3}\Vert \hat{\mathbf{C}}(\mathbf{r})-\mathbf{C}(\mathbf{r}){\Vert }_2^2$$

PixelNeRF指出了NeRF的不足：
NeRF的每个scene都是单独训练的，scene与scene之间并不能共享知识，这对于神经网络这种可以共享先验知识的模型来说是极大的浪费，PixelNeRF的提出希望能弥补这一缺憾。

Image-conditioned NeRF

为了解决NeRF不能共享scenes之间的知识的问题，作者提出了一种Image-conditioned的架构，该架构由两个组件构成：

1. 1个全连接的图像编码器$E$,该编码器给出的图像特征将与原图像逐像素对齐。
2. 1个类NeRF的网络结构，给定空间位置$\mathbf{x}$和相应的编码特征$E(I{)}_x$, NeRF网络输出该点的$(\sigma ,\mathbf{c})$。

具体来说，结合下图与公式，就可以对PixelNeRF有一个非常清晰的认知：

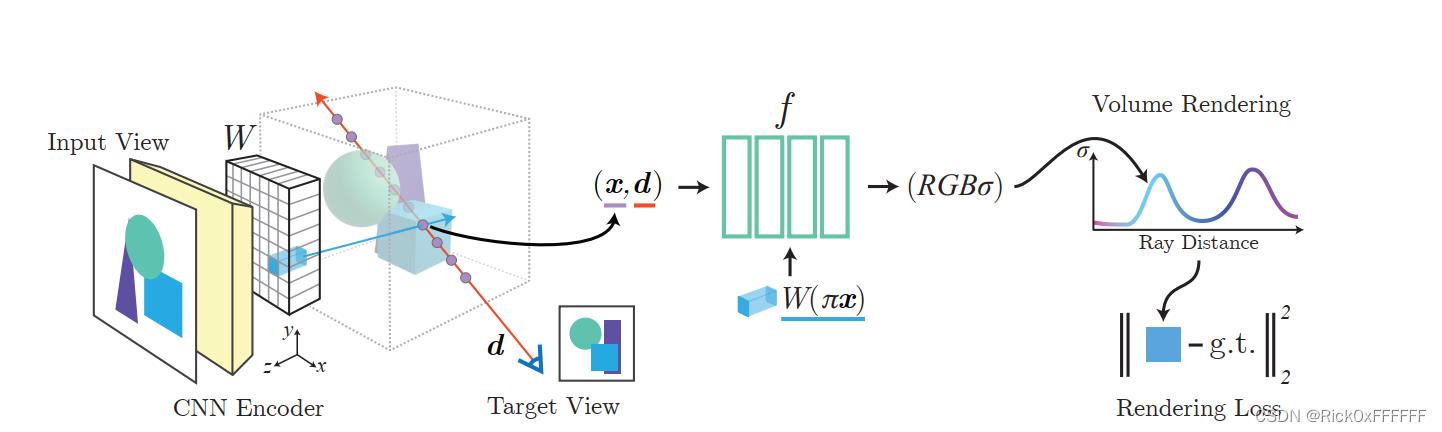
首先该图分为三部分，分别是：

• CNN对图像进行编码
• NeRF网络inference: $(\mathbf{x},\mathbf{d},I)\to (\mathbf{c},\sigma )$
• Volume Rendering

CNN Encoder:编码图像得到一个feature 图，WHF, F是feature数量，将输出结果命名为$W$，$\pi$是一个将3维空间的点$x$映射到二维图像上的点(u,v)的映射函数，则$W(\pi (x))$就表示三维点$\mathbf{x}$对应的二维像素的feature了

NeRF Network:
$$f(\gamma (\mathbf{x}),\mathbf{d};\mathbf{W}(\pi (x)))=(\sigma ,\mathbf{c})$$

其中$\gamma (\mathbf{x})$是position encoding。

Volume Rendering:和经典NeRF一致。

Incorporating Multiple Views

作者希望通过融合多视角下的观测来构建出更为逼真的三维表达。 如何融合呢？对于一个世界坐标系下的query point $\mathbf{x}$ ，以及它的view direction $\mathbf{d}$, 给定N个相机视角，以及它的位姿：
$${\mathbf{P}}^{(i)}=[{\mathbf{R}}^{(i)}{\mathbf{t}}^{(i)}]$$
通过位姿变换，就可以求解出每个相机坐标系下$x$的位姿了：
$${\mathbf{x}}^{(}i)={\mathbf{P}}^{(i)}\mathbf{x},{\mathbf{d}}^{(i)}={\mathbf{R}}^{(i)}\mathbf{d}$$

作者在此将NeRF做了一个层级划分，采用了PointNet之类的思想，先通过一个initial layers（命名为$f_1$）获得一个中间向量：
$${\mathbf{V}}^{(i)}=f_1(\gamma ({\mathbf{x}}^{(i)}),{\mathbf{d}}^{(i)};{\mathbf{W}}^{(i)})$$
随后利用pooling 操作$\psi$将多个中间向量融合在一起:
$$(\sigma ,\mathbf{c})=f_2(\psi ({\mathbf{V}}^{(1)}),\psi ({\mathbf{V}}^{(2)}),...,\psi ({\mathbf{V}}^{(n)}))$$

Result

效果不错：

好多文章都在用PixelNeRF: SceneRF, AutoRF等等，强推！要是喜欢本文就点个赞吧~

参考文献

Yu, Alex, et al. “pixelnerf: Neural radiance fields from one or few images.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.

辐射神经场算法——Wild-NeRF / Mipi-NeRF / BARF / NSVF / Semantic-NeRF / DSNeRF

辐射神经场算法——NeRF++ / Wild-NeRF / Mipi-NeRF / BARF / NSVF / Semantic-NeRF

• 辐射神经场算法——NeRF++ / Wild-NeRF / Mip-NeRF / BARF /NSVF / Semantic-NeRF / DSNeRF
• • 1. NeRF++
  • 2. Wild-NeRF
  • 3. Mip-NeRF
  • 4. BARF
  • 5. NSVF
  • 6. Semantic-NeRF

辐射神经场算法——NeRF++ / Wild-NeRF / Mip-NeRF / BARF /NSVF / Semantic-NeRF / DSNeRF

原始的NeRF虽然效果很惊艳，但是其一个场景少则一两天的训练速度，以及对于输入图像质量和位姿的要求却不尽人意，因此，在NeRF提出来很短的时间内就衍生出了各种基于NeRF优化的方法，本文主要是对这些方法进行一个简单总结，但是建议先了解原始NeRF的算法原理再来阅读本博客，对于原始NeRF算法的介绍可以参考博客辐射神经场算法——NeRF算法详解

1. NeRF++

NeRF++原论文名为《NeRF++: Analyzing and Improving Nerual Radiance Fileds》，该论文主要包括两部分：一部分是分析了原始NeRF具备的Shape-Radiance Ambiguity问题，另一部分是提出了一个解决室外360度开放场景的渲染方案。

首先针对Shape-Radiance Ambiguity问题，作者做了如下一个实验：

作者先使用一个球形的模型去训练NeRF中的$\sigma$，然后再使用上左中的GT training view去训练NeRF中的$\mathbf{c}$，在相同视角下进行预测时发现即使在错误的$\sigma$分布下仍然能输出较好的图像质量，但是一旦更换视角（GT test view）就会输出如上左图的结果。造成该现象的原因正是View-Dependent的网络设计。但是如果我们一旦修改网络设计，将采样点的位置$x$和方向$\mathbf{d}$都从网络的第一层输入的话，网络整体效果就会下降，如下图所示：

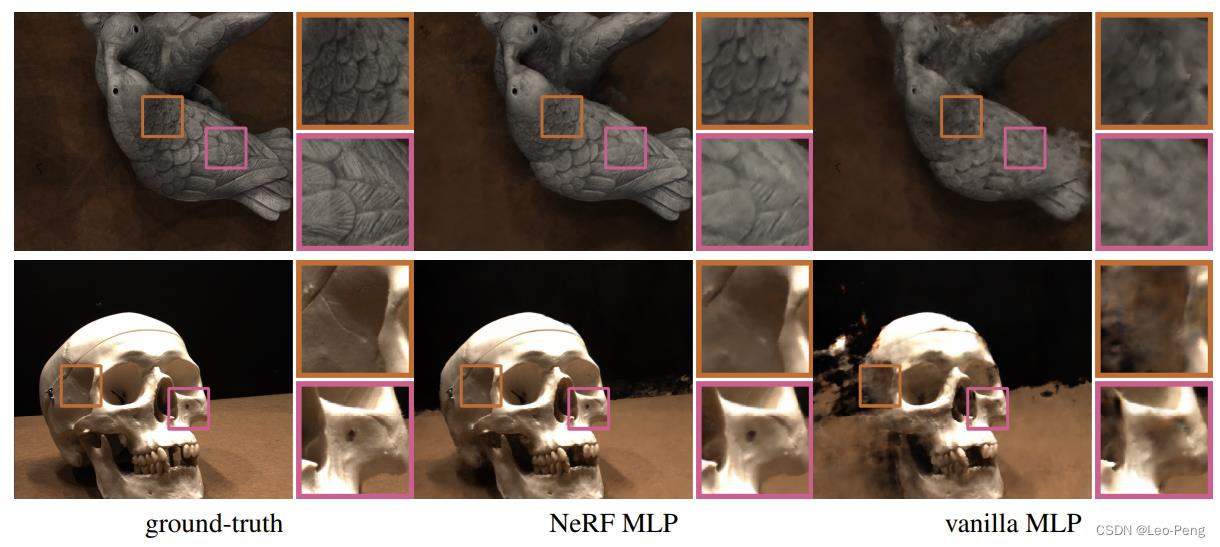
文章的第二部分介绍的室外360度开放场景的一种解决方案，在原始NeRF中，对于Front-View的开放场景，使用的一种名为NDT坐标系的方式（可以简单理解为逆深度），但是对于360度的开放场景NDT坐标系是搞不定的，因此作者提出了将360度开放场景的渲染分为两部分通过两个NeRF进行渲染，如下所示：

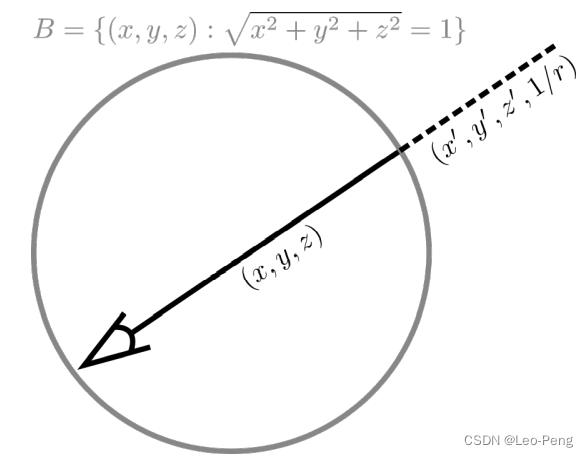
规定一个球体$B=(x,y,z):\sqrt{x^2+y^2+z^2}=1$:
球体内保持欧拉坐标系$(x,y,z)$，使用原始的NeRF用于渲染前景部分;
球体外通过一个四维向量$\left(x^{\prime },y^{\prime },z^{\prime },1/r\right)$表示，用于渲染背景部分，其中$x^{\prime 2}+y^{\prime 2}+z^{\prime 2}=1$用于表示方向，$0<1/r<1$用于表示距离，并且$x^{\prime },y^{\prime },z^{\prime }\in [-1,1],1/r\in [0,1]$，用于进行背景渲染的NeRF输入为$\left(x^{\prime },y^{\prime },z^{\prime },1/r\right)$，输出则是${\sigma }_{\text{out }},{\mathbf{c}}_{\text{out }}$.

那么接下来的问题就是当我们给定一个像素的射线$\mathbf{r}=\mathbf{o}+t\mathbf{d}$，当采样点位于球体外时如何求得四维向量$\left(x^{\prime },y^{\prime },z^{\prime },1/r\right)$呢？如下图所示：

我们给定不同采样点$\mathbf{p}$得到不同的半径$r$，那么如果获得$x^{\prime },y^{\prime },z^{\prime }$呢？上图中点$\mathbf{a}=\mathbf{o}+t_a\mathbf{d}$，我们令$\left|\mathbf{o}+t_a\mathbf{d}\right|=1$就可以求得点$\mathbf{a}$的坐标，同理点$\mathbf{b}=\mathbf{o}+t_b\mathbf{d}$可以通过${\mathbf{d}}^T\left(\mathbf{o}+t_b\mathbf{d}\right)=0$求得，那么我们根据$\omega =\arcsin |\mathbf{b}|-\arcsin \left(|\mathbf{b}|\cdot \frac{1}{r}\right)$即可以对点$\mathbf{a}$方向进行渲染既可以得到点$\mathbf{p}$的方向$x^{\prime },y^{\prime },z^{\prime }$，其实就是一个很简单的几何求解。解决了这个问题后就可以给出最后NeRF++的计算公式：
$$\begin{array}{rl}\mathbf{C}(\mathbf{r})=& \underset{\text{(i) }}{\underbrace{{\int }_{t=0}^{t^{\prime }}\sigma (\mathbf{o}+t\mathbf{d})\cdot \mathbf{c}(\mathbf{o}+t\mathbf{d},\mathbf{d})\cdot e^{-}}}\\ & \end{array}$$

深度学习综述（下载PDF版）

深度学习CV领域必读论文

计图：5秒训好NeRF！已开源

论文笔记：Depth-supervised NeRF: Fewer Views and Faster Training for Free

钛智能 | 李彦宏：PaddlePaddle不如TensorFlow | ABCD每日必读 · 0826

“深度学习”到底是什么？这篇文章讲明白了