蓝桥杯刷题总结(省)
Posted psudd
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯刷题总结(省)相关的知识,希望对你有一定的参考价值。
文章目录
1. 正确率优先
关键1 —— 正确率优先:题目数量有限,并且无法及时得到结果验证。所以一定要先审题 + 多组测试数据检验(或者直接输出求解过程验证),正确率永远是第一位的。
一定要首先保证正确率,题目数量有限并且压轴的思维题有难度可以少写两个都无关紧要,正确率永远是第一位。
关键2 —— 审题必须仔细,相关数是否有大小,倍数等要求,结果的输出一般都会要求唯一(按照字典序结果输出等等), 一定要注意限制条件。
2. 高精度模板
题目描述:

题目链接: 乘积尾0
分析过程:
这个题目的优化思路是将整数进行质因数 2 和 5 的分解,最后去求有多少对完整的2和5就会产生多少个10
但建议能暴力求解的就直接进行暴力求解,因为暴力求解省去了分析思考的过程,这里我们可以直接套用高精度模板进行连乘得到结果.
运行代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
vector<int> mul(vector<int> a, int b)
vector<int> c;
int sum = 0;
for(int i = 0; i < a.size() || sum; i ++ )
if(i < a.size()) sum += a[i] * b; // 保证范围 < a.size() 才可以乘
c.push_back(sum % 10);
sum /= 10;
while(c.size() > 0 && c.back() == 0) c.pop_back(); // 清楚后导0
return c;
int main()
vector<int> v;
v.push_back(1);
for(int i = 0; i < 100; i ++ )
int x;
cin >> x;
v = mul(v, x);
int ret = 0;
for(int i = 0; i < v.size(); i ++ )
if(v[i] == 0) ret ++;
else break;
cout << ret;
return 0;
3. 前缀和模板 —— 保证不要出现数据0
题目描述:

题目链接: 递增三元组
分析过程:
总体思路:先求出 sa[x] 表示 a 数组当中小于等于 x 的元素的个数,再去求 sb[x] 表示数组 b 当中小于等于 x 的元素方案数(可以合法连接上a组当中元素),最后求c 数组直接进行连接即可。
关键:通常我们想要让元素大小从1开始,因为这样我们就不必要对首个元素进行特判处理(如果从0开始不能直接操作 f[x] = f[x] + f[x - 1]),所以我们为了不必要进行特判,所以我们可以让元素全部自加一下,保证最小的元素大小都1.
关键:必须要自加,否则对元素处理的时候会出现错误。例如此题sb[0]是b元素为0能合法连接a的方案数,如果未自加如果b组出现0,sb[0] != 0,这里在之后的递归上面会出现大错误
前缀和为实现元素统一处理(直接从1开始):保证不要出现数据0
运行代码:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL sa[N], sb[N];
int main()
int n, x;
scanf("%d", &n);
for(int i = 0; i < n; i ++ )
scanf("%d", &x);
sa[++ x] ++;
for(int i = 1; i < N; i ++ ) sa[i] += sa[i - 1];
for(int i = 0; i < n; i ++ )
scanf("%d", &x);
sb[++ x] ++ ;
for(int i = 1; i < N; i ++ ) sb[i] = sb[i] * sa[i - 1] + sb[i - 1];
LL ret = 0;
for(int i = 0; i < n; i ++ )
scanf("%d", &x);
ret += sb[(x + 1) - 1];
cout << ret;
return 0;
4. 状态转移模板
题目描述:

题目链接: 积木画
分析过程:
关键:f[ i ][ j ] 表示处理完前 i - 1 列 且第 i 列状态为 j 的方案数
关键:列出状态转移的方程 + 枚举状态转移 + 结果往往为f[n + 1][0] (处理完前 n 列)
运行代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
const int mod = 1000000007;
int f[2][4];
int to[4][4] = // 状态转移
1, 1, 1, 1,
0, 0, 1, 1,
0, 1, 0, 1,
1, 0, 0, 0
;
int main()
int n;
cin >> n;
f[1][0] = 1;
for(int i = 2; i <= n + 1; i ++ )
memset(f[i & 1], 0, sizeof(f[0])); // 注意清空本层数据
for(int j = 0; j < 4; j ++ ) // 得到状态 j , 从上层四个状态 k 依次判断能否转换
for(int k = 0; k < 4; k ++ )
f[i & 1][j] = (f[i & 1][j] + f[i - 1 & 1][k] * to[k][j]) % mod;
cout << f[n + 1 & 1][0]; // 结果一定是处理完前 n 层的结果
return 0;
5. 哈希模板
题目描述:

题目链接: 扫雷
分析过程:
关键:将x, y坐标映射成一个唯一的哈希值,记录下该哈希值键对应的炸弹编号和访问状态
运行代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<set>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
const int M = 999997, N = 5e4 + 10;
struct Cir
int x, y, r;
cir[N];
LL h[M];
int id[M];
bool st[M];
int sqr(int x)
return x * x;
LL get_hash(int x, int y)
return 1000000001ll * x + y;
int get_key(int x, int y)
LL hash = get_hash(x, y);
int key = (hash % M + hash) % M;
while(h[key] != -1 && h[key] != hash)
if(++ key == M) key = 0;
return key;
void dfs(int x, int y, int r)
int key = get_key(x, y);
st[key] = true;
for(int i = x - r; i <= x + r; i ++ )
for(int j = y - r; j <= y + r; j ++ )
int key = get_key(i, j);
if(id[key] && !st[key] && sqr(x - i) + sqr(y - j) <= sqr(r)) dfs(i, j, cir[id[key]].r);
int main()
memset(h, -1, sizeof(h));
int n, m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ )
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
cir[i] = x, y, r;
int key = get_key(x, y);
h[key] = get_hash(x, y);
if(id[key] == 0 || r > cir[id[key]].r ) id[key] = i;
while(m -- )
int x, y, r;
scanf("%d%d%d", &x, &y, &r);
for(int i = x - r; i <= x + r; i ++ )
for(int j = y - r; j <= y + r; j ++ )
int key = get_key(i, j);
if(id[key] && !st[key] && sqr(x - i) + sqr(y - j) <= sqr(r)) dfs(i, j, cir[id[key]].r);
int ret = 0;
for(int i = 1; i <= n; i ++ )
int key = get_key(cir[i].x, cir[i].y);
if(st[key]) ret ++;
cout << ret;
return 0;
6. sqrt()函数 —— 大数 long double 转换
题目描述:

题目链接: 砍竹子
分析过程:
关键:大数开根号的时候使用sqrtl()函数,将默认数据类型提到 long double,防止出现误差
关键:也可以使用sqrt()函数,但是要在数之前加入一个long double的强制数据类型转换也可以要不然sqrt()函数本身在c++ 11里面它可以匹配(double, long double)并不会自动提升数据精度
运行代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<set>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
LL f[N][10];
int main()
int n, mx = -1, ret = 0;
scanf("%d", &n);
for(int i = 0; i < n; i ++ )
LL x, top = 0, stk[10];
scanf("%lld", &x);
while(x > 1) stk[++ top] = x, x = sqrt((long double)(x / 2 + 1));
mx = max(mx, (int)top);
ret += top;
for(int j = 0, k = top; k; j ++ , k --) f[i][j] = stk[k];
for(int i = 0; i < mx; i ++ )
for(int j = 1; j < n; j ++ )
if(f[j][i] && f[j][i] == f[j - 1][i]) ret --;
cout << ret;
return 0;
7. 直线斜率与截距 —— 利用 a b 关系直接求
题目描述:

题目链接: 直线
分析过程:
关键:求直线的斜率和截距。注意因为浮点数类型本身就会造成误差,所以尽可能使用题目本身的变量直接计算相关结果,不要利用求得的浮点数再去求解结果.
关键:利用 y = k * x + b ,消去 k 得到 b,再消去 b 得到 k, 不要利用间接得到的 k 求 b
运行代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<set>
#include<vector>
using namespace std;
typedef long double LD;
typedef pair<LD, LD> PLL;
set<PLL> s;
bool check(int x1, int y1, int x2, int y2)
LD k = (LD)(y2 - y1) / (x2 - x1);
LD b = (LD)(y1 * x2 - y2 * x1) / (x2 - x1);
if(s.count(k, b) != 0)
return false;
else
s.insert(k, b);
return true第十三届蓝桥杯第二场模拟赛题解
马上到蓝桥杯了,虽然省赛简单化,但是刷题是不可或缺的,下面我会更新蓝桥杯刷题题解,一起冲进国赛
文章目录
前言
马上到蓝桥杯了,虽然省赛简单化,但是刷题是不可或缺的,下面我会更新蓝桥杯刷题题解,一起冲进国赛
提示:以下是本篇文章正文内容,下面案例可供参考
填空题
第一题

0-255 所以最大为255
第二题

直接利用gcd求解最大公约数即可
import gmpy2
count=0
for i in range(2,2022):
if(gmpy2.gcd(2021,i)!=1):
count+=1
print(count)
答案:89
第三题

暴力解法求解, i=jj-kk
进而得出 i=(j-k)*(j+k)所以j-k一定是大于0的 所以j>k
i=( 一个正数)*j+k
所以j一定小于i的,所以遍历即可
count=0
flag=0
for i in range(2022):
flag=0
for j in range(2022):
if(flag==1):
break
for k in range(j):
if(flag==0):
if(i==j*j-k*k):
count+=1
flag=1
break
else:
continue
print(count)
答案是
1516
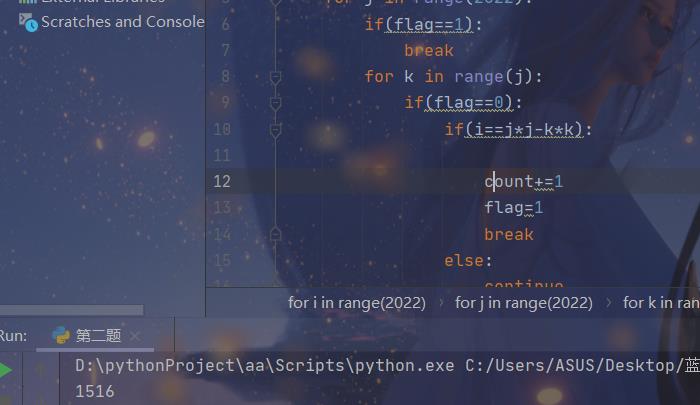
第四题
问题描述
小蓝要用01串来表达一段文字,这段文字包含 a, b, c, d, e, f 共 6 个字母,每个字母出现的次数依次为:a 出现 10次,b 出现 20 次,c 出现 3 次,d 出现 4 次,e 出现 18 次,f 出现 50 次。
小蓝准备分别对每个字母使用确定的01串来表示,不同字母的01串长度可以不相同。
在表示文字时,将每个字母对应的01串直接连接起来组成最终的01串。为了能够正常还原出文字,小蓝的编码必须是前缀码,即任何一个字符对应的01串都不能是另一个字符对应的01串的前缀。
例如,以下是一个有效的编码:
a: 000
b: 111
c: 01
d: 001
e: 110
f: 100
其中 c 的长度为 2,其它字母的编码长度为
3,这种方式表示这段文字需要的总长度为:103+203+32+43+183+503=312。上面的编码显然不是最优的,将上面的 f
的编码改为 10,仍然满足条件,但是总长度为 262,要短
50。要想编码后的总长度尽量小,应当让出现次数多的字符对应的编码短,出现次数少的字符对应的编码长。请问,在最优情况下,编码后的总长度最少是多少?
代码如下(示例):
一看就是哈夫曼编码,这里由于是填空题,直接手算就行了,多的距离近,少的距离远
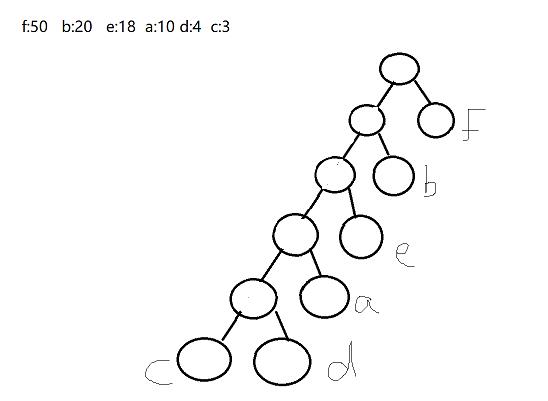
计算如下
50*1+2*20*3*18+10*4*4+4*3
数据结构哈夫曼知识了
画个图手算一下就有了
第五题
下面的矩阵中包含 ABCDEF 六种字符,请问出现最多的字符出现了几次?
FFEEFEAAECFFBDBFBCDA
DACDEEDCCFFAFADEFBBA
FDCDDCDBFEFCEDDBFDBE
EFCAAEECEECDCDECADDC
DFAEACECFEADCBFECADF
DFBAAADCFAFFCEADFDDA
EAFAFFDEFECEDEEEDFBD
BFDDFFBCFACECEDCAFAF
EFAFCDBDCCBCCEADADAE
BAFBACACBFCBABFDAFBE
FCFDCFBCEDCEAFBCDBDD
BDEFCAAAACCFFCBBAAEE
CFEFCFDEEDCACDACECFF
BAAAFACDBFFAEFFCCCDB
FADDDBEBCBEEDDECFAFF
CDEAFBCBBCBAEDFDBEBB
BBABBFDECBCEFAABCBCF
FBDBACCFFABEAEBEACBB
DCBCCFADDCACFDEDECCC
BFAFCBFECAACAFBCFBAF
data = pd.read_csv(
‘https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv’)
print(data.head())
利用collect来进行统计
```python
from collections import Counter
s='FFEEFEAAECFFBDBFBCDADACDEEDCCFFAFADEFBBAFDCDDCDBFEFCEDDBFDBEEFCAAEECEECDCDECADDCDFAEACECFEADCBFECADFDFBAAADCFAFFCEADFDDAEAFAFFDEFECEDEEEDFBDBFDDFFBCFACECEDCAFAFEFAFCDBDCCBCCEADADAEBAFBACACBFCBABFDAFBEFCFDCFBCEDCEAFBCDBDDBDEFCAAAACCFFCBBAAEECFEFCFDEEDCACDACECFFBAAAFACDBFFAEFFCCCDBFADDDBEBCBEEDDECFAFFCDEAFBCBBCBAEDFDBEBBBBABBFDECBCEFAABCBCFFBDBACCFFABEAEBEACBBDCBCCFADDCACFDEDECCCBFAFCBFECAACAFBCFBAF'
s=Counter(s)
s1=dict(s)
print(s1.values())
答案是78
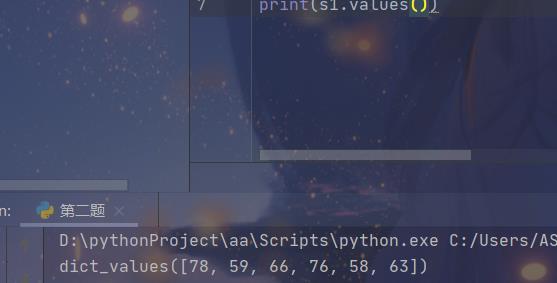
第六题
问题描述
小蓝要到店里买铅笔。铅笔必须一整盒一整盒买,一整盒 12 支,价格 p 元。小蓝至少要买 t 支铅笔,请问他最少花多少钱?
输入格式
输入一行包含两个整数 p、t,用一个空格分隔。
输出格式
输出一行包含一个整数,表示答案。
样例输入
5 30
样例输出
15
样例说明
小蓝至少要买3盒才能保证买到30支铅笔,总共花费 15 元。
评测用例规模与约定
对于所有评测用例,1 <= p <= 100,1 <= t <= 10000
除数问题
list1= input('输入一行包含两个整数 p、t,用一个空格分隔').split(' ')
a=int(list1[0])
b=int(list1[1])
if(b%12==0):
print(b//12*a)
else:
print((b//12+1)*a)
第七题
问题描述
给定一个三角形的三条边的长度 a, b, c,请问这个三角形是不是一个直角三角形。
输入格式
输入一行包含三个整数 a, b, c,表示三角形三边的长度,相邻整数之间用一个空格分隔。
输出格式
如果是直角三角形,输出“YES”(全大写),否则输出“NO”(全大写)。
样例输入
3 4 5
样例输出
YES
样例输入
4 5 4
样例输出
NO
评测用例规模与约定
对于所有评测用例,1 <= a, b, c <= 1000。
一共三种情况:
a*a+b*b==c*c
a*a+c*c==b*b
a*a==c*c+b*b
```python
list1=input('输入一行包含三个整数 a, b, c,表示三角形三边的长').split(' ')
a=int(list1[0])
b=int(list1[1])
c=int(list1[2])
if(a*a+b*b==c*c or a*a+c*c==b*b or a*a==c*c+b*b):
print('YES')
else:
print("NO")
加个条件过去就行了
第八题
问题描述
n 个小朋友正在做一个游戏,每个人要分享一个自己的小秘密。 每个小朋友都有一个 1 到 n 的编号,编号不重复。
为了让这个游戏更有趣,老师给每个小朋友发了一张卡片,上面有一个 1 到 n 的数字,每个数字正好出现一次。
每个小朋友都将自己的秘密写在纸上,然后根据老师发的卡片上的数字将秘密传递给对应编号的小朋友。如果老师发给自己的数字正好是自己的编号,这个秘密就留在自己手里。
小朋友们拿到其他人的秘密后会记下这个秘密,老师会再指挥所有小朋友将手中的秘密继续传递,仍然根据老师发的卡片上的数字将秘密传递给对应编号的小朋友。
这样不断重复 n 次。 现在,每个小朋友都记下了很多个秘密。
老师现在想找一些小朋友,能说出所有秘密,请问老师最少要找几个小朋友?
输入格式
输入的第一行包含一个整数 n。 第二行包含 n 个整数 a[1], a[2], …,
a[n],相邻的整数间用空格分隔,分别表示编号 1 到 n 的小朋友收到的数字。
输出格式
输出一行包含一个整数,表示答案。
样例输入
6 2 1 3 5 6 4
样例输出
3
样例说明
最终小朋友 1, 2 互相知道了对方的秘密,小朋友 3 只知道自己的秘密,小朋友 4, 5, 6 互相知道了对方的秘密。 至少要找
3 个小朋友才能说出所有秘密。
评测用例规模与约定
对于 30% 的评测用例,2 <= n <= 30。 对于 60% 的评测用例,2 <= n <= 1000。
对于所有评测用例,2 <= n <= 100000。
————————————————
我们这里利用填坑思想,如果 遍历过程就是遍历signal数组的过程,并将其填1 如果已经是1了那末就+1,因为要想知道对方秘密,那末一定是能按照标志能便利所有了,如果中断了那末就将结果+1
n=5
temp=[]
count=0
s='2 3 1 5 4'.split(' ')
print(s)
sigal=n*[0]
p=int(s[0])-1
ee=0
while 1:
if(sigal[p]!=1):
sigal[p]=1
p=int(s[p])-1
ee+=1
if(ee==n):
break
else:
p = int(s[ee])-1
print(sigal)
count+=1
print(count+1)
最后一次没有循环,所以结果再加一就行了
以上是关于蓝桥杯刷题总结(省)的主要内容,如果未能解决你的问题,请参考以下文章