AR 预测模型的 Matlab 实现（超详细建模流程）

Posted 图灵猫

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了AR 预测模型的 Matlab 实现（超详细建模流程）相关的知识，希望对你有一定的参考价值。

AR 预测模型的 Matlab 实现

时间序列模型建模流程图

Y N Y N Y Y Y N 获得观察值序列 白噪声检验 结束 平稳性检验 模型识别 平稳化处理 参数估计 模型检验 序列预测

相关链接:
自协方差函数的 Matlab 实现
时间序列平稳化的 8 种方法比较及 Matlab 实现
AR 模型的预测课件
AR 模型的预测课件(附最小二乘原理)
程序源代码打包下载

开发环境

------------------------------------------------------------------------------------------------
MATLAB 版本: 9.12.0.1884302 (R2022a)
MATLAB 许可证编号: 968398
操作系统: macOS  Version: 12.3 Build: 21E230 
Java 版本: Java 1.8.0_202-b08 with Oracle Corporation Java HotSpot(TM) 64-Bit Server VM mixed mode
------------------------------------------------------------------------------------------------

读取数据

上证指数数据集:SH600031.csv

该数据集描述了三一重工 2017 年每日的开盘、最高、最低、收盘、成交量、成交额.

下面取连续500次成交量的观测数据进行建立时间序列模型并预测.

前 10 行数据预览


    "2017/01/03"    "09:35"    "6.10"    "6.14"    "6.10"    "6.13"    "2851.00"    "1745600.00"
    "2017/01/03"    "09:40"    "6.13"    "6.13"    "6.11"    "6.13"    "1413.00"    "865200.00" 
    "2017/01/03"    "09:45"    "6.13"    "6.18"    "6.12"    "6.18"    "5662.00"    "3487800.00"
    "2017/01/03"    "09:50"    "6.18"    "6.19"    "6.17"    "6.18"    "4891.00"    "3022800.00"
    "2017/01/03"    "09:55"    "6.17"    "6.18"    "6.17"    "6.18"    "3300.00"    "2038900.00"
    "2017/01/03"    "10:00"    "6.18"    "6.18"    "6.17"    "6.17"    "2649.00"    "1635400.00"
    "2017/01/03"    "10:05"    "6.17"    "6.18"    "6.16"    "6.16"    "3107.00"    "1917000.00"
    "2017/01/03"    "10:10"    "6.17"    "6.18"    "6.16"    "6.18"    "5671.00"    "3499300.00"
    "2017/01/03"    "10:15"    "6.18"    "6.19"    "6.17"    "6.18"    "6490.00"    "4011200.00"
    "2017/01/03"    "10:20"    "6.19"    "6.19"    "6.17"    "6.17"    "3041.00"    "1877400.00"

程序源代码

clc,clear
%% 读取数据
filename='SH600031.csv';
Data = readmatrix(filename, 'OutputType', 'string');
data = str2double(Data(1:500,7));
N = length(data);

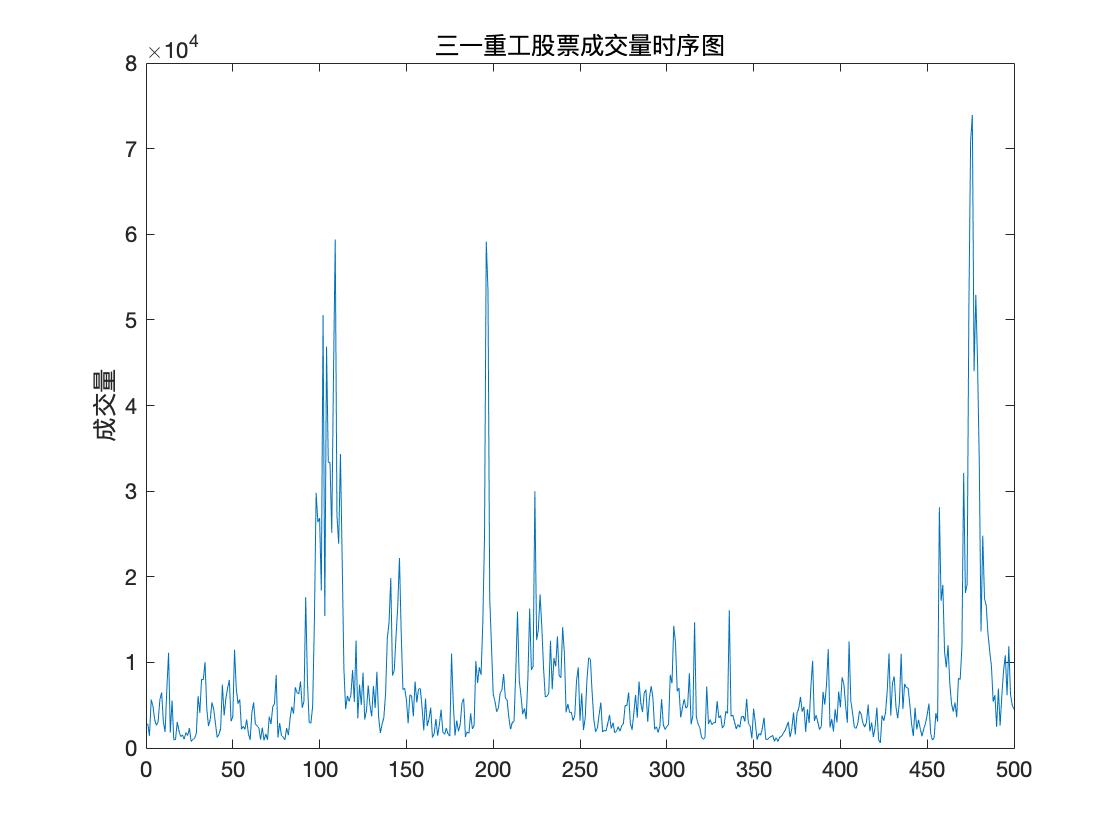
原数据可视化

程序源代码

%% 原数据可视化
figure(1)
plot(data);
title('三一重工股票成交量时序图')
ylabel('成交量')
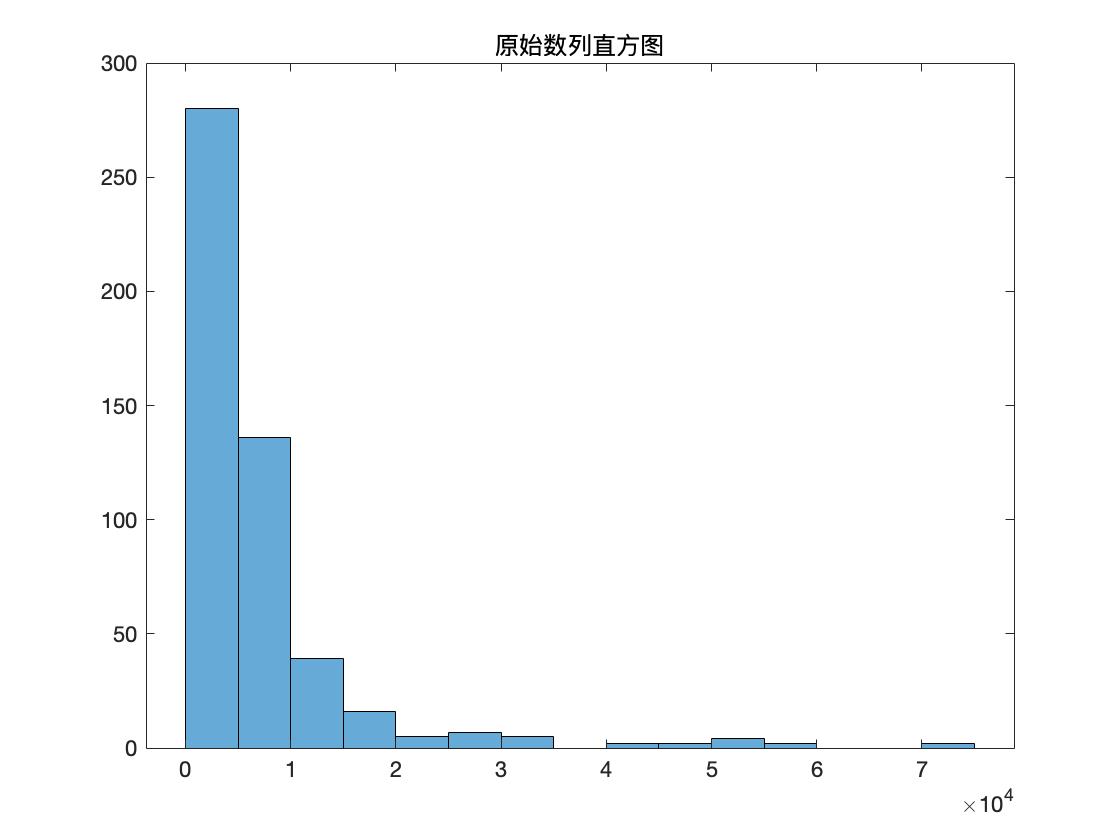
figure(2)
histogram(data);
title('原始数列直方图')

划分训练集和验证集

因为要对数据进行预测,所以我们将数据分为 70% 的训练集及 30% 的测试集.

程序源代码

%% 划分训练集和测试集
trg = round(0.7*N);
TrainData = data(1:trg);
TestData = data(trg+1:end);

数据白噪声检验

程序源代码

%% 数据白噪声检验
disp('数据白噪声检验')
[hLBQ,pLBQ] = lbqtest(TrainData);
disp('检验结果如下')
hLBQ,pLBQ

命令行窗口输出

数据白噪声检验
检验结果如下

hLBQ =

  logical

   1


pLBQ =

     0

输出变量说明:

hLBQ 表示测试的结果

hLBQ = 1 表示拒绝数据无自相关的零假设而选择备择假设.(非白噪声序列)

hLBQ = 0 表示接受数据无自相关的零假设.(白噪声序列)

pLBQ 表示 lb 检验统计量的概率 p 值.

数据平稳性检验

程序源代码

%% 数据平稳性检验
disp('使用 PP 检验, 如果不能拒绝原假设, 则说明序列存在单位根')
[hp,hpValue,stat,cValue,reg] = pptest(TrainData,'model','Ts');
disp('检验结果如下:')
hp,hpValue
diff = 0;
while hp == 0
    disp('hp=0,说明原始序列不平稳')
    disp('对序列作差分处理,再对差分数据进行 PP 检验,检验结果如下:')
    smooth_data = diff(TrainData);
%     % 去除趋势(线性拟合)
%     smooth_data=trend_fitting(smooth_data');
%     % 去除趋势(多项式拟合)
%     smooth_data = polynomial_fitting(smooth_data',4);
%     % 去周期(季节分析)
%     [smooth_data,I]= seasonal_analysis(smooth_data',12);
%     % 去除趋势(k 阶差分)
%     smooth_data= difference(smooth_data,1);
%     % 去周期(k 步季节差分)
    smooth_data= seasonal_difference(smooth_data,12);
    [hp,hpValue,stat,cValue,reg] = pptest(smooth_data,'model','Ts');
    hp,hpValue
    diff = diff + 1;
end
disp('hp=1,原始序列平稳')
smooth_data = TrainData;

命令行窗口输出

使用 PP 检验, 如果不能拒绝原假设, 则说明序列存在单位根
检验结果如下:

hp =

  logical

   1


hpValue =

   1.0000e-03

hp=1,原始序列平稳

模型识别

自相关及偏自相关图像

程序源代码

%% 自相关及偏自相关图像
%原序列图片
figure(3)
subplot(2,1,1)
autocorr(TrainData);
title('成交量的自相关图像')
subplot(2,1,2)
parcorr(TrainData)
title('成交量的偏自相关图像')
if diff >=1
    % 平滑化后图片
    figure(4)
    subplot(2,1,1)
    autocorr(smooth_data);
    title('平稳化后的自相关图像')
    subplot(2,1,2)
    parcorr(smooth_data)
    title('平稳化后的偏自相关图像')
end

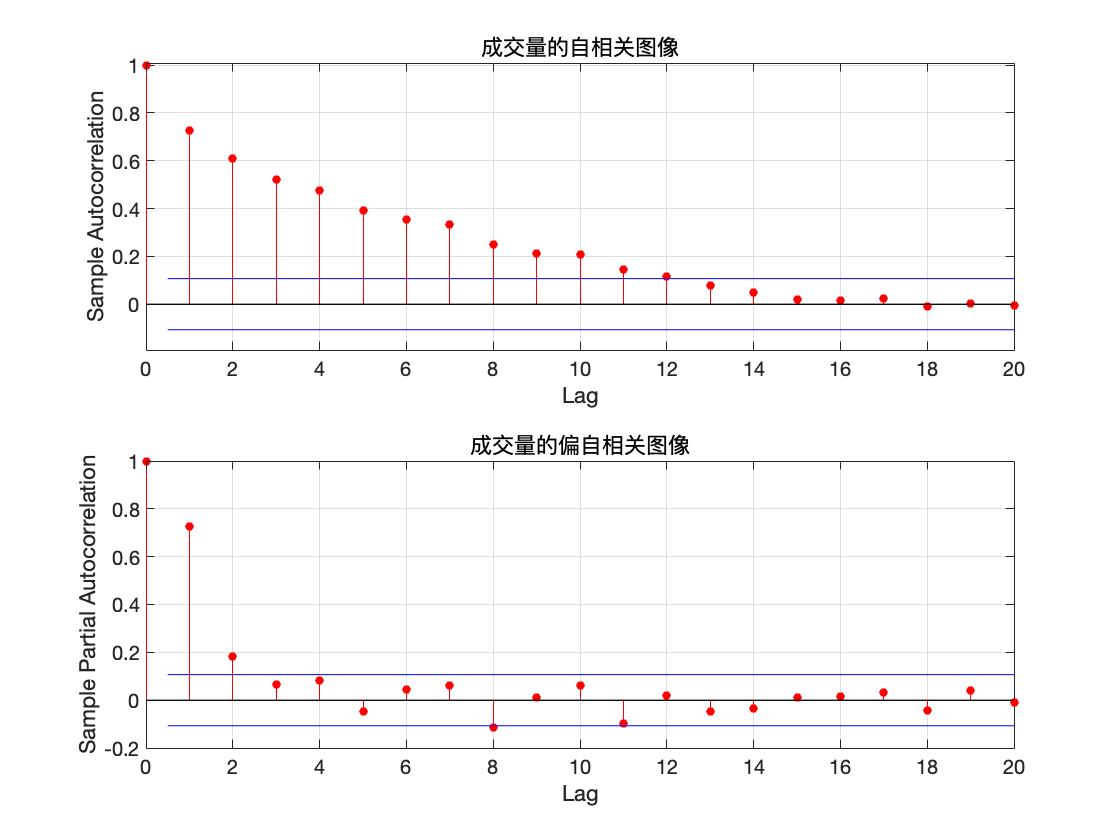
从自相关及偏自相关图像可以看出, 自相关系数缓慢衰减,可以判定自相关系数拖尾,而偏自相关系数在延迟 2 阶后都在2 倍标准差范围里面. 可以认为 2 阶后偏自相关系数为零, 所以偏自相关系数 2 阶后截尾, 由 AR 模型的统计特性,可以初步判定该数据是 AR(2) 模型.

AIC & BIC 准则定阶

在对 AR 模型识别时, 根据其样本偏自相关系数的截尾步数, 可初步得到 A R \\mathrmAR AR 模型的阶数 p p p. 然而, 此时建立的 AR ⁡ ( p ) \\operatornameAR(p) AR(p) 模型末必是最优的. 一个好模型通常要求残差序列方差较小, 同时模型也相对简单, 即要求阶数较低. 因此, 我们需要一些准则来比较不同阶数的模型之间的优劣, 从而确定最合适的阶数.

  1. Akaike 信息准则

Akaike 信息准则, 简称为 AIC 准则, 是一种基于观测数据选择最优参数模型的信息准则, 它既要衡量模型对原始数据的拟合程度, 又要考虑模型中所含待估参数的个数, 即模型的复杂程度.

定义 AIC 信息准则如下:
AIC ⁡ ( p ) = ln ⁡ σ ^ 2 + 2 ( p + 1 ) N , \\operatornameAIC(p)=\\ln \\hat\\sigma^2+\\frac2(p+1)N, AIC(p)=lnσ^2+N2(p+1)​,
其中 p + 1 p+1 p+1 为待估参数个数, 即 AR ⁡ ( p ) \\operatornameAR(p) AR(p) 模型的 p p p 个自回归系数 a 1 , ⋯   , a p a_1, \\cdots, a_p a1​,⋯,ap​ 以及随机误差的方差 σ 2 \\sigma^2 σ2.

程序源代码

%% AIC 准则定阶
maxLags = 8;
AIC = zeros(maxLags,1);
for j=1:maxLags
    mdl = ar(smooth_data,j);
    AIC(j) = mdl.Report.Fit.AIC;
end
% 画热度图来表示 AIC 数值的分布
figure(4)
heatmap(AIC/1000);
xlabel("AIC")
ylabel("AR Lags")
OptimalARLags_AIC = find(AIC==min(AIC));
title('Optimal AR ')

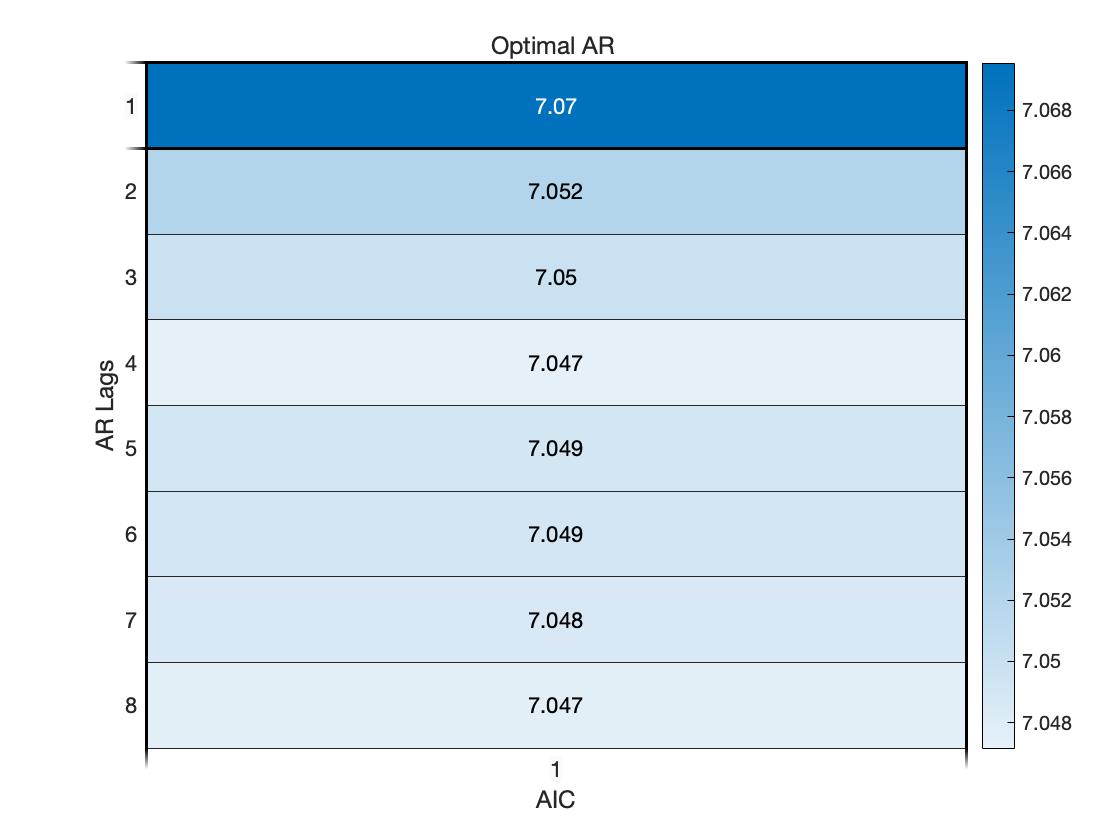
AIC 准则下的最优 AR 模型的阶数为 4 阶.

  1. BIC 准则

模拟研究结果表明, 当观测序列长度 N N N 较大时, AIC 准则有使 p p p 值估计 过高的倾向. 通过修正拟合残差方差和拟合模型参数个数之间的权重, 得到贝叶斯信息准则, 简称为 BIC 准则, 其定义如下:
B I C ( p ) = ln ⁡ σ ^ 2 + ln ⁡ N ( p + 1 ) N . \\mathrmBIC(p)=\\ln \\hat\\sigma^2+\\frac\\ln N(p+1)N . BIC(p)=lnσ^2+NlnN(p+1)​.
A I C \\mathrmAIC AIC 准则与 BIC 准则的差异仅在于将 A I C \\mathrmAIC AIC 中后一项中的 2 换为 ln ⁡ N \\ln N lnN, 而这一项表示模型阶数 p p p 对 AIC 和 BIC 取值大小的作用, 2 和 ln ⁡ N \\ln N lnN 相当于对 p p p 的加权系数. 当 N N N 较大时, 有 ln ⁡ N ≫ 2 \\ln N \\gg 2 lnN≫2, 因此在 BIC 准则中模型阶数 p p p 的 增加对 BIC 值的影响较大, 所以 BIC 准则确定的实用模型的阶数将低于 AIC 准则确定的阶数. 可以证明, BIC 准则确定的模型阶数是其真值的一致估计.

事实上, 定义不同的准则函数, 是为了对拟合残差与参数个数之间进行不同的权衡, 以体现使用者在模型拟合误差与模型复杂程度之间的不同侧重.

程序源代码

%% BIC 准则定阶
maxLags = 8;
BIC = zeros(maxLags,1);
for j=1:maxLags
    mdl = ar(smooth_data,j);
    BIC(j) = mdl.Report.Fit.BIC;
end
% 画热度图来表示 BIC 数值的分布
figure(5)
heatmap(BIC/1000);
xlabel("BIC")
ylabel("AR Lags")
OptimalARLags_BIC = find(BIC==min(BIC));
title('Optimal AR ')

BIC 准则下的最优 AR 模型的阶数为 2 阶.

参数估计

通过以上分析可知, BIC 准则下的最优 AR 模型的阶数为 2 阶. 于是考虑建立 AR(2) 模型.

程序源代码

%%  参数估计
disp("建立的 AR 模型如下")
mdl = ar(smooth_data,OptimalARLags_BIC)
a = zeros(length(mdl.Report.Parameters.ParVector),1);
a(1:length(mdl.Report.Parameters.ParVector)) = -mdl.Report.Parameters.ParVector;

命令行窗口输出

建立的 AR 模型如下

mdl =
Discrete-time AR model: A(z)y(t) = e(t)
  A(z) = 1 - 0.6436 z^-1 - 0.2325 z^-2 
                                       
采样时间: 1 seconds
  
Parameterization:
   Polynomial orders:   na=2
   Number of free coefficients: 2
   Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.

Status:                                                         
Estimated using AR ('fb/now') on time domain data "smooth_data".
Fit to estimation data: 30.82%                                  
FPE: 3.296e+07, MSE: 3.259e+07

残差的白噪声检验

程序源代码

%% 残差的白噪声检验
epsilon = zeros(length(TrainData)-OptimalARLags_BIC,1);
x_hat = zeros(length(TrainData)-OptimalARLags_BIC,1);
for j =OptimalARLags_BIC+1:length(TrainData)
    x_hat(j) = smooth_data(j-OptimalARLags_BIC:j-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
    epsilon(j) =  smooth_data(j) - x_hat(j);
end
var_epsilon = var(epsilon);
mean_epsilon=mean(epsilon);
figure(6)
subplot(1,2,1)
qqplot((epsilon-mean_epsilon)/sqrt(var_epsilon))
x = -4:.05:4;
[f,xi] = ksdensity((epsilon-mean_epsilon)/sqrt(var_epsilon));
subplot(1,2,2)
plot(xi,f,'k','LineWidth',2);
hold on
plot(x,normpdf(x),'r--','LineWidth',2);
legend('标准化残差','标准正态')
hold off
figure(7)
subplot(2,1,1)
plot((epsilon-mean_epsilon)/sqrt(var_epsilon));
title('标准化残差的时序图')
subplot(2,1,2)
autocorr((epsilon-mean_epsilon)/sqrt(var_epsilon))
title('标准化残差的自相关图像')
disp('检查残差是否存在相关性')
[hLBQ,pLBQ] = lbqtest(epsilon);
disp('检验结果如下')
hLBQ,pLBQ

命令行窗口输出

检查残差是否存在相关性
检验结果如下

hLBQ =

  logical

   0


pLBQ =

    0.1111

输出变量说明

hLBQ 表示测试的结果

hLBQ = 1 表示拒绝数据无自相关的零假设而选择备择假设.(非白噪声序列)

hLBQ = 0 表示接受数据无自相关的零假设.(白噪声序列)

pLBQ 表示 lb 检验统计量的概率 p 值.

可以看到此时 hLBQ = 0, 于是可判定残差不具有相关性, 因此模型可以信任.

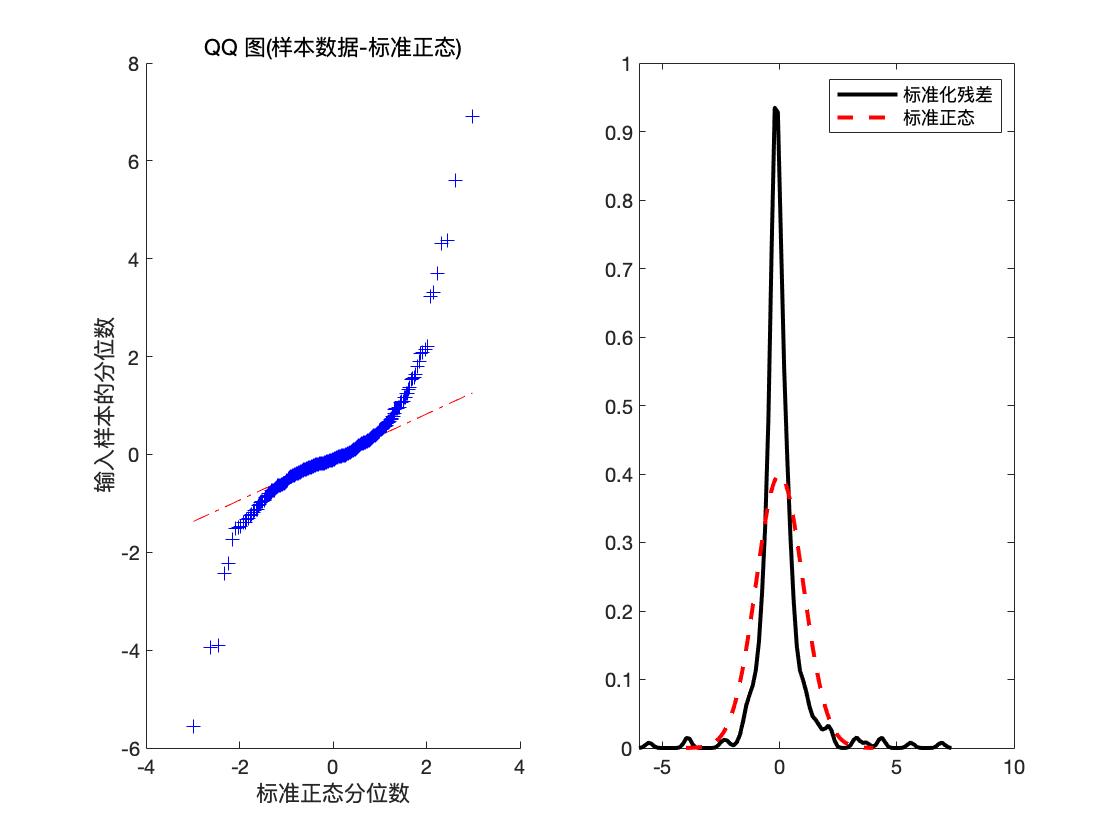
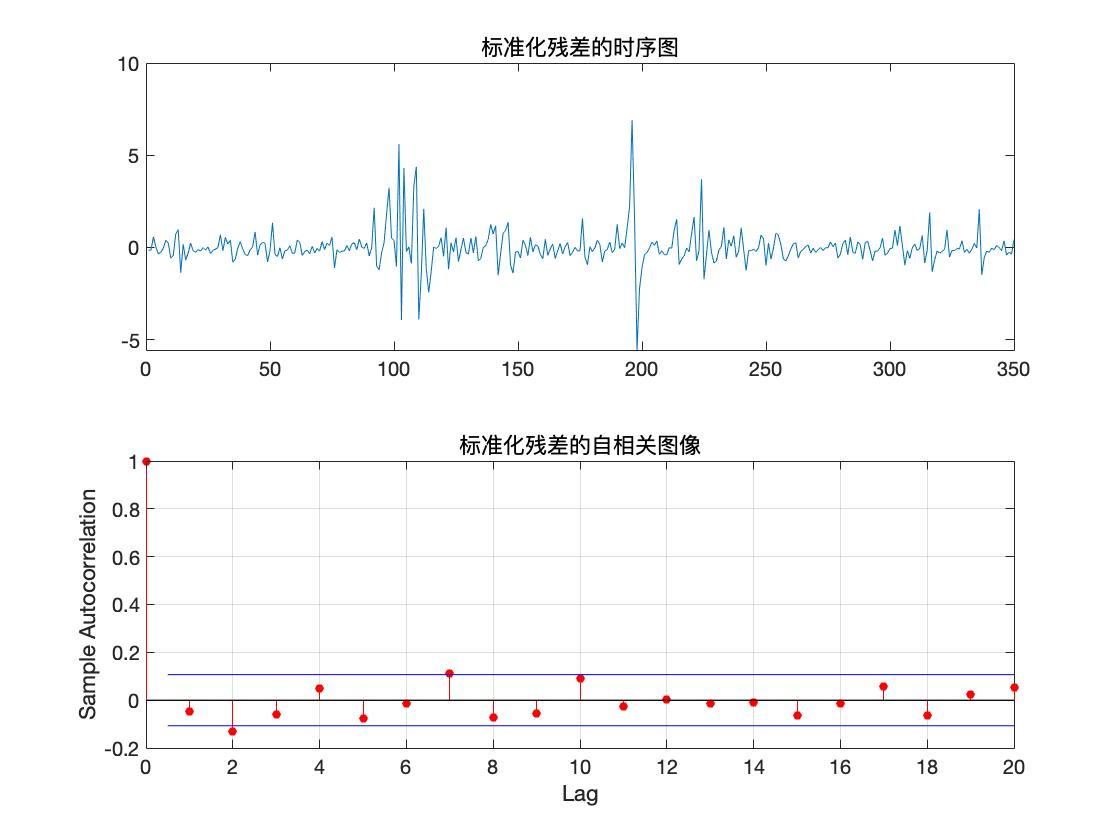
预测

我们利用建好的模型进行最佳线性预测,预测训练集后的数据,并画出预测数据的 95 % 95\\% 95% 置信区间.

X t + k X_t+k Xt+k​ 的最佳线性预测可表示为
X ^ t ( k ) = L ( X t + k ∣ X t ) = ∑ j = 1 p a j X t + 1 − j k = 1 ∑ j = 1 k − 1 a j X ^ t ( k − j ) + ∑ j = k p a j X t + k − j , 1 < k ⩽ p ∑ j = 1 p a j X ^ t ( k − j ) , k > p \\beginaligned \\hatX_t(k) &=L\\left(X_t+k \\mid \\boldsymbolX_t\\right) \\\\ &= \\begincases\\sum_j=1^p a_j X_t+1-j& k=1 & \\\\ \\sum_j=1^k-1 a_j \\hatX_t(k-j)+\\sum_j=k^p a_j X_t+k-j, & 1<k \\leqslant p \\\\ \\sum_j=1^p a_j \\hatX_t(k-j), & k>p\\endcases \\endaligned X^t​(k)​=L(Xt+k​∣

 第二步：数据归一化，将数据进行简单归一化处理，将数据归一到同一量纲上，有利于提高精度。主要用到MATLAB中mapminmax函数，实现函数如下：

第三步：经过归一化之后，就可以设置SVR的基本参数了，主要有两个参数需要设置，分别是惩罚系数c和核函数宽度g。其他基本参数如下：
options:可用的选项即表示的涵义如下
        -s    svm类型: SVM设置类型(默认0)
             0 -- c-svc
            1 --v-svc
            2 -一类SVM
            3 -- e -svR
            4 -- v-sVR
       -t  核函数类型:核函数设置类型(默认2)
            0-线性: u'v
            1 -多项式:(r*u 'v + coef0)^degree
            2- RBF函数: exp(-r|u-v|^2)
            3 -sigmoid: tanh(r*u'v + coef0)
      -d degree:核函数中的degree设置(针对多项式核函数)(默认3)
      -g r(gama):核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数)(默认1/ k)-r coefe:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认e)
      -c cost:设置c-svc. e -SVR和v-SVR的参数(损失函数)(默认1)
      -n nu:设置v-Svc，一类SVM和v- SVR的参数(默认0.5)
      -p p:设置e -sVR中损失函数p的值(默认0.1)
      -m cachesize:设置cache内存大小，以MB为单位(默认4日)-e eps:设置允许的终止判据(默认e.ee1)
      -h shrinking:是否使用启发式,0或1(默认1)
      -wi weight:设置第几类的参数c为weight*c(c-svc中的C)(默认1)-v n: n-fold交互检验模式,n为fold的个数，必须大于等于2
    其中-g选项中的k是指输入数据中的属性数。option -v随机地将数据剖分为n部分并计算交互检验准确度和均方根误差。

在设置所有的参数之后，开始对SVR进行训练，训练函数为svmtrain（），使用格式如下图：

第四步：模型建立好了之后就可以对我们的测试集进行预测。主要通过函数svmpredict（）进行预测，使用格式如下：（在这里很多人就会一个疑问，为什么预测的时候要把测试集的输出值也带进去预测呢？其实带测试集的输出值进入主要是为了计算误差error，在预测的时候没有用到测试集的输出值）最后对我们预测出来的值进行一次反归一化就得到我们预测出来的真实值了

第五步：计算相关的误差，如RMSE、MSE、R^2等 

最后代码的运行结果如下：

需要代码的同学，可以私聊我拿代码！免费

以上是关于AR 预测模型的 Matlab 实现（超详细建模流程）的主要内容，如果未能解决你的问题，请参考以下文章

支持向量机回归预测SVR——MATLAB超详细代码实现过程

matlab中的AR模型短时预测交通流

数学建模基于多种预测模型进行公路流量预测matlab

机器学习之利用线性回归预测波士顿房价和可视化分析影响房价因素实战（python实现 附源码 超详细）

超详细多元线性回归模型statsmodels_ols

超详细多元线性回归模型statsmodels_ols