TCP 的自然律

Posted 2022-11-24 dog250

周一傍晚发了一则朋友圈：

放大配图，来自：How to transfer, share and send big files fast：
​
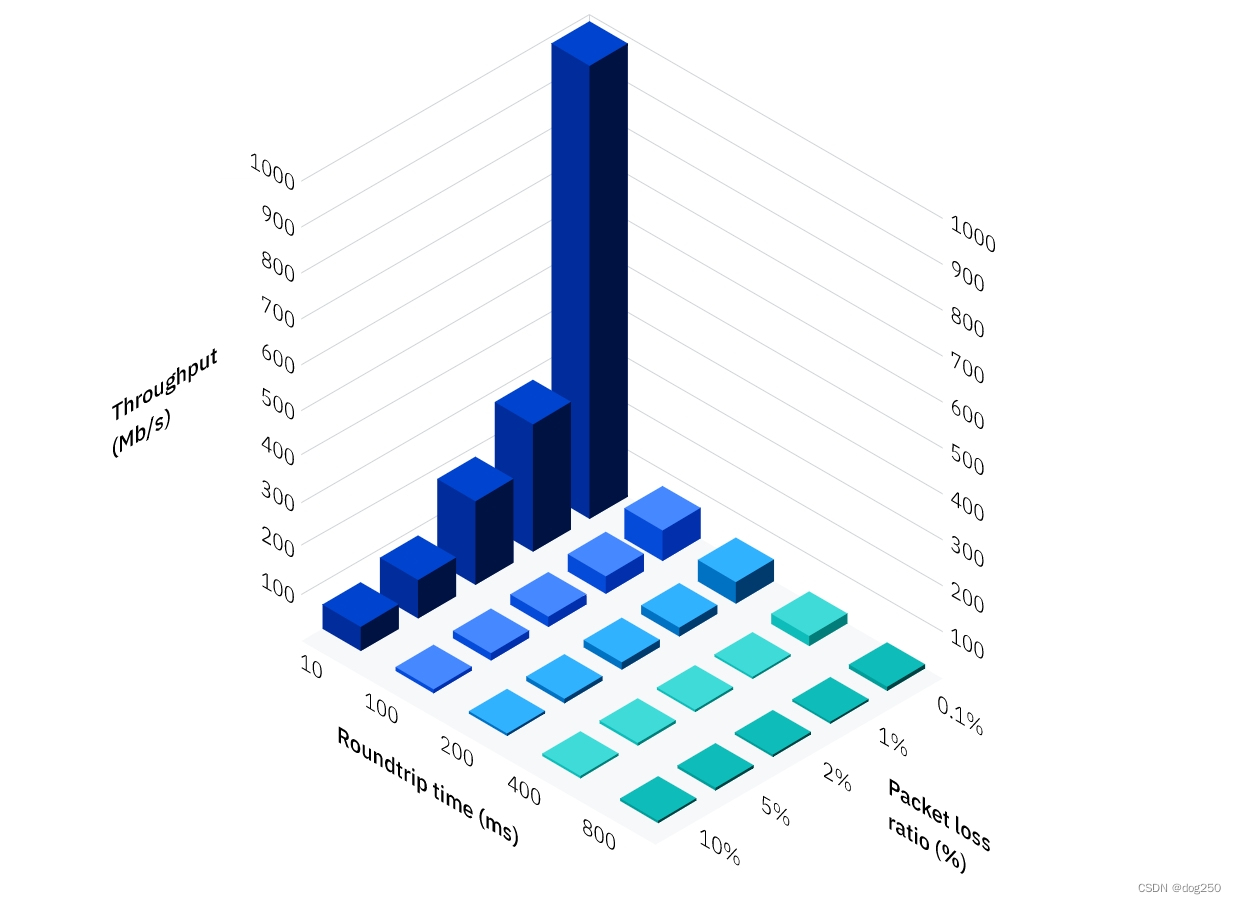
我对此事的看法：“想高效利用庞大的资源需要的代价和资源规模的增加并不是线性的，而且指数的，下凸曲线”。这个看法来自于一本书，《规模:复杂世界的简单法则》。

看来，背后还是自然律。OK，看下这个配图是如何得到的。

基于 TCP 标准 AIMD 行为，简单推导下宏观吞吐公式。以下图，设 AI 参数为 a，MD 参数为 b，丢包率为 P：

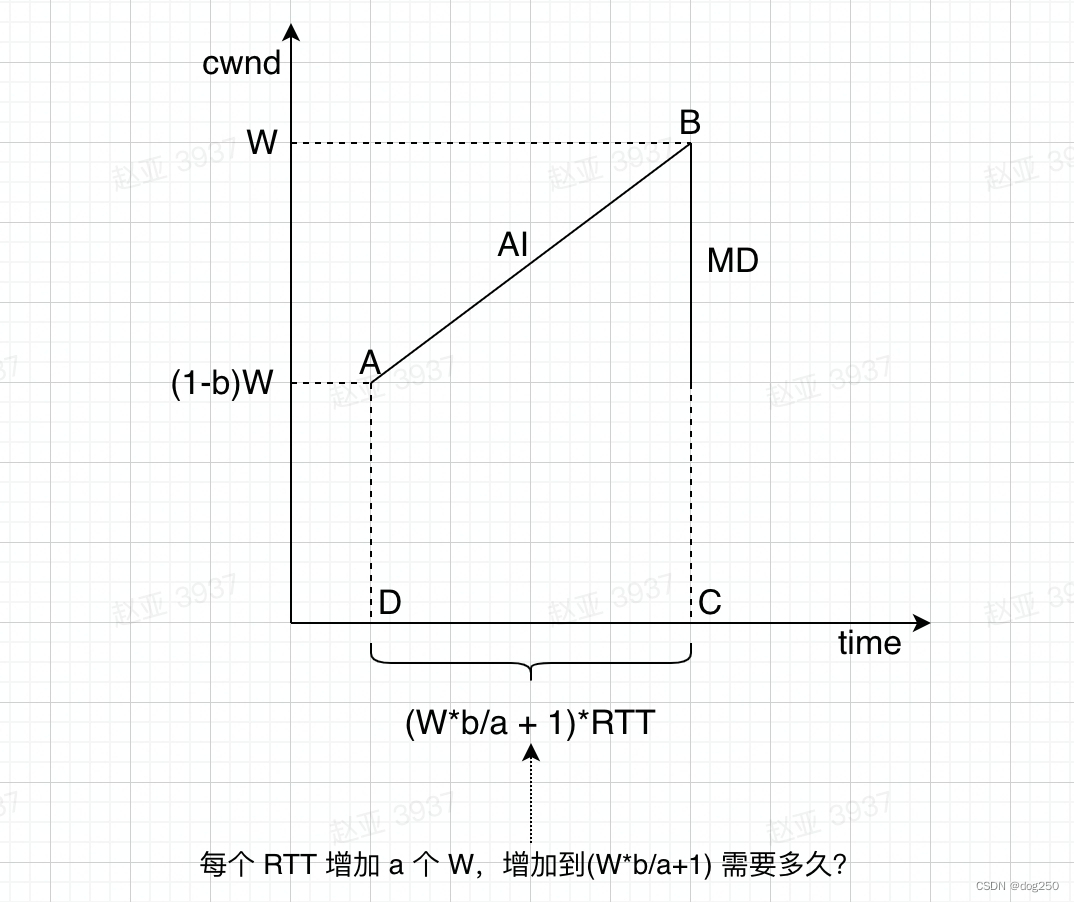
可得，一个 AIMD 周期发送总量 N：

$N=(\frac{bW}{a}+1)(1-b)W+\frac{1}{2}(\frac{bW}{a}+1)(1-b)W$

一个 AIMD 周期丢 1 个包：

$P=\frac{1}{N}$

代入 N，则：

$P=\frac{2a}{b(2-b)W^2+a(2-b)W}$

反解 W。一个忽略 W 一次项的近似解为：

$W=\sqrt{\frac{2a}{b(2-b)P}}$

求一个 AIMD 周期平均吞吐率。以 1 个 RTT 为测速区间，最小发送量为 (1-b)W，最大发送量为 W，则吞吐率 T：

$T=\frac{\frac{(1-b)W+W}{2}}{RTT}=\frac{2-b}{2\times RTT}W$

代入 W：

$T=\frac{1}{RTT}\sqrt{\frac{a(2-b)}{2b}}\frac{1}{\sqrt{P}}$

设 T，RTT， P，分别为 z，x，y，由于 a, b 均为常数，不影响形状，Geogebra 3D 画图：

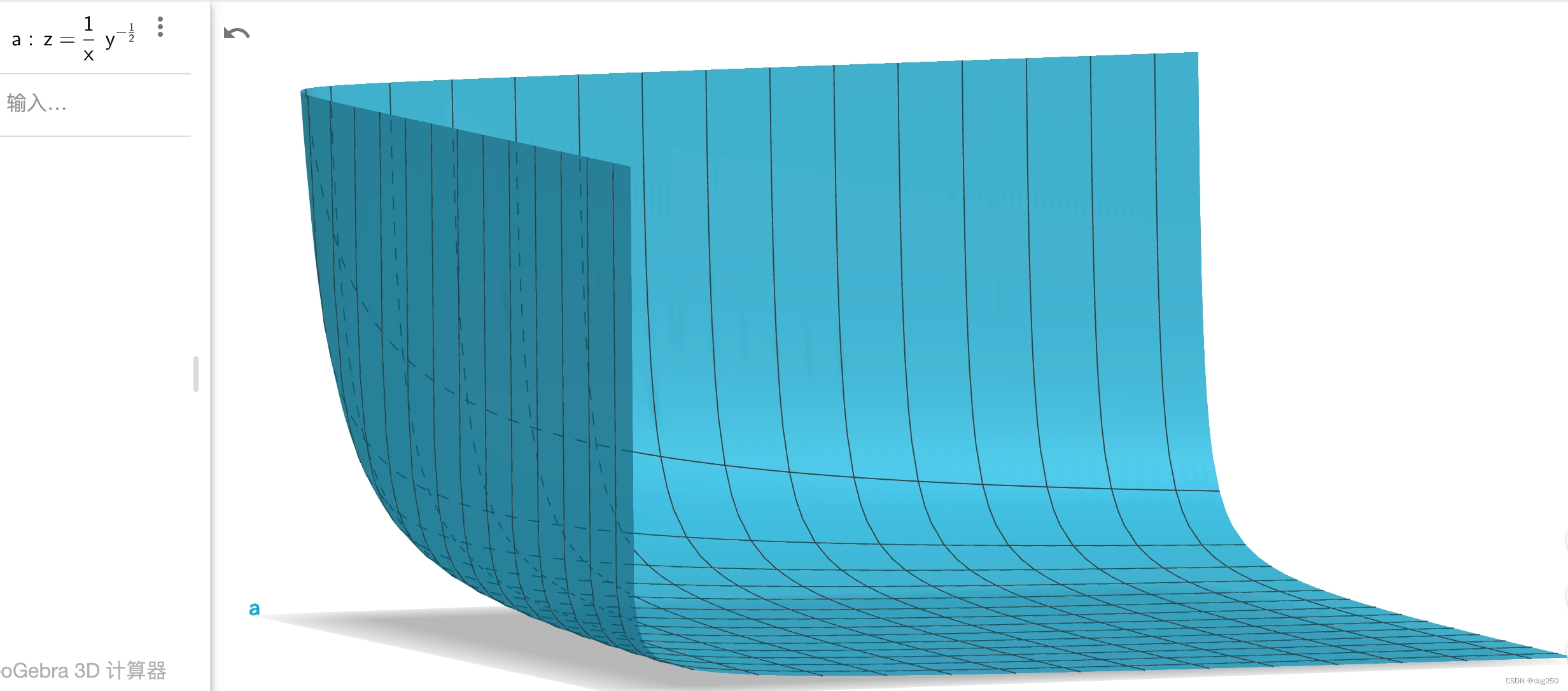
这就是朋友圈配图(离散版本)的连续版本，平滑包络线连接配图各点，与此形状一致。

以上就是 TCP 鸟样子背后自然规律的数学推导。如何理解这个规律呢？

能举起自身重量 300 倍的蚂蚁变成经理这么大也和经理一个鸟样，这个例子说过很多次。换个别的，同样来自《规模》。

增加暖气片数量带来的制暖效率的增速远慢于需要加热的空间体积，因为暖气片是二维的，空间是三维的。

换算到 AIMD TCP，吞吐增加所带来带宽利用率的增速远慢于 BDP 的增加。因为无论 RTT 增加还是丢包率增加，其作用都在 BDP 二维管道内延伸，而 AIMD TCP 吞吐的依据则仅来自于 ACK 信号，换句话说，AIMD 只需要 ACK，不需要时间。

一维量的增速远慢于二维量的增速。这是核心。

把时间和丢包维度考虑进来，就是 BBR 带宽利用率高的原因：

• BBR 不在对 ACK 到达进行反应，二是对 packet round 内的速率进行反应。
• 为对抗丢包，BBR 同样引入时间鲁棒性，坚持丢包前速率，取代立即反应。
• 为弥补丢包损失，BBR 以 25% 增益补损，BBR 竟能忍受高达 20% 丢包率。

理想中的 BBR Throughput/Rrr/Loss 是(来自：https://www.ibm.com/cloud/smartpapers/aspera/transfer-large-files/)：

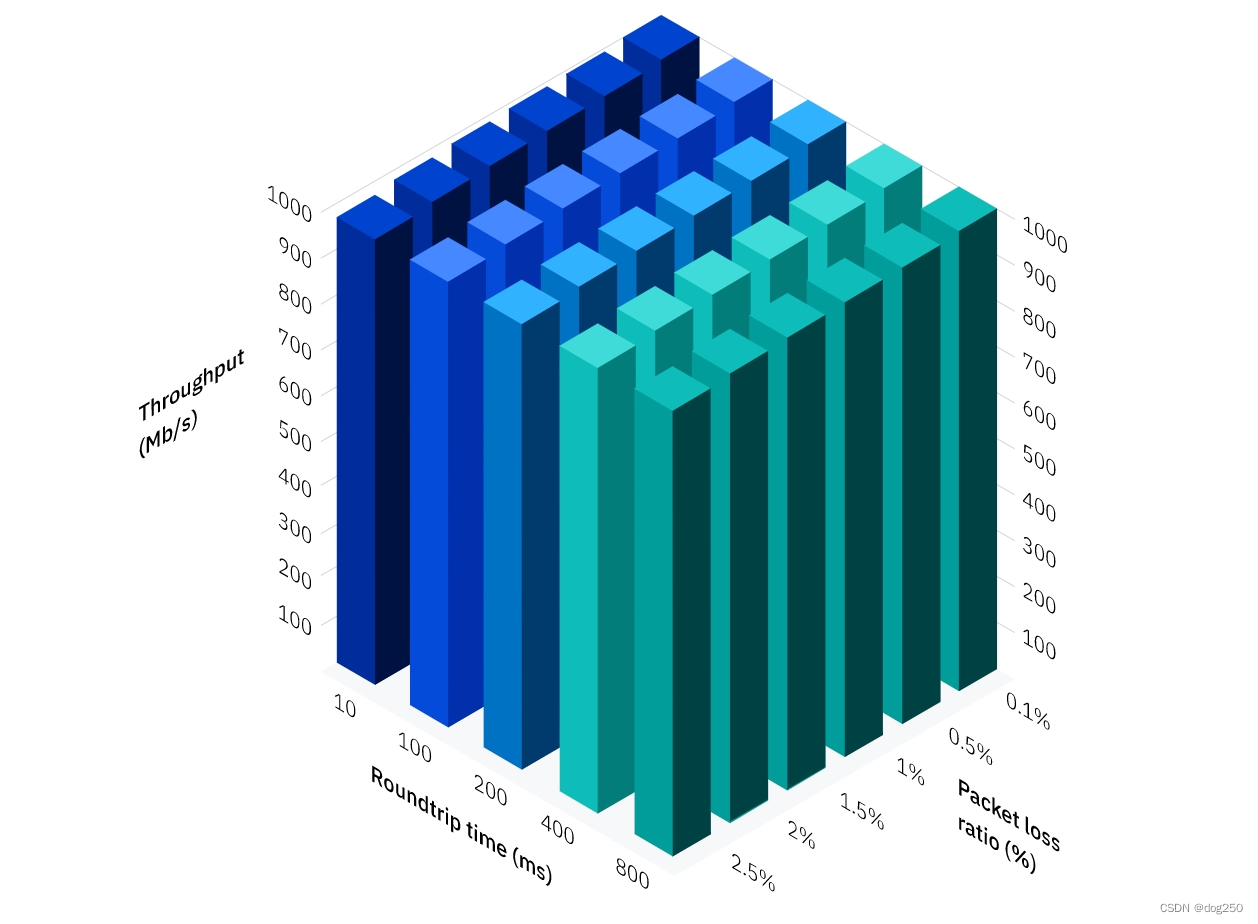
现实中 BBR 据此非常遥远。也许是 TCP 固有缺陷导致，也许是别的。

经常有人问，40% 的增益是否能容忍 40% Loss，非常不对。TCP 端到端的本质使它无法识别 Loss 过程，40% 增益意味着 BBR 以 140% 的速率发送，这个增益将放大 MIMD。

无论怎样，BBR 仍保留了无视现实的假设。如多流场景下，当 buffer 开始 bloat，只要 probe 都会带来 delivery rate 增益，并不存在 BBR 假设的 btlBW*RTprop 上界的约束。

准备写个朴素的 tcp_caohejing 算法，实现一个新思路。但下回分解。

居家办公，省掉了通勤时间，吃完晚饭出去探视了家附近的烂尾楼，唏嘘。归家继续思考漕河泾算法，作为前奏把周一傍晚朋友圈里的配图解释一下。本文除了漕河泾算法的引，也算一本极佳的书《规模》的读后感。

浙江温州皮鞋湿，下雨进水不会胖。