2019 第十届蓝桥杯省赛A组题解
Posted 爱编程的鱼
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2019 第十届蓝桥杯省赛A组题解相关的知识,希望对你有一定的参考价值。
本次试题难度(对专业算法竞赛选手来说)不大,但是考验基本的编程基本功和数学思维。估计完成80%即可获得省一进入决赛(根据一些公开的反馈,如果有准确数据请告诉我),因此更多的是需要细心。
至于C/C++还是Java我觉得不重要,因为题目除了顺序有点不同,内容是一样的。而且核心在于算法。

答案:2658417853
送分题。两重循环,大循环从 1 到 2019,小循环一依次剥离每一位(一直 % 10 后整除 10),进行判断,然后求和。
本题作为送分题,非常贴心加了一句最下面的一段话,差点就等同于“你给我用上 long long 啊”。如果不提示这句话,而且结果还是正的,不知道有多少选手会掉进陷阱。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
ll ans = 0;
int is_2019(int x)
while (x)
int t = x % 10;
if (t == 2 || t == 0 || t == 1 || t == 9)
return 1;
x /= 10;
return 0;
int main()
for (int i = 1; i <= 2019; i++)
if (is_2019(i)) ans += i * i;
cout << ans <<endl;
return 0;

答案:4659
类似于斐波那契数列。由于数据范围才是 2×107 ,完全可以暴力一重 O(n) 的复杂度循环解决,可以开数组记录 f[1],f[2]...f[20190324],注意每次加后要 mod 10000。也可以使用循环变量只记录计算到的前面三项节约内存空间。
其实对于这种题目,即使数据范围到 int ( 2×109 ),也是可以这么做,因为你可以挂机让电脑运算,跑个几分钟还是可以跑出来的。
但是,如果数据范围再大一些,就要用矩阵快速幂加速递推式了,不过也不算难。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
int main()
int a, b, c, d;
a = b = 1;
c = 3;
for(int i = 4; i < 20190324; i++)
d = (a + b + c) % 10000;
a = b;
b = c;
c = d;
cout << d << endl;
return 0;

答案:34
证明:
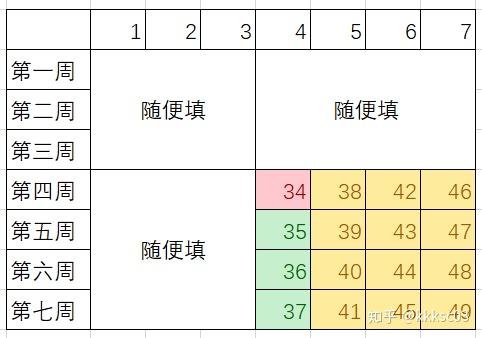
为了方便理解,假设每一周都是递增,且每一周的中位数都是递增。
要找中位数的中位数,那么必须红色区域(要求的)要小于绿色区域。而每行的绿色区域要小于同一行的黄色区域。因为红色区域是在这 16 个格子中最小的一个,根据贪心策略,答案就是 49-16+1。同时,剩下的部分就可以随便写了,不会影响到这个结果。

下面的具体数字略。
答案:DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
求最短迷宫问题是广度优先搜索的入门题,所以直接进行广度优先搜索就是了。使用一个队列,将入口位置放入队首。
当队伍非空,或者找到答案时,循环截止。每次从队首出队,分别从 下、上、左、右 进行扩展,注意要使用 vis 数组记录是否已经访问过了,还要记录更新结点遇到的方向。
代码:
#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
const int n = 30, m = 50;
int delta[4][2] = 1, 0, 0, -1, 0, 1, -1, 0;
int way[n + 5][m + 5], map[n + 5][m + 5], vis[n + 5][m + 5];
char cc[5] = "DLRU";
char ans[n * m + 5];
struct node
int x, y;
;
int main()
freopen("maze.txt", "r", stdin);
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
char a = ' ';
while(a != '1' && a != '0')cin >> a;
map[i][j] = a == '1' ? 1 : 0;
queue<node> q;
node tmp = 0, 0;
q.push(tmp);
vis[0][0] = 1;
while(!q.empty())
node now = q.front();
q.pop();
for(int k = 0; k < 4; k++)
int x = now.x + delta[k][0], y = now.y + delta[k][1];
if(x < 0 || y < 0 || x >= n || y >= m
|| vis[x][y] || map[x][y])
continue;
vis[x][y] = 1, way[x][y] = k;
node tmp = x, y;
q.push(tmp);
int x = n - 1, y = m - 1, num = 0;
while(x != 0 || y != 0)
int k = way[x][y];
ans[num++] = cc[k];
x -= delta[k][0], y -= delta[k][1];
num--;
do
cout << ans[num];
while(num--);
return 0;

答案:579706994112328949
最大的问题是理解题意……不过理解了的话,也需要了解一些数论知识。
首先需要暴力质因数破解 p 和 q(枚举奇数到 n ),n 是 19 位,所以 p 不会超过 9 位,即使枚举也是可以接受的。可以得到 p=891234941 q=1123984201。
现在已知 d,还要求 e,考虑到 d 和 m=(p-1)(q-1) 互质,所以 d×e≡1(modm) 。那么很自然而然的想出求出 d 关于 m 的逆元(【模板】乘法逆元 - 洛谷题库 >>)。至于不会逆元?也可以尝试直接进行枚举 e,但怕是考试结束都枚举不完。
经提示,问题也等价于 d×e=k×m+1 找到一个 k(从 1 枚举),使得 k×m≡d−1(modd) ,实际上 k 只需要枚举到 d-1,考虑到 d 大约为 2e5,复杂度可以接受。
获得 e 之后,就直接按照公式求乘积,这里得使用快速幂加速。由于一般的快速幂可能爆 long long,需要加个快速乘规避(龟速乘也可以就是有点慢)。
本题思路很显然,几乎没什么思维难度(前提是会使用一些数学工具)。不过写的时候可能会掉进溢出的坑(我对着一个负数看了很久)。对于ACM区域赛/OI省选级别竞赛选手来说这个算基本功,但是如果没有专业训练的同学,还是考虑放弃。
如果是可以用 Python 或者 Java,那么大概就没那么多溢出的屁事了。
代码:
#include <iostream>
using namespace std;
typedef long long ll; // 懒得写那么多 long long
void Exgcd(ll a, ll b, ll &x, ll &y) // 扩展欧几里得求逆元
if(!b) x = 1, y = 0;
else Exgcd(b, a % b, y, x), y -= a / b * x;
inline ll mul(ll x, ll y, ll p) // 快速乘,防止爆 long long
ll z = (long double)x / p * y;
ll res = (unsigned long long)x * y - (unsigned long long)z * p;
return (res + p) % p;
ll fpm(ll x, ll power, ll p) // 快速幂
x %= p;
ll ans = 1;
for(; power; power >>= 1, x = mul(x, x, p))
if(power & 1)(ans = mul(ans, x, p)) %= p;
return ans;
int main()
ll n = 1001733993063167141, d = 212353, p, q;
for(ll i = 3; i * i < n; i += 2)
/*
if(i % 1000000000 == 1) // 进度条,要不然不知道程序有没有再跑
cout << i << endl;
*/
if(n % i == 0) //n % i== 0
p = i;
q = n / i;
break;
cout << "p = " << p << endl;
cout << "q = " << q << endl;
/*
p = 891234941;
q = 1123984201;
*/
ll e, m = (p - 1) * (q - 1), x, y;
Exgcd(d, m, x, y);
e = (x % m + m) % m;
ll C = 20190324;
// cout << mul(d, e, m); 验证 d*e mod m = 1
cout << fpm(C, e, n) << endl;
return 0;
解析:
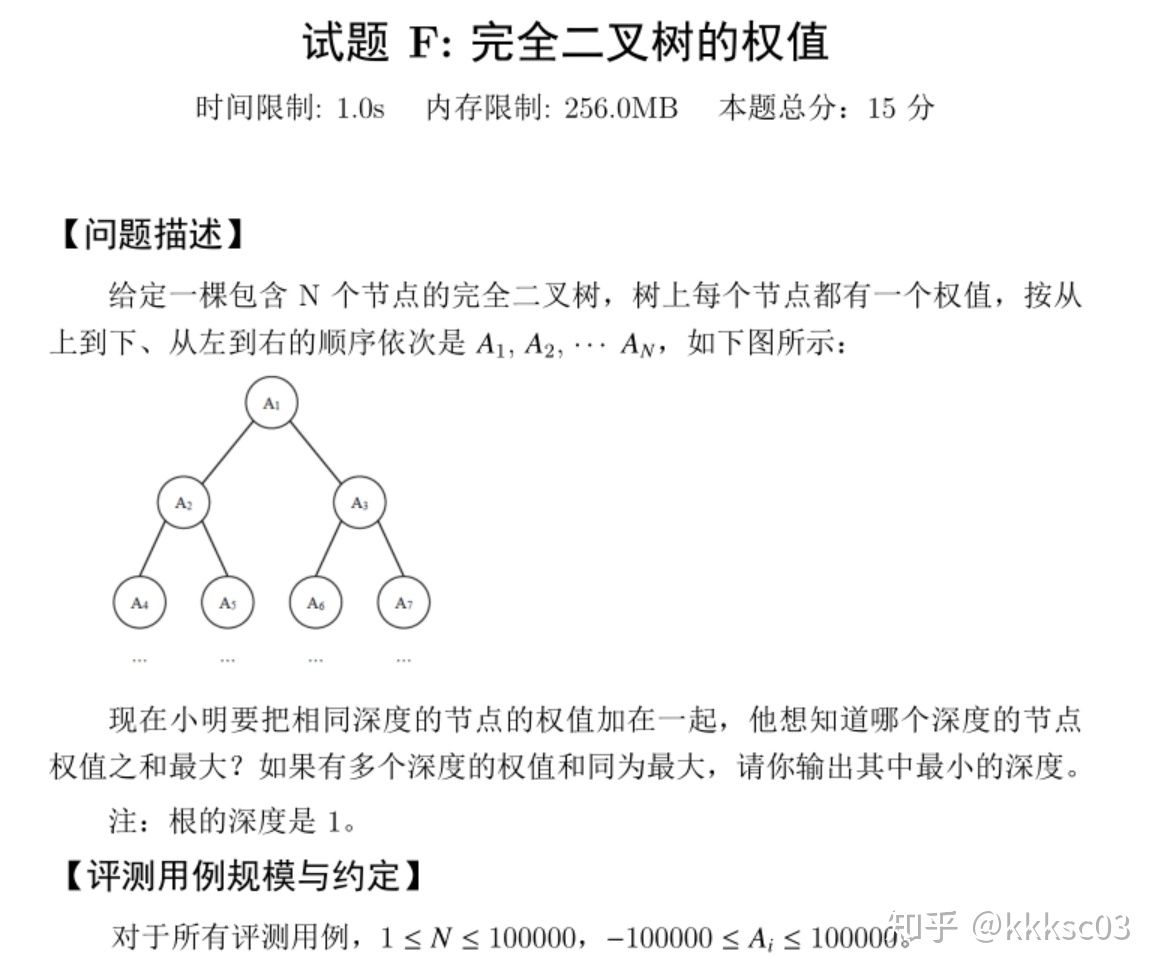
首先需要了解什么是完全二叉树。

二叉树定义,节选自《深基》
因此,存储一个完全二叉树,可以使用一维数组存下所有结点。从上到下,从左到右,编号依次增加。可以发现,第一层有 1 个结点,第二层有 2 个,第三层有 4 个,第四层有 8 个……第 i 层有 2i−1 个结点。还可以发现,结点编号为 i 的话,它的左右子节点的编号分别是 2×i 和 2×i+1,不过这个和本题无关。
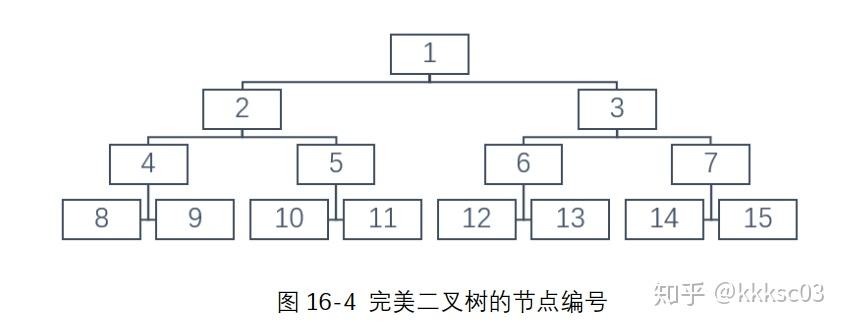
由于我们知道每一层的节点个数,可以直接输入数据后按层统计,甚至都可以不用数组把这些数字存下来。只要记录好读入的数字个数,在合适的时间退出循环就行。注意 << 符号是左移,1<<layer 的意思就是 2layer 。如果读到的数字到了 n,那么就可以跳出循环,使用变量 flag 进行标记和判断。
本题有两个需要注意的地方
- 数据可能有小于 0 的,导致每层总和可能小于 0。
- 最多的一层可能有 100000-2^16 大约是 35000 个结点,所以要用 long long 防止总合爆 int。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
int main()
long long n, maxnum = -3500000000ll, maxlayer, cnt = 0, flag = 0;
cin >> n;
for(int layer = 0; ; layer++) // 枚举每一层,习惯上从 0 开始
long long sum = 0, a;
//cout << "<<" << (1 << layer) << endl;
for(int i = 0; i < (1 << layer); i++) // 每一层的结点个数
cin >> a;
sum += a;
if(++cnt >= n)
flag = 1;
break;
//cout << sum << endl;
if(sum > maxnum)
maxnum = sum, maxlayer = layer + 1;
if(flag) break;
cout << maxlayer;
return 0;

解析:
最朴素的方法是枚举每一秒,然后枚举每个店铺是否有新的订单,然后进行增减操作,不过这个算法复杂度显然不行。
考虑到每一个店铺之间互相独立,所以可以依次判断每个店铺最后是否在优先缓存中。因此,只需要建立 N 个 vector,每个 vector 都可以存储这家店铺的订单时间。
然后从最开始的订单进行处理,判断上一个订单到现在过去了多久(要记录上一个订单的时间,和上一个订单处理后的优先级,初始值都是 0)。如果上一个订单处理的优先级减去经过的时间(注意要减一,因为这个时候有新订单,不用再减了),如果小于 0 则变为 0,然后加上 2。注意同一时间有多个订单的情况。
最后我们就可以计算得到这个店铺时刻 T 的优先值,也要根据最后一个订单的经过时间来计算。
如果优先值大于 5 那显然在缓存中。如果优先值小于等于 3 则显然不在缓存中。那 4 和 5 呢?如果是 6 降到 4/5 那么可以算,否则不算(注意优先值不可能连续保持不变)。所以可以进行以下讨论:
秒 1 2 3 4 5
值 3 5 (不符合情况)
值 6 5 (符合情况)
值 6 5 4 (符合情况)
值 3 5 4 (不符合情况)
值 2 4 (不符合情况)可以发现,当最后优先级为 5 的时候,最后一秒不能有订单;优先级为 4 的时候,最后一秒和倒数第二秒都不能有订单。所以在最后判断一下是否出现这种情况就可以了。排序复杂度O(MlogM) ,处理订单复杂度 O(M+N)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector <int> q[100005];
int N, M, T, ans = 0;
int main()
cin >> N >> M >> T;
while(M--)
int ts, id;
cin >> ts >> id;
q[id].push_back(ts);
for(int i = 1; i <= N; i++)
sort(q[i].begin(), q[i].end());
int last_time = 0, priority = 0, ts;
for(int order = 0; order < q[i].size(); order++)
ts = q[i][order];
if(ts - last_time >= 1)
priority -= (ts - last_time - 1);
priority = max(0, priority);
priority += 2;
last_time = ts;
priority -= (T - last_time);
if(priority > 3
&& (priority > 5
|| priority == 5 && ts != T
|| priority == 4 && ts < T - 1
)
) ans++;
cout << ans;
return 0;

解析:
将一系列连续的数字作为一个集合。虽然可以平衡树或者set求得集合最大值,但是显然还是并查集(【模板】并查集 >>)用起来快。
首先进行并查集初始化。然后依次读入数字。
- 如果这个没有被占用,那么这个就是答案,可以直接插入。
- 如果被占用了,则使用并查集找到这个集合,找到祖先。其下一个就是可以插入的空。考虑到并查集是单向从小指向大的,所以祖先一定是最大的。注意要使用上路径压缩
注意使用 vis 数组占用掉。然后需要依次判断这个占坑后,是否和前面一段集合和后面一个集合连在一起,如果是的话就将前面一个的祖先改掉。当然,数字 1 没有前一个。
有一个问题需要明确,如果一直插入 1000000,那么到最后的数字会超出 1000000,因此并查集的值域需要开到 max(A_i)+N。
代码:
#include <cstdio>
#include <iostream>
using namespace std;
#define MAXN 100005
#define MAXA 1100005
int a, N, fa[MAXA], vis[MAXA];
int get_father(int x) // 查找祖宗
if (x == fa[x]) return x;
return fa[x] = get_father(fa[x]);
int main()
cin >> N;
for (int i = 1; i < MAXA; i++)
fa[i] = i; // 并查集初始化
for (int i = 0; i < N; i++)
cin >> a;
int ans = vis[a] ? get_father(a) + 1 : a;
cout << ans << ' ';
vis[ans] = 1;
if (ans != 1 && vis[ans - 1])
fa[ans - 1] = ans;
if (vis[ans + 1])
fa[ans] = ans + 1;
return 0;

解析:
非常基础的状态压缩动态规划,因为数据范围非常小。可以使用二进制中的每一位表示某袋中是否有这某种糖果。例如一共有 5 种糖果,其中一袋是 [1,2,3],那么对应的二进制是 [00111]=7(注意二进制是右边是低位,左边是高位);如果是 [1,1,3]那么对应二进制是 [00101]=5。可以使用或运算符号来表示糖果的集合合并,用做左移符号(<<)来移动每一位。
接下来,设 f[S] 为达成 S 集合需要的最少糖果袋数,初始值都设为正无限,f[0]=0。
开始处理每一袋糖果,然后枚举每一种糖果集合的状态,如果f[S]是正无限,说明这种状态暂时不可达,暂时跳过。对于可行的状态,尝试把这一袋糖果加入到集合中,对,还是使用或运算。例如原来的集合是 [10101]=21,要加上状态为 [01110]=14 的糖果,其结果就是 [10101]∪[01110]=21|14=31。注意要在原基础上增加 1(因为新买了一包)。注意别覆盖之前出来的更好的结果,所以要取最小值。
最后输出全1的集合对应的数量,注意特别判断无解的状态。
代码:
#include <cstring>
#include <iostream>
using namespace std;
#define MAXN 105
int N, M, K, tmp;
int f[1 << 20], a[MAXN];
int main()
cin >> N >> M >> K;
for (int i = 0; i < N; i++)
for (int j = 0; j < K; j++)
cin >> tmp;
a[i] |= 1 << tmp - 1; // 加入糖果构造集合
memset(f, 127, sizeof(f));
f[0] = 0;
for (int i = 0; i < N; i++)
for (int S = 0; S < 1 << M; S++) // 枚举所有状态
if (f[S] > MAXN)continue;
f[S | a[i]] = min(f[S | a[i]], f[S] + 1);
cout << (f[(1 << M) - 1] < MAXN ? f[(1 << M) - 1] : -1) << endl;
return 0;
蓝桥杯省赛C++组别大学B组历年题解
以上是关于2019 第十届蓝桥杯省赛A组题解的主要内容,如果未能解决你的问题,请参考以下文章