:图形分析
Posted Sonhhxg_柒
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了:图形分析相关的知识,希望对你有一定的参考价值。
🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
文章目录
图形分析是一种数据分析技术,用于确定图形中对象之间关系的强度和方向。图形是用于对对象之间的关系和过程进行建模的数学结构。它们可用于表示数据中的复杂关系和依赖项。图形由表示系统中实体的顶点或节点组成。这些顶点由表示这些实体之间关系的边连接。
图形简介
它可能不会立即显现出来,但图表无处不在。LinkedIn,脸书和推特等社交网络是图表。互联网和万维网是图形。计算机网络是图形。自来水管道是图形。道路网络是图形。GraphX等图形处理框架具有专门用于处理面向图形的数据的图形算法和运算符。
无向图
无向图是具有没有方向的边的图。无向图中的边可以在两个方向上遍历,并表示双向关系。图 6-1 显示了一个具有三个节点和三个边的无向图。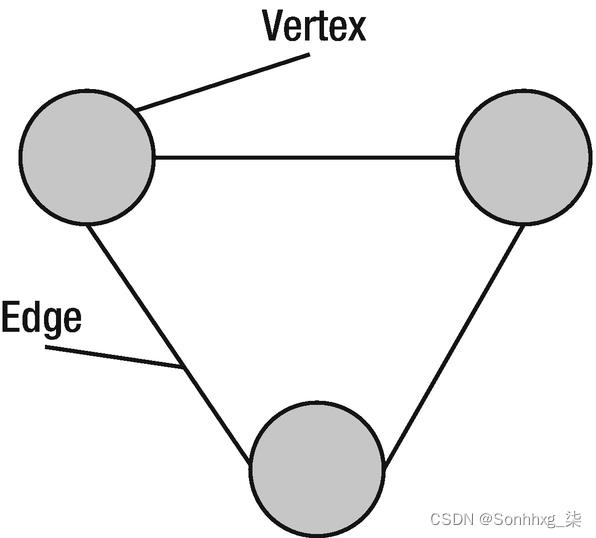
图6-1无向图
有向图
有向图具有指示单向关系的方向的边。在有向图中,每条边只能沿一个方向遍历(图 6-2)。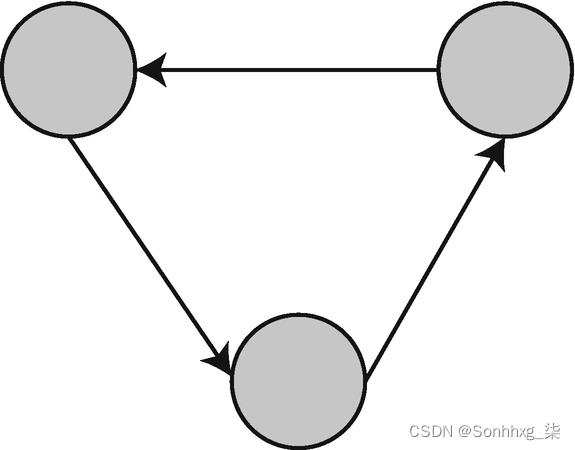
图6-2 有向图
定向多图
多图在节点之间具有多条边(图 6-3)。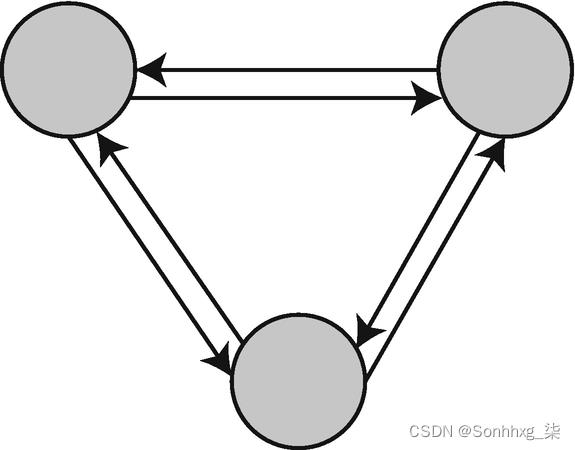
图6-3定向多图
属性图
属性图是有向多图,其中顶点和边具有用户定义的属性v(图 6-4)。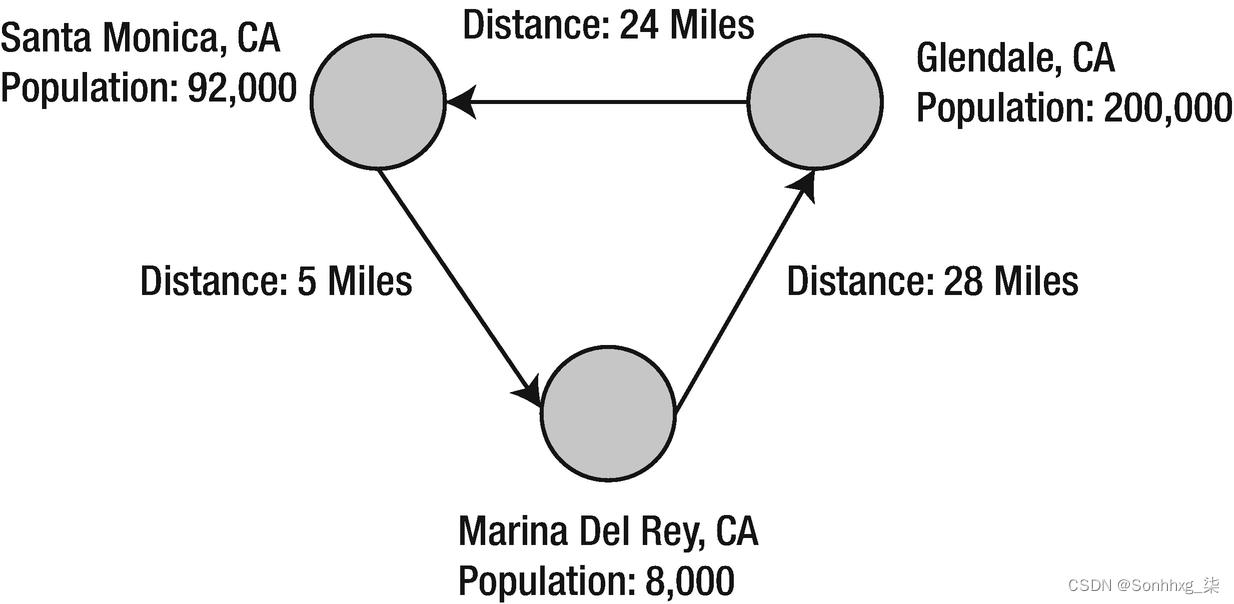
图6-4属性图
图形分析用例
图形分析在各行各业蓬勃发展。任何利用大量连接数据的项目都是图形分析的完美用例。这并不意味着是一个全面的用例列表,但它应该让您了解图形分析的可能性。
欺诈检测和反洗钱 (AML)
欺诈检测和反洗钱可能是图分析最广为人知的用例之一。手动筛选数百万笔银行交易以识别欺诈和洗钱活动即使不是不可能,也是令人生畏的。通过一系列相互关联的看似无害的交易来隐藏欺诈的复杂方法使问题更加复杂。检测和预防这些类型的攻击的传统技术在这个时代已经过时了。图形分析是这个问题的完美解决方案,它使可疑交易与其他异常行为模式联系起来变得容易。像 GraphX 这样的高性能图形处理 API 允许非常快速地从一个事务到另一个事务的复杂遍历。也许最著名的例子是巴拿马文件丑闻。通过使用图形分析识别数百万份泄露文件之间的联系,分析师能够发现知名外国领导人,政治家甚至女王拥有的离岸银行账户中的隐藏资产。
数据治理和法规遵从性
典型的大型组织将数百万个数据文件存储在中央数据存储库(如数据湖)中。这需要适当的主数据管理,这意味着每次修改文件或创建新副本时都要跟踪数据沿袭。通过跟踪数据沿袭,组织可以跟踪数据从源到目标的移动,从而了解数据从点到点的所有变化方式。合理的数据沿袭策略可增强对数据的信心,并实现准确的业务决策。数据沿袭也是维护数据相关法规遵从性的一项要求,例如《通用数据保护条例》(GDPR)。被发现违反GDPR可能意味着巨额罚款。图形分析非常适合这些用例。
风险管理
为了管理风险,对冲基金和投资银行等金融机构使用图形分析来识别相互关联的风险和模式,这些风险和模式有可能引发“黑天鹅”事件。以2008年金融危机为例,图分析本可以通过揭示抵押贷款支持证券(MBS)、抵押债务凭证(CDO)和信贷违约互换之间错综复杂的相互依赖关系,为衍生品证券化的复杂过程提供可见性。
运输
空中交通网络是一个图表。机场表示顶点,而路径表示边。商业飞行计划是使用图形分析创建的。航空公司和物流公司使用图形分析进行路线优化,以确定最安全或最快的路线。这些优化可确保安全,并节省时间和金钱。
社交
社交网络是图形分析最直观的用例。如今,几乎每个人都有一个“社交图谱”——一个代表一个人与社交网络中其他人或群体的社交关系的图。如果你在脸书,推特,脸书或LinkedIn,你有一个社交图谱。一个很好的例子是Facebook使用另一个开源图形框架Apache Giraph来处理和分析内容排名和推荐的万亿个边缘。
网络基础设施管理
互联网是互连路由器、服务器、台式机、物联网和移动设备的巨大图形。政府和企业网络可以被视为互联网的子图。即使是小型家庭网络也是图形。设备表示顶点,网络连接表示边。图形分析使网络管理员能够可视化复杂的网络拓扑,这对于监视和故障排除非常有用。这对于由数千个连接设备组成的大型企业网络尤其有价值。
GraphX简介
图X是斯帕克基于RDD的图形处理API。除了图形运算符和算法之外,GraphX 还提供用于存储图形数据的数据类型。
Graph(图)
属性图由 Graph 类的实例表示。就像RDD一样,属性图被分区并分布在执行程序中,并且可以在发生崩溃时重新创建。属性图是不可变的,这意味着必须创建新图形才能更改图形的结构或值。
VertexRDD(顶点)
属性图中的顶点由顶点 RDD 表示。每个顶点只有一个条目存储在顶点RDD中。
Edge(边缘)
Edge 类包含与源和目标顶点标识符对应的源和目标 ID,以及存储边缘属性的属性。西
EdgeRDD
属性图中的边缘由边缘RDD表示。
EdgeTriplet(边缘三重奏)
边和它所连接的两个顶点的组合由 EdgeTriplet 类的实例表示。它还包含边的属性及其连接的顶点。
EdgeContext
类公开三元组字段以及用于将消息发送到源顶点和目标顶点的函数。
GraphX示例
对于此示例(清单 6-1),我将使用 GraphX 来分析南加州不同城市之间的距离。我们将根据表 6-1 中的数据构造一个类似于图 6-5 的属性图。
表6-1南加州不同城市之间的距离
| Source | Destination | Distance |
| Santa Monica, CA | Marina Del Rey, CA | 5 Miles |
| Santa Monica, CA | Glendale, CA | 24 Miles |
| Marina Del Rey, CA | Glendale, CA | 28 Miles |
| Glendale, CA | Pasadena, CA | 9 Miles |
| Pasadena, CA | Glendale, CA | 9 Miles |
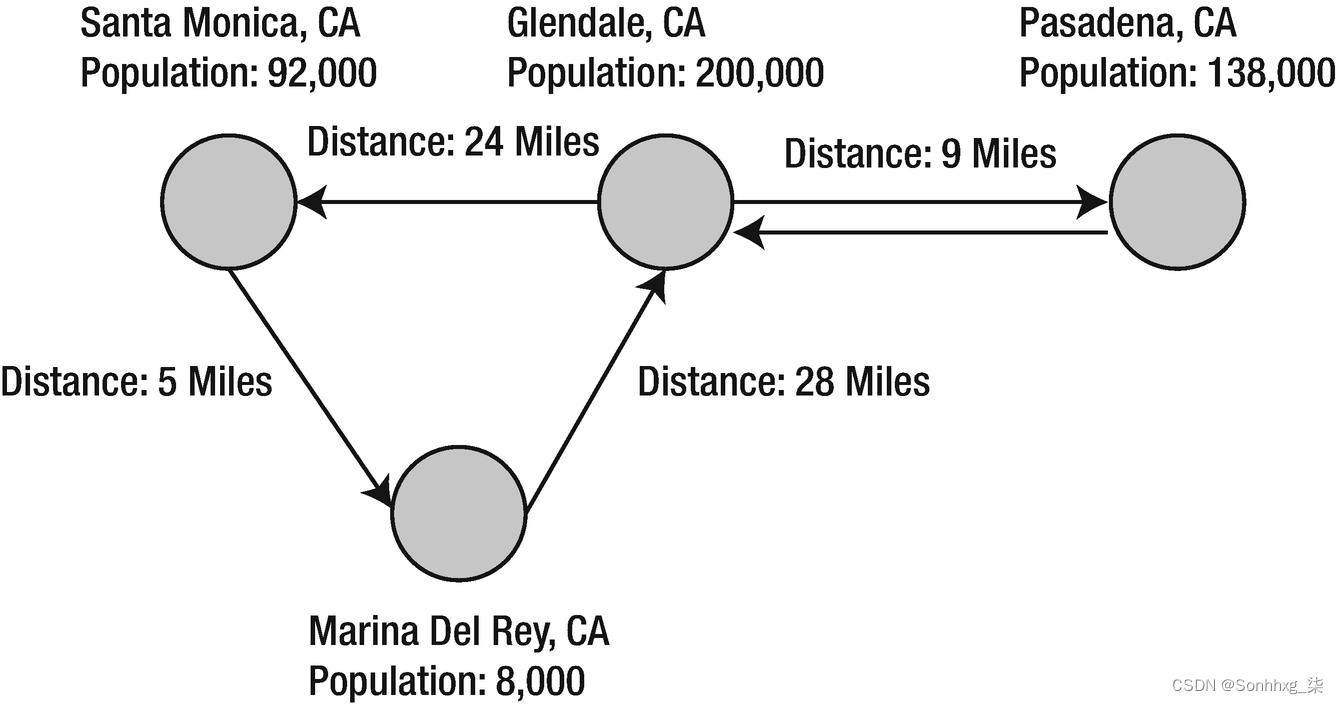
图 6-5属性图
importorg.apache.spark.rdd.RDD
importorg.apache.spark.graphx._
// 定义顶点。
val vertices = Array((1L, ("Santa Monica","CA")),(2L,("Marina Del Rey","CA")),(3L, ("Glendale","CA")),(4L, ("Pasadena","CA")))
valvRDD = sc.parallelize(vertices)
// 定义边。
val edges = Array(Edge(1L,2L,5),Edge(1L,3L,24),Edge(2L,3L,28),Edge(3L,4L,9),Edge(4L,3L,9))
val eRDD = sc.parallelize(edges)
// 创建属性图。
val graph = Graph(vRDD,eRDD)
graph.vertices.collect.foreach(println)
(3,(Glendale,CA))
(4,(Pasadena,CA))
(1,(Santa Monica,CA))
(2,(Marina Del Rey,CA))
graph.edges.collect.foreach(println)
Edge(1,2,5)
Edge(1,3,24)
Edge(2,3,28)
Edge(3,4,9)
Edge(4,3,9)
//返回顶点数。
val numCities = graph.numVertices
numCities: Long = 4
// 返回边数。
val numRoutes = graph.numEdges
numRoutes: Long = 5
// 返回每个顶点的传入边数。
graph.inDegrees.collect.foreach(println)
(3,3)
(4,1)
(2,1)
// 返回每个顶点的传出边数。
graph.outDegrees.collect.foreach(println)
(3,1)
(4,1)
(1,2)
(2,1)
// 返回所有小于 20 英里的路线。
graph.edges.filter case Edge(src, dst, prop) => prop < 20 .collect.foreach(println)
Edge(1,2,5)
Edge(3,4,9)
Edge(4,3,9)
// 类包括源属性和目标属性。
graph.triplets.collect.foreach(println)
((1,(Santa Monica,CA)),(2,(Marina Del Rey,CA)),5)
((1,(Santa Monica,CA)),(3,(Glendale,CA)),24)
((2,(Marina Del Rey,CA)),(3,(Glendale,CA)),28)
((3,(Glendale,CA)),(4,(Pasadena,CA)),9)
((4,(Pasadena,CA)),(3,(Glendale,CA)),9)
// 按最远的路线排序。
graph.triplets.sortBy(_.attr, ascending=false).collect.foreach(println)
((2,(Marina Del Rey,CA)),(3,(Glendale,CA)),28)
((1,(Santa Monica,CA)),(3,(Glendale,CA)),24)
((3,(Glendale,CA)),(4,(Pasadena,CA)),9)
((4,(Pasadena,CA)),(3,(Glendale,CA)),9)
((1,(Santa Monica,CA)),(2,(Marina Del Rey,CA)),5)
// 地图顶点将用户指定的函数应用于每个顶点。
val newGraph = graph.mapVertices((vertexID,state) => "TX")
newGraph.vertices.collect.foreach(println)
(3,TX)
(4,TX)
(1,TX)
(2,TX)
// 将用户指定的函数应用于每条边。
val newGraph = graph.mapEdges((edge) => "500")
Edge(1,2,500)
Edge(1,3,500)
Edge(2,3,500)
Edge(3,4,500)
Edge(4,3,500)Listing 6-1GraphX 示例
Graph算法
GraphX内置了几种常见图形算法的实现,例如PageRank,三角形计数和连接的组件。
PageRank(页面排名)
PageRank是一种算法,最初由谷歌开发,用于确定网页的重要性。页面排名较高的网页比页面排名较低的页面更相关。页面的页面排名取决于链接到该页面的页面的页面排名;因此,它是一种迭代算法。高质量链接的数量也有助于页面的PageRank。GraphX包括页面排名的内置实现。GraphX附带了页面排名的静态和动态版本
Dynamic PageRank(动态页面排名)
动态 PageRank 一直执行,直到排名停止更新超过指定的容差(即,直到排名收敛)。
val dynamicPageRanks = graph.pageRank(0.001).vertices
val sortedRanks = dynamicPageRanks.sortBy(_._2,ascending=false)
sortedRanks.collect.foreach(println)
(3,1.8845795504535865)
(4,1.7507334787248419)
(2,0.21430059110133595)
(1,0.15038637972023575)Static PageRank(静态页面排名)
静态页面排名执行设定的次数。
val staticPageRanks = graph.staticPageRank(10)
val sortedRanks = staticPageRanks.vertices.sortBy(_._2,ascending=false)
sortedRanks.collect.foreach(println)
(4,1.8422463479403317)
(3,1.7940036520596683)
(2,0.21375000000000008)
(1,0.15000000000000005)TriangleCount(三角形计数)
三角形由三个相连的顶点组成。三角形计数算法通过确定通过每个顶点的三角形的数量来提供聚类分析的度量。在图 6-5 中,圣莫尼卡、玛丽娜德尔瑞和格伦代尔都是三角形的一部分,而帕萨迪纳则不是。
val triangleCount = graph.triangleCount()
triangleCount.vertices.collect.foreach(println)
(3,1)
(4,0)
(1,1)
(2,1)ConnectedComponents(互联组件)
连接分量算法确定子图中每个顶点的成员资格。该算法返回子图中编号最低的顶点的顶点 ID 作为顶点的属性。图 6-6 显示了两个连接的组件。我在清单 6-2 中显示了一个示例。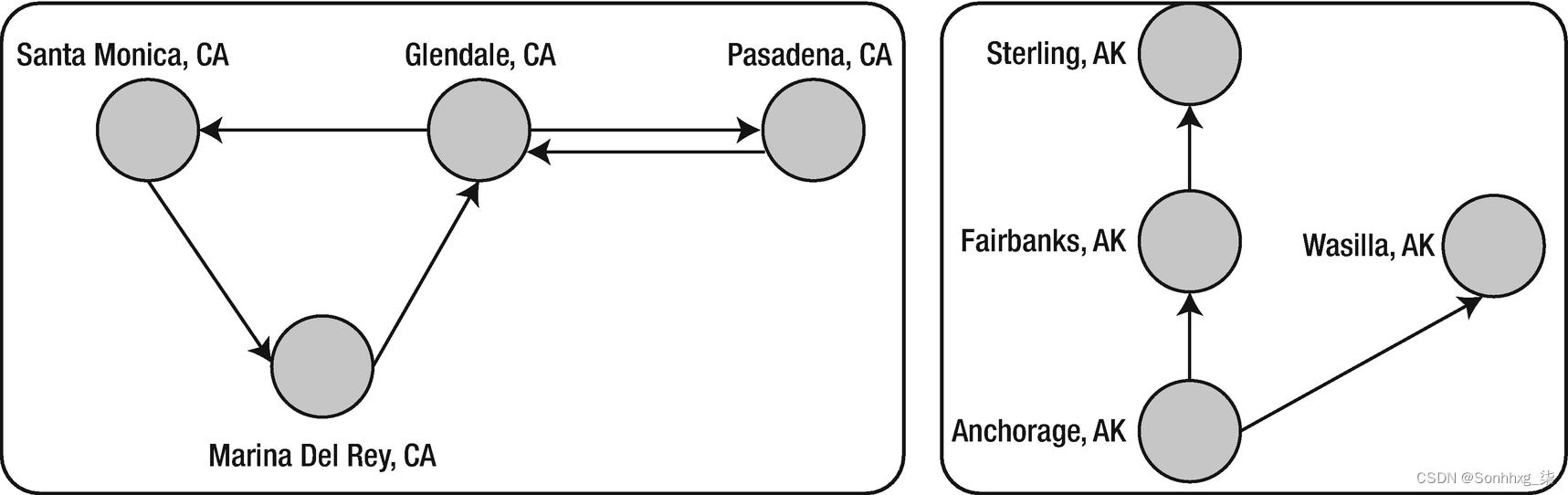
图6-6连接的组件
val vertices = Array((1L, ("Santa Monica","CA")),(2L,("Marina Del Rey","CA")),(3L, ("Glendale","CA")),(4L, ("Pasadena","CA")),(5L, ("Anchorage","AK")),(6L, ("Fairbanks","AK")),(7L, ("Sterling","AK")),(8L, ("Wasilla","AK")))
val vRDD = sc.parallelize(vertices)
val edges = Array(Edge(1L,2L,5),Edge(1L,3L,24),Edge(2L,3L,28),Edge(3L,4L,9),Edge(4L,3L,9),Edge(5L,6L,32),Edge(6L,7L,28),Edge(5L,8L,17))
val eRDD = sc.parallelize(edges)
val graph = Graph(vRDD,eRDD)
graph.vertices.collect.foreach(println)
(6,(Fairbanks,AK))
(3,(Glendale,CA))
(4,(Pasadena,CA))
(1,(Santa Monica,CA))
(7,(Sterling,AK))
(8,(Wasilla,AK))
(5,(Anchorage,AK))
(2,(Marina Del Rey,CA))
graph.edges.collect.foreach(println)
Edge(1,2,5)
Edge(1,3,24)
Edge(2,3,28)
Edge(3,4,9)
Edge(4,3,9)
Edge(5,6,32)
Edge(5,8,17)
Edge(6,7,28)
val connectedComponents = graph.connectedComponents()
connectedComponents.vertices.collect.foreach(println)
(6,5)
(3,1)
(4,1)
(1,1)
(7,5)
(8,5)
(5,5)
(2,1)清单 6-2确定连接的组件
GraphFrames(图形框架)
图形帧是建立在数据帧之上的图形处理库。在撰写本文时,GraphFrames仍在积极开发中,但它成为核心Apache Spark框架的一部分只是时间问题。有几件事使图形框架比GraphX更强大。所有图形帧算法在 Java、蟒蛇和斯卡拉中都可用。可以使用熟悉的数据帧 API 和 Spark SQL 访问图形帧。它还完全支持DataFrame数据源,允许使用多种支持的格式和数据源(如关系数据源,CSV,JSON和镶木地板)读取和写入图形。清单 6-3 显示了如何使用图形帧的示例。
spark-shell --packages graphframes:graphframes:0.7.0-spark2.4-s_2.11
import org.graphframes._
val vDF = spark.createDataFrame(Array((1L, "Santa Monica","CA"),(2L,"Marina Del Rey","CA"),(3L, "Glendale","CA"),(4L, "Pasadena","CA"),(5L, "Anchorage","AK"),(6L, "Fairbanks","AK"),(7L, "Sterling","AK"),(8L, "Wasilla","AK"))).toDF("id","city","state")
vDF.show
+---+--------------+-----+
| id| city|state|
+---+--------------+-----+
| 1| Santa Monica| CA|
| 2|Marina Del Rey| CA|
| 3| Glendale| CA|
| 4| Pasadena| CA|
| 5| Anchorage| AK|
| 6| Fairbanks| AK|
| 7| Sterling| AK|
| 8| Wasilla| AK|
+---+--------------+-----+
val eDF = spark.createDataFrame(Array((1L,2L,5),(1L,3L,24),(2L,3L,28),(3L,4L,9),(4L,3L,9),(5L,6L,32),(6L,7L,28),(5L,8L,17))).toDF("src","dst","distance")
eDF.show
+---+----+--------+
|src|dest|distance|
+---+----+--------+
| 1| 2| 5|
| 1| 3| 24|
| 2| 3| 28|
| 3| 4| 9|
| 4| 3| 9|
| 5| 6| 32|
| 6| 7| 28|
| 5| 8| 17|
+---+----+--------+
val graph = GraphFrame(vDF,eDF)
graph.vertices.show
+---+--------------+-----+
| id| city|state|
+---+--------------+-----+
| 1| Santa Monica| CA|
| 2|Marina Del Rey| CA|
| 3| Glendale| CA|
| 4| Pasadena| CA|
| 5| Anchorage| AK|
| 6| Fairbanks| AK|
| 7| Sterling| AK|
| 8| Wasilla| AK|
+---+--------------+-----+
graph.edges.show
+---+---+--------+
|src|dst|distance|
+---+---+--------+
| 1| 2| 5|
| 1| 3| 24|
| 2| 3| 28|
| 3| 4| 9|
| 4| 3| 9|
| 5| 6| 32|
| 6| 7| 28|
| 5| 8| 17|
+---+---+--------+
graph.triplets.show
+--------------------+----------+--------------------+
| src| edge| dst|
+--------------------+----------+--------------------+
|[1, Santa Monica,...|[1, 3, 24]| [3, Glendale, CA]|
|[1, Santa Monica,...| [1, 2, 5]|[2, Marina Del Re...|
|[2, Marina Del Re...|[2, 3, 28]| [3, Glendale, CA]|
| [3, Glendale, CA]| [3, 4, 9]| [4, Pasadena, CA]|
| [4, Pasadena, CA]| [4, 3, 9]| [3, Glendale, CA]|
| [5, Anchorage, AK]|[5, 8, 17]| [8, Wasilla, AK]|
| [5, Anchorage, AK]|[5, 6, 32]| [6, Fairbanks, AK]|
| [6, Fairbanks, AK]|[6, 7, 28]| [7, Sterling, AK]|
+--------------------+----------+--------------------+
graph.inDegrees.show
+---+--------+
| id|inDegree|
+---+--------+
| 7| 1|
| 6| 1|
| 3| 3|
| 8| 1|
| 2| 1|
| 4| 1|
+---+--------+
graph.outDegrees.show
+---+---------+
| id|outDegree|
+---+---------+
| 6| 1|
| 5| 2|
| 1| 2|
| 3| 1|
| 2| 1|
| 4| 1|
+---+---------+
sc.setCheckpointDir("/tmp")
val connectedComponents = graph.connectedComponents.run
connectedComponents.show
+---+--------------+-----+---------+
| id| city|state|component|
+---+--------------+-----+---------+
| 1| Santa Monica| CA| 1|
| 2|Marina Del Rey| CA| 1|
| 3| Glendale| CA| 1|
| 4| Pasadena| CA| 1|
| 5| Anchorage| AK| 5|
| 6| Fairbanks| AK| 5|
| 7| Sterling| AK| 5|
| 8| Wasilla| AK| 5|
+---+--------------+-----+---------+清单 6-3图形框架示例
总结
本章介绍使用 GraphX 和图形帧进行图形分析。图形分析是一个令人兴奋且快速增长的研究领域,具有广泛而深远的应用。我们只是触及了GraphX和图形框架可以做什么的表面。虽然它可能不适合每个用例,但图形分析非常适合它的设计目的,并且是分析工具集中不可或缺的补充。
以上是关于:图形分析的主要内容,如果未能解决你的问题,请参考以下文章