[Enthought Traning] Scientific Computing in Python

Posted 2022-11-21 ZJun310

[建议打开目录查看]

Enthought Traning

Scientific Computing

---

Data Interpolation

Normal Interpolation

# Data: x y
from scipy.interpolate import interp1d
# Basic
Interpolation = interp1d(x,y)
# With option bounds_error=False, interp1d won't raise an exception on extrapolation
Interpolation = interp1d(x,y,bounds_error = False)
# Fill nan with num when interpolate on extra Interval
Interpolation = interp1d(x,y,bounds_error = False,fill_value=-100)
# Kinds of Interpolation
Interpolation = interp1d(x,y,kind="linear")
# More Opitions : 'nearest','zero','quadratic','cubic',...
#Other Interpolation
from scipy.interpolate import interp2d, interpnd

Radial basis function

Wikipedia

Radial basis functions are typically used to build up function approximations of the form

$$y(\\mathbf x )=\\sum _i=1^Nw_i\\,\\phi (||\\mathbf x -\\mathbf x _i||)$$

Approximation schemes of this kind have been particularly used in time series prediction and control of nonlinear systems exhibiting sufficiently simple chaotic behaviour, 3D reconstruction in computer graphics

Types

• Gaussian

$$\\phi (r)=e^-(\\varepsilon r)^2\\,$$

• Multiquadric:

$$\\phi (r)=\\sqrt 1+(\\varepsilon r)^2$$

• Inverse quadratic

$$\\phi (r)=\\frac 11+(\\varepsilon r)^2$$

• Inverse multiquadric:

$$\\phi (r)=\\frac 1\\sqrt 1+(\\varepsilon r)^2$$

from scipy.interpolate.rbf import Rbf
Interpolation = Rbf(x, y, function = "multiquadric")
from numpy import (linspace, exp, sqrt, mgrid, pi, cos)
from mpl_toolkits.mplot3d import Axes3D
#3D data
x, y = mgrid[-pi/2:pi/2:5j, -pi/2:pi/2:5j]
z = cos(sqrt(x**2 + y**2))

#plot 3D scatter
fig = figure(figsize=(12,6))
ax = fig.gca(projection="3d")
ax.scatter(x,y,z)

#interpolate
zz = Rbf(x, y, z)

#plot 3D surface
xx, yy = mgrid[-pi/2:pi/2:50j, -pi/2:pi/2:50j]
fig = figure(figsize=(12,6))
ax = fig.gca(projection="3d")
ax.plot_surface(xx,yy,zz(xx,yy),rstride=1, cstride=1, cmap=cm.jet)

Statistics in Python

spicy.stats.stats

import scipy.stats.stats as st

Probability Distribution

Continuous Distribution Methods

pdf/cdf/rvs/ppf/stats/fit/sf/isf/entropy/…

Distrete Distribution Methods

pmf/cdf/rvs/ppf/stats/sf/isf/…

Continuous Distribution

from scipy.stats import norm 
from scipy stats import t # t distribution
# generate random variables
x_norm = norm.rvs(size=500)
# fit a specific distribution 
x_mean.x_std = norm.fit(x_norm)
# Draw distribution
x=linspace(-3,3,50)
h = plt.hist(x_norm,normed = Ture ,bins =20)
p = plt.plot(x,norm.pdf(x),'r-')

#calculate probability based on pdf in certain range and then draw the picture
from scipy.stats import norm
from scipy.integrate import trapz
import numpy as np
import matplotlib.pyplot as plt
x1 = np.linspace(-2,2,100)
p = trapz(norm.pdf(x1),x1)
print ':.2%'.format(p)
fb = plt.fill_between(x1,norm.pdf(x1),color = 'gray')
x=np.linspace(-3,3,50)
p = plt.plot(x,norm.pdf(x),'k-')

More about distribution

loc , scale

P = plt.plot(x,norm.pdf(x,loc = 0.5,scale = 2),label = 's=2')
legend()

Discrete Distribution

# Binom / Poisson / uniform distribution
from scipy.stats import binom,poisson,randint

# Binomial Distribution
num_trials = 50
x = arange(num_trials)
p = plot(x, binom(num_trials, 0.5).pmf(x), "o-", label="p=0.5")
p = plot(x, binom(num_trials, 0.2).pmf(x), "o-", label="p=0.2")
l = legend(loc="upper right")
t = title("Binomial distribution with 50 trials")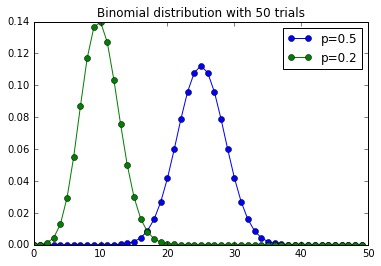

x = arange(0,21)
p = plot(x, poisson(1).pmf(x), 'o-', label=r"$\\lambda$=1")
p = plot(x, poisson(4).pmf(x), 'o-', label=r"$\\lambda$=4")
p = plot(x, poisson(9).pmf(x), 'o-', label=r"$\\lambda$=9")
l = legend()
t = title("Poisson 'number of occurrences' distribution")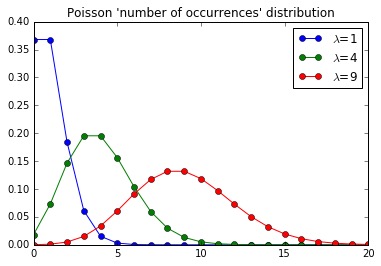

Our Own Discrete Distribution

Can be used in sampling

from scipy.stats import rv_discrete
# Dice Example
xk = [1, 2, 3, 4, 5, 6]
pk = [0.3, 0.35, 0.25, 0.05, 0.025, 0.025]
loaded = rv_discrete(values=(xk, pk))
samples = loaded.rvs(size=100)

Hypothesis Testing

from scipy.stats import norm
from scipy.stats import ttest_ind, ttest_rel, ttest_1samp
#[ttest_ind]Calculates the T-test for the means of TWO INDEPENDENT samples of scores
#[ttest_rel]Calculates the T-test on TWO RELATED samples of scores, before and after
#[ttest_1samp]Calculates the T-test for the mean of ONE group of scores
from scipy.stats import t
n1 = norm(loc=0.5, scale=1.0)
n2 = norm(loc=0, scale=1.0)
n1_samples = n1.rvs(size=100)
n2_samples = n2.rvs(size=100)
# T test
t_val, p_val = ttest_ind(n1_samples, n2_samples)
#t_val = 1.05831471112
#p_val = 0.291201401071

Curve Fitting

Random Generate

np.random.__

Linear polynomial fitting

from numpy import polyfit, poly1d
x = np.linspace(-5, 5, 100)
y = 4 * x + 1.5
noisy_y = y + np.random.randn(y.shape[-1]) * 2.5
coefficients = polyfit(x, noisy_y, 1)
f = poly1d(coefficients) # Generate The Polynomial Function 
#y = poly1d([1,2,3])
#print y
#x^2+2x+3

Least-Squares Fitting

from scipy.linalg import lstsq
from scipy.stats import linregress
from scipy.optimize import leastsq

Transform x

X = np.hstack((x[:,newaxis], np.ones((x.shape[-1],1))))

x = np.linspace(0, 5, 100)
y = 0.5 * x + np.random.randn(x.shape[-1]) * 0.35
X = np.hstack((x[:,newaxis], np.ones((x.shape[-1],1))))
C, resid, rank, s = linalg.lstsq(X, y)
print 'coefficients = '.format(C)
print "sum squared residual = :.3f".format(resid[0])
print "rank of the X matrix = ".format(rank)
print "singular values of X = ".format(s)

slope, intercept, r_value, p_value, stderr = linregress(x, y)

Curve fitting with callables

def fun(x,a,b,c):
    return a*x*x+b*x+c
y= fun(10,*[2,3,4])

General Way For Curve Fitting

from scipy.optimize import curve_fit
def function(x,a,b,c):
    return a*x*x+b*x+c
p_est, err_est = curve_fit(function, x, y)

Minimization

In general, the optimization problems are of the form:

    minimize f(x) subject to
        g_i(x) >= 0,  i = 1,...,m
        h_j(x)  = 0,  j = 1,...,p

    where x is a vector of one or more variables.
    ``g_i(x)`` are the inequality constraints.
    ``h_j(x)`` are the equality constrains.

minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

from scipy.optimize import minimize
def rosenbrock(x,y):
    return (1-x)*(1-x)+100*(y-x*x)*(y-x*x)
x = [3,2]
xi=[x0]
result = minimize(rosen, x0, callback=xi.append)
X_min = result.x
result.fun
#or use 
Fun_minimize = rosenbrock(*result.x)

Symbolic Integration

from sympy import symbols, integrate
import sympy
x, y = symbols('x y')
z = sympy.sqrt(x ** 2 + y **2)
z.subs(x, 3)
z.subs(x, 3).subs(y, 4)

from sympy.abc import theta
y = sympy.sin(theta) ** 2
Y = integrate(y)
#theta/2 - sin(theta)*cos(theta)/2
integrate(y, (theta, 0, sympy.pi))
integrate(y, (theta, 0, sympy.pi)).evalf()

Learn More

import sympy
x ,z= symbols('x z')
y = x*x + sin(x) +3*z
print sympy.diff(y,x)
print sympy.diff(y,z)
m = sympy.diff(y,x)
m.subs(x,2).evalf()

Numerical Integration

Normal integration

from matplotlib.pyplot import plot, annotate, fill_between, figure
import numpy as np
def f(x):
    return x*x
from scipy.integrate import quad
interval = [0, 1]
value, max_err = quad(f, *interval)
x=np.linspace(0,2,20)
plot(x,f(x),'-')
x_interval = np.linspace(0,1,10)
fill_between(x_interval,f(x_interval),color='r',alpha=0.3)
annotate(r"$\\int_0^1x^2dx = $" + ":.3".format(value), (0.5, 2),
         fontsize=16)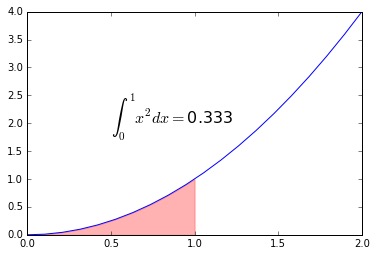

Double integration

Example:

$$I_n(x) = \\int \\limits_0^\\infty \\int \\limits_1^\\infty \\frace^-xtt^ndt dx = \\frac1n$$

from scipy.integrate import dblquad
@vectorize
def I(n):
    x_lower = 0
    x_upper = inf
    return dblquad(h, x_lower, x_upper,lambda t_lower: 1, lambda t_upper: inf, args=(n,))
I([0.5, 1.0, 2.0, 5])

Integration of sampled data

from scipy.integrate import trapz, simps

Trapezoidal Integration

x = linspace(0, pi, 100)
y = sin(x)
result = simps(y, x)

Trapezoidal Integration

x = linspace(0, pi, 100)
y = sin(x)
result = trapz(y, x)