链表相关算法题

Posted 2022-11-17 ~无关风月~

从尾到头打印链表

https://lovezxm.blog.csdn.net/article/details/80781538

反转链表

LeetCode

题目描述：
给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

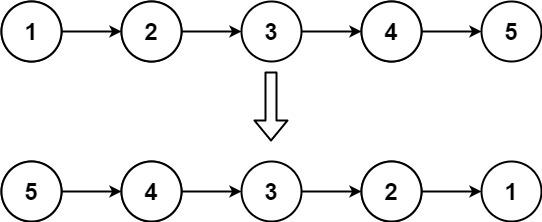
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

题解：
定义pre结点和next结点，head作为当前结点一直推进。

class Solution 

    public ListNode reverseList(ListNode head) 
        ListNode pre = null;
        ListNode next = null;
        while(head != null) 
            next = head.next;
            head.next = pre;
            pre = head;
            head = next;
        
        return pre;
    

复杂度分析
时间复杂度：O(n)，其中 n 指的是链表的大小。
空间复杂度：O(1)。我们只会修改原本链表中节点的指向。

回文链表

LeetCode

题目描述： 给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

输入：head = [1,2,2,1]
输出：true

输入：head = [1,2]
输出：false

进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

题解：

方法一：将值复制到数组中后用双指针法

class Solution 
    public boolean isPalindrome(ListNode head) 
        List<Integer> vals = new ArrayList<Integer>();

        // 将链表的值复制到数组中
        ListNode currentNode = head;
        while (currentNode != null) 
            vals.add(currentNode.val);
            currentNode = currentNode.next;
        

        // 使用双指针判断是否回文
        int front = 0;
        int back = vals.size() - 1;
        while (front < back) 
            if (!vals.get(front).equals(vals.get(back))) 
                return false;
            
            front++;
            back--;
        
        return true;
    

复杂度分析
时间复杂度：O(n)，其中 n 指的是链表的元素个数。
空间复杂度：O(n)，其中 n 指的是链表的元素个数，我们使用了一个数组列表存放链表的元素值。

方法二：递归

使用递归反向迭代节点，同时使用递归函数外的变量向前迭代，就可以判断链表是否为回文。

currentNode 指针是先到尾节点，由于递归的特性再从后往前进行比较。frontPointer 是递归函数外的指针。若 currentNode.val != frontPointer.val 则返回 false。反之，frontPointer 向前移动并返回 true。

class Solution 
    private ListNode frontPointer;

    private boolean recursivelyCheck(ListNode currentNode) 
        if (currentNode != null) 
            if (!recursivelyCheck(currentNode.next)) 
                return false;
            
            if (currentNode.val != frontPointer.val) 
                return false;
            
            frontPointer = frontPointer.next;
        
        return true;
    

    public boolean isPalindrome(ListNode head) 
        frontPointer = head;
        return recursivelyCheck(head);
    

复杂度分析

• 时间复杂度：O(n)，其中 n 指的是链表的大小。
• 空间复杂度：O(n)，其中 n 指的是链表的大小。我们要理解计算机如何运行递归函数，在一个函数中调用一个函数时，计算机需要在进入被调用函数之前跟踪它在当前函数中的位置（以及任何局部变量的值），通过运行时存放在堆栈中来实现（堆栈帧）。在堆栈中存放好了数据后就可以进入被调用的函数。在完成被调用函数之后，他会弹出堆栈顶部元素，以恢复在进行函数调用之前所在的函数。在进行回文检查之前，递归函数将在堆栈中创建n 个堆栈帧，计算机会逐个弹出进行处理。所以在使用递归时空间复杂度要考虑堆栈的使用情况。

方法三：快慢指针（最优）

我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。比较完成后我们应该将链表恢复原样。虽然不需要恢复也能通过测试用例，但是使用该函数的人通常不希望链表结构被更改。

该方法虽然可以将空间复杂度降到 O(1)，但是在并发环境下，该方法也有缺点。在并发环境下，函数运行时需要锁定其他线程或进程对链表的访问，因为在函数执行过程中链表会被修改。

class Solution 
    public boolean isPalindrome(ListNode head) 
        if (head == null) 
            return true;
        

        // 1、找到前半部分链表的尾节点并反转后半部分链表
        ListNode firstHalfEnd = endOfFirstHalf(head);
        // 2、反转后半部分链表
        ListNode secondHalfStart = reverseList(firstHalfEnd.next);

        // 3、判断是否回文
        ListNode p1 = head;
        ListNode p2 = secondHalfStart;
        boolean result = true;
        while (result && p2 != null) 
            if (p1.val != p2.val) 
                result = false;
            
            p1 = p1.next;
            p2 = p2.next;
                

        // 4、还原链表并返回结果
        firstHalfEnd.next = reverseList(secondHalfStart);
        return result;
    

    private ListNode reverseList(ListNode head) 
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) 
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        
        return prev;
    

    private ListNode endOfFirstHalf(ListNode head) 
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) 
            fast = fast.next.next;
            slow = slow.next;
        
        return slow;
    

复杂度分析
时间复杂度：O(n)，其中 n 指的是链表的大小。
空间复杂度：O(1)。我们只会修改原本链表中节点的指向。

环形链表

https://blog.csdn.net/zxm1306192988/article/details/81989082

K 个一组翻转链表

OJ地址

题目描述： 给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

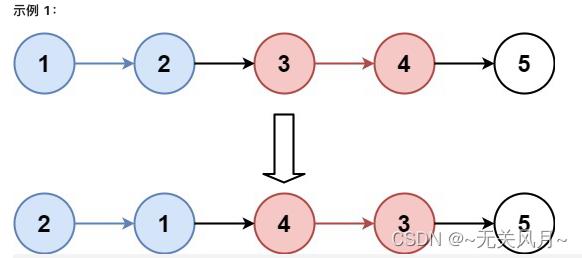
题解：
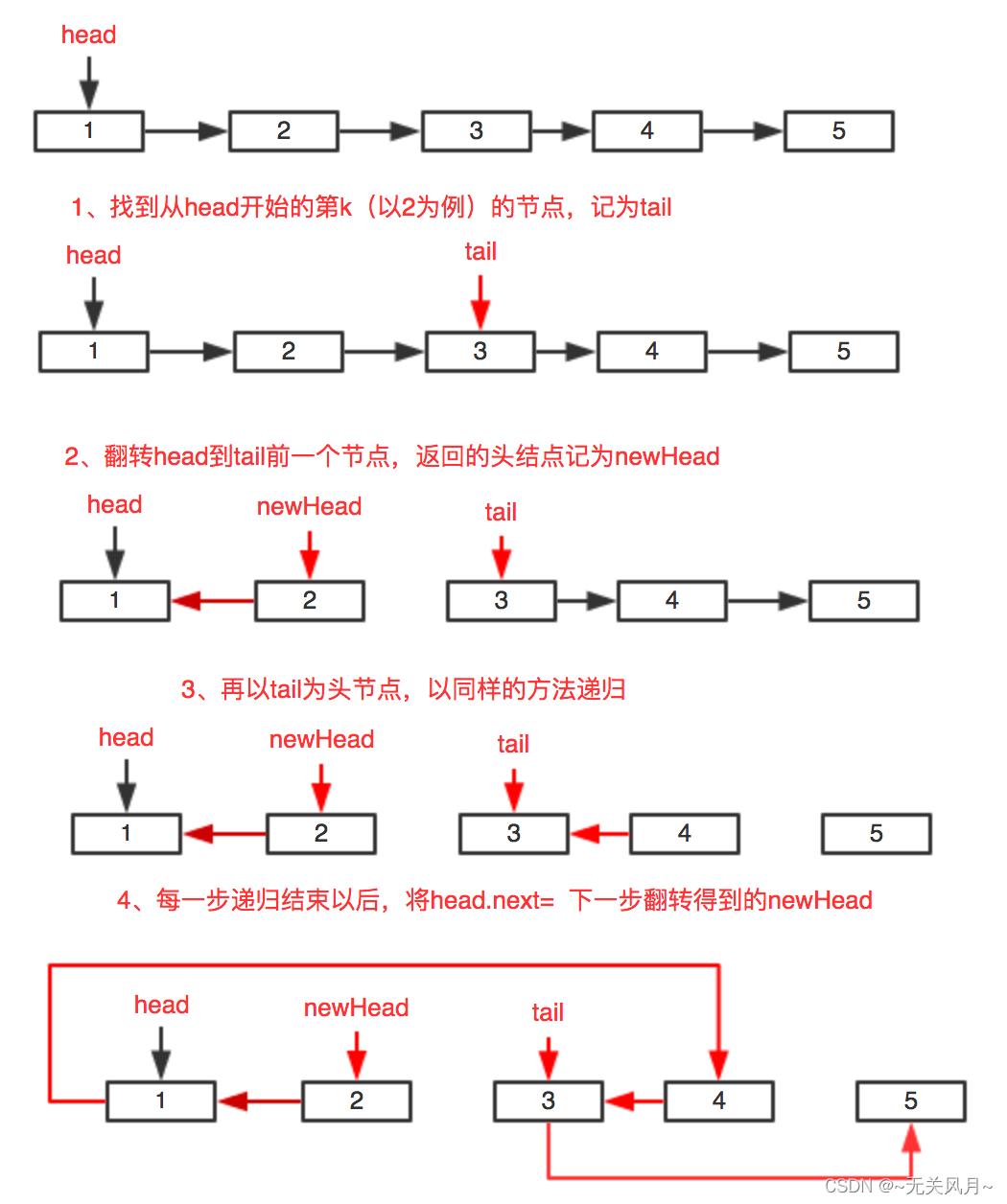
1、规定一轮的翻转范围head到tail 指针，左闭右开，tail 指针从head开始向后移动k次，正常是移动了k次，才可能指到null，如果中途指到null，说明剩余数量小于k，不需要翻转，直接返回头结点。
2、对 [head,tail) 范围内的结点进行翻转，（需要定义pre、next指针移动逐个进行翻转），返回翻转后的新头结点。
3、递归翻转从tail 起的后面的链表，
4、将本段翻转后的尾结点，即老的头结点，指向后段翻转后的头结点。
5、返回本段新的头结点。

import java.io.*;

public class 每K个一组反转链表 

    public static void main(String[] args) throws IOException 
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] strs = br.readLine().split(" ");

        ListNode head = new ListNode(-1);
        ListNode last = head;
        for (String s : strs) 
            last.next = new ListNode(Integer.parseInt(s));
            last = last.next;
        

        int k = Integer.parseInt(br.readLine());
        ListNode node = reverseKGroup(head.next, k);
        while (node != null) 
            System.out.print(node.val + " ");
            node = node.next;
        
    

    public static ListNode reverseKGroup(ListNode head, int k) 
        if (head == null || head.next == null || k <= 1) 
            return head;
        
        ListNode tail = head;
        // 如果剩余的结点小于k,则不翻转，直接返回原头结点
        for (int i = 0; i < k; i++) 
            if (tail == null) 
                return head;
            
            tail = tail.next;
        
        ListNode newHead = reverse(head, tail);
        head.next = reverseKGroup(tail, k);
        return newHead;
    

    /**
     * 翻转链表，左闭，右开
     *
     * @param head
     * @param tail
     * @return
     */
    private static ListNode reverse(ListNode head, ListNode tail) 
        ListNode pre = null;
        ListNode next = null;
        while (head != tail) 
            next = head.next;
            head.next = pre;
            pre = head;
            head = next;
        
        return pre;
    

    static class ListNode 
        int val;
        ListNode next;
        ListNode() 
        
        ListNode(int val) 
            this.val = val;
        
        ListNode(int val, ListNode next) 
            this.val = val;
            this.next = next;
        
    

链表合并

LeetCode

题目描述：将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

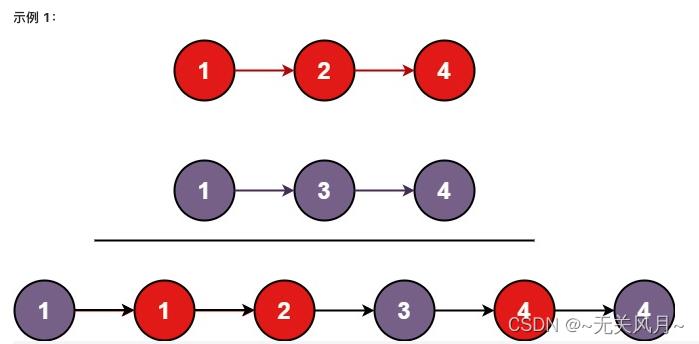
题解：

方法一：递归（优先）

递归地定义两个链表里的 merge 操作（忽略边界情况，比如空链表等）：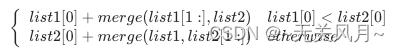
也就是说，两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。

class Solution 
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) 
        if (l1 == null) 
            return l2;
         else if (l2 == null) 
            return l1;
         else if (l1.val < l2.val) 
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
         else 
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        
    

复杂度分析

• 时间复杂度：O(n+m)，其中 n和 m 分别为两个链表的长度。因为每次调用递归都会去掉 l1 或者 l2 的头节点（直到至少有一个链表为空），函数 mergeTwoList 至多只会递归调用每个节点一次。因此，时间复杂度取决于合并后的链表长度，即 O(n+m)。
• 空间复杂度：O(n+m)，其中 n 和 m 分别为两个链表的长度。递归调用 mergeTwoLists 函数时需要消耗栈空间，栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n+m 次，因此空间复杂度为 O(n+m)。

方法二：迭代

当 l1 和 l2 都不是空链表时，判断 l1 和 l2 哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

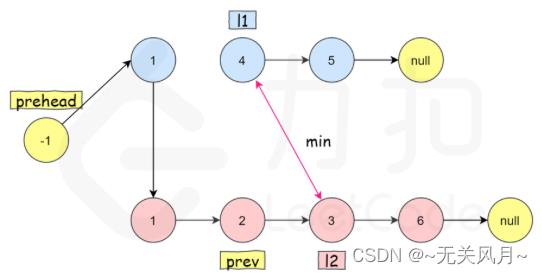
class Solution 
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) 
        ListNode prehead = new ListNode(-1);

        ListNode prev = prehead;
        while (l1 != null && l2 != null) 
            if (l1.val <= l2.val) 
                prev.next = l1;
                l1 = l1.next;
             else 
                prev.next = l2;
                l2 = l2.next;
            
            prev = prev.next;
        

        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev.next = l1 == null ? l2 : l1;

        return prehead.next;
    

复杂度分析

• 时间复杂度：O(n+m)，其中 m 和 n 分别为两个链表的长度。因为每次循环迭代中，l1 和 l2 只有一个元素会被放进合并链表中， 因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为 O(n+m)。
• 空间复杂度：O(1)。我们只需要常数的空间存放若干变量。

找出单向链表中的一个节点，该节点到尾指针的距离为K

OJ地址

题目描述
找出单向链表中的一个节点，该节点到尾指针的距离为K。链表的倒数第0个结点为链表的尾指针。要求时间复杂度为O(n)。
链表结点定义如下：
struct ListNode

int m_nKey;
ListNode* m_pNext;

链表节点的值初始化为1，2，3，4，5，6，7。

输入描述：
该节点到尾指针的距离K

输出描述：
返回该单向链表的倒数第K个节点，输出节点的值

示例1
输入：
2

输出：
6

思路： 用两个指针指向头结点，一个指针先移动k-1步，然后两个指针同步移动，直到第一个指针指向尾结点，此时第二个指针指向的位置即为所求结点。
从输出样例看，最后一个结点算做距离为1，如果最后一个结点算作距离为0，那么只需修改第一个指针先移动k步。

import java.util.*;

public class Main 

    public static void main(String[] args) 
        ListNode head = new ListNode(-1);
        ListNode last = head;
        // 构建链表        
        for (int i = 1; i <= 7; i ++) 
            ListNode temp = new ListNode(i);
            last.next = temp;
            last = last.next;
        
        // 输入k
        Scanner in = new Scanner(System.in);
        int k = in.nextInt();
        // k=0,链表尾就是
        if(k == 0) 
            System.out.println(last.val);
         else 
            ListNode slow = head.next;
            ListNode fast = head.next;
            // fast比slow先走k-1步
            for (int i = 0; i < k - 1; i++) 
                fast = fast.next;
            
            // slow和fast一起走，直到fast到达尾结点，slow就是所求结点
            while (fast.next != null) 
                fast = fast.next;
                slow = slow.next;
            
            System.out.println(slow.val);
        
    

    static class ListNode 
        int val;
        ListNode next;
        ListNode() 
        
        ListNode(int val) 
            this.val = val;
        
        ListNode(int val, ListNode next) 
            this.val = val;
            this.next = next;
        
    

复杂度分析

• 时间复杂度：O(n)，n为链表长度
• 空间复杂度：O(1)。

删除链表的倒数第 N 个结点

LeetCode

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

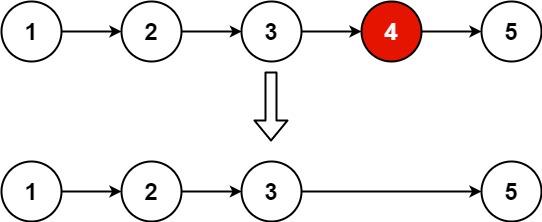
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

题解：
当有删除或插入链表操作的时候要注意了，对于头结点需要特判。
常用的技巧是添加一个哑节点（dummy node），它的 next 指针指向链表的头节点。这样一来，我们就不需要对头节点进行特殊的判断了。

使用快慢指针，起始都指向dummy结点，快指针先移动n个距离，然后快慢指针一起移动，直到快指针指向最后一个结点，此时慢指针指向的就是倒数第n个结点的上一个结点，删除他的下一个结点即可。

class Solution 
    public ListNode removeNthFromEnd(ListNode head, int n) 
        if (head == null) 
            return head;
        
        ListNode dummy = new ListNode(0, head);
        ListNode slow = dummy;
        ListNode fast = dummy;
        while(n > 0) 
            fast = fast.next;
            n --;
        
        while(fast.next != null) 
            slow = slow.next;
            fast = fast.next;
        
        slow.next = slow.next.next;
        return dummy.next;
    

复杂度分析
时间复杂度：O(L)，其中 L 是链表的长度。
空间复杂度：O(1)。