如果你还不懂区块链那就out了（三)--区块链3.0的优秀解决方案：Hyperledger fabric

Posted 2023-04-05 stalin_

前面我们提到，在区块链3.0中，已经发展出了智能合约+私有链的形式，而目前这种形式应用最广泛的就是今天要说的：Hyperledger fabric。

一、Hyperledger fabric 介绍

Hyperledger Fabric，是一个基于模块化架构的分布式账本解决方案平台，它是由 IBM 带头发起的一个联盟链项目，于 15 年底移交给 Linux 基金会，成为开源项目。Hyperledger 基金会的成员有很多大牌，诸如 IBM，Intel，思科等。基金会里孵化了很多区块链项目，Fabric 是其中最出名的一个，一般我们说超级账本（Hyperledger）基本上指的都是 Fabric。
Hyperledger fabric 不是货币技术，是区块链技术。所以fabric没有挖矿的概念，绿色环保。

二、Hyperledger fabric的优势

1、分布式的账本存储
2、每一个节点都保存了完整的数据，从而实现了数据不可被篡改
3、区块链中的数据不能被删除，只能添加和修改，变化后的数据状态为World State（世界状态）

三、使用Hyperledger fabric解决现实问题

假如A公司与B公司要进行资产交换，数据都存储在自己的服务器
由于A公司和B公司互不信任，所以两公司之间要进行对账，实际上往往账目是对不上的

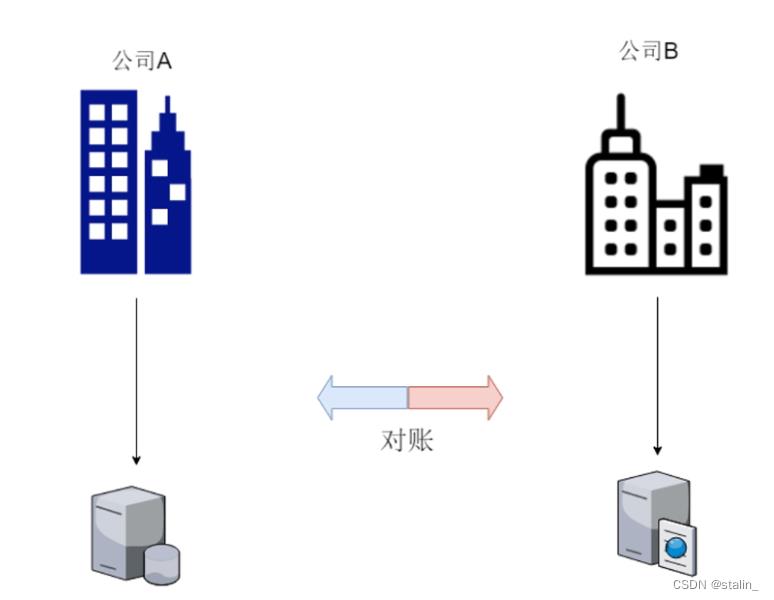一般传统解决方案：

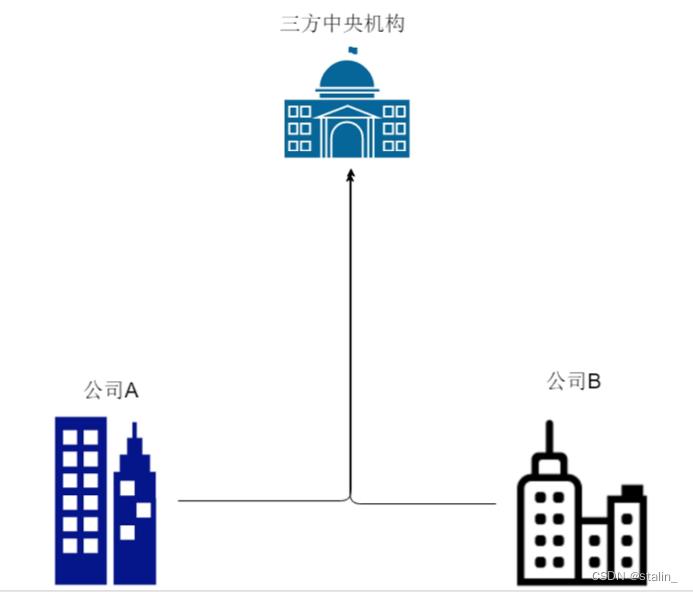
通过引入第三方中央机构解决，实际上这种方式也是存在问题的：
1、成本高
2、三方机构的安全问题
通过Hyperledger fabric解决：

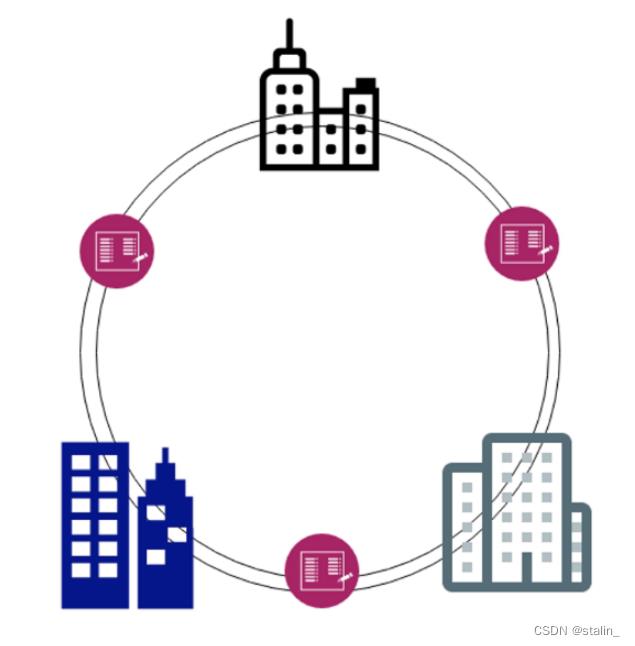
1、将各个机构形成环状，每个结构都有自己的账本，数据都一致。
2、fabric保证数据的同步。
3、如果有A机构做了数据篡改，其他机构就会发现A机构的数据发生了错误。
4、实际上，fabric解决就是信任问题。

案例分析

项目：江苏省农牧厅区块链渔政管理系统

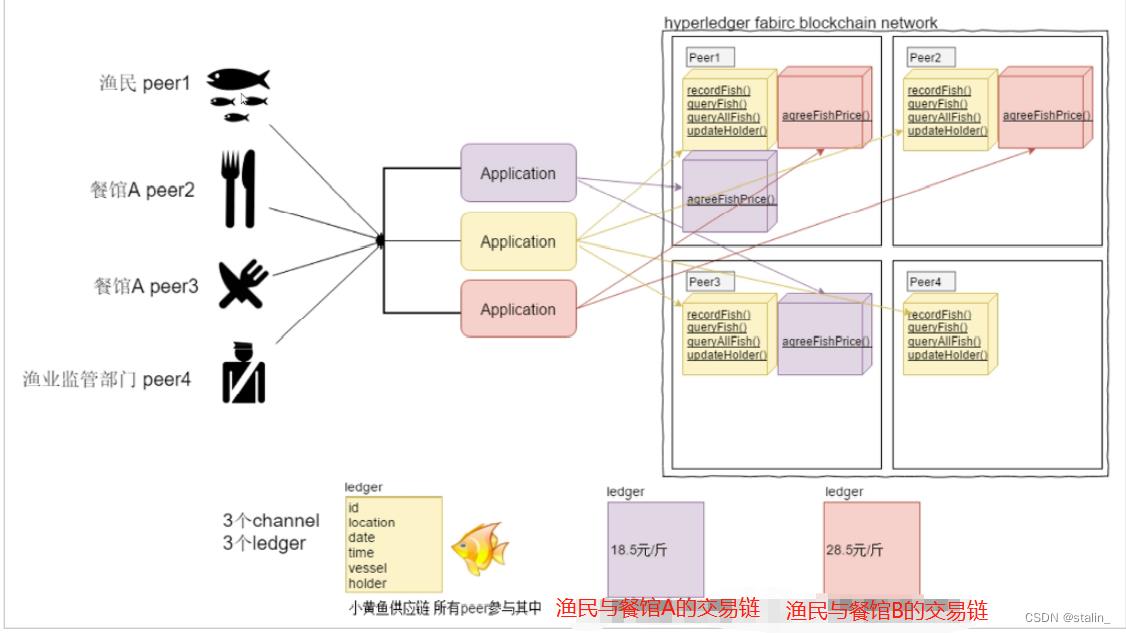
渔业供应链参与人

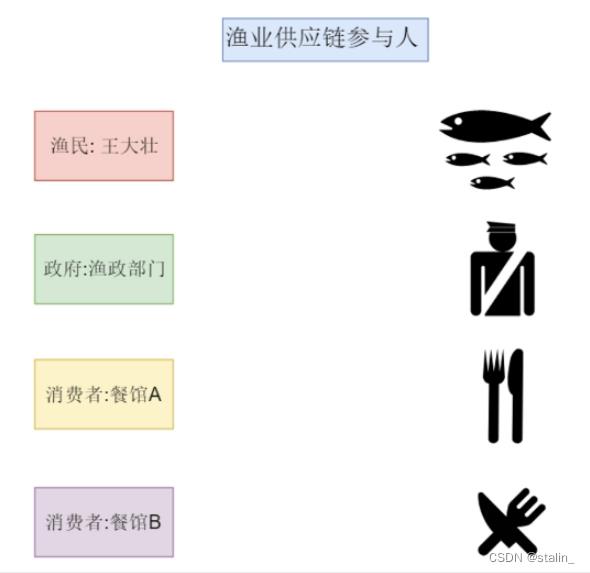
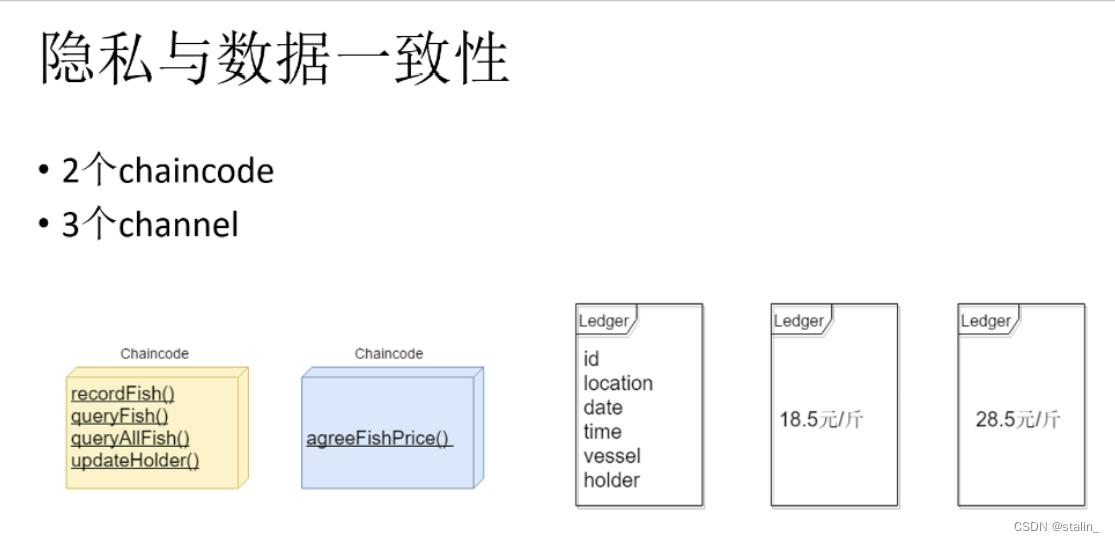
channel

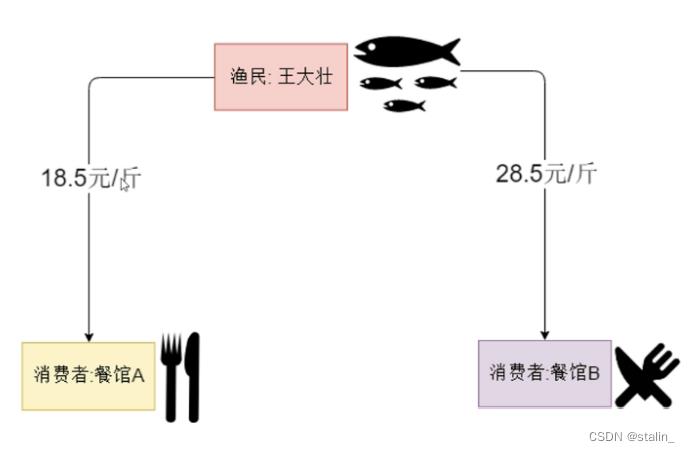
如果，王大壮与餐馆A和餐馆B的交易放在同一个channel的话，那么价格的隐私数据得不到保障。
在Hyperledger fabric中，channel可以理解为是独立的实例。参与者称之为peer。
实际上可以理解为两个微信群，

chaincode（智能合约）

Chaincode就是智能合约。是读取、修改数据的唯一途径。
Chaincode属于某个channel，channel中的peer都需要安装该Chaincode，否则会导致数据不一致。
Chaincode的生命周期为：
1）安装 install
2）实例化 init
3）调用 invoke

工作流程

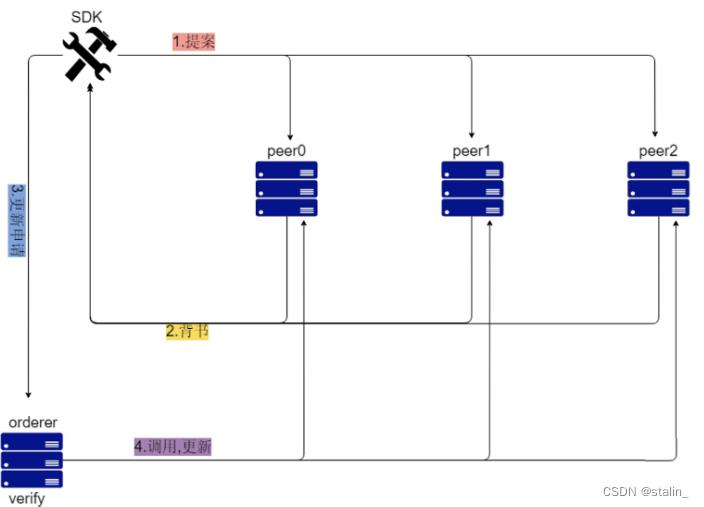
SDK是为客户端提供操作的API，和实现语言无关。

peer

1）peer0、peer1、peer2在同一个channel中
2）多个peer必须有相同的MSP（Membership Service Provider）才能进行通信。

提案

1）客户端通过SDK发起提案，如：我需要修改某一条数据了。
2）各个peer接收到提案后，进行模拟执行，会产生读写集，内部采用version的机制来记录修改前后的状态。

背书

1）各个peer将模拟执行后的结果以及签名，发送给SDK

更新申请

1）SDK收集到一定数量的背书后，将发送正式的更新申请给orderer

orderer

1）对请求的内容以及签名做校验
2）如果校验完成，没有问题的话，就会发送真正的调用更新给各个peer，各个peer才真正的执行更新。
3）如果不合法的请求，也会保存到block chain，方便后续的审查。
4）排序解决双花问题，解决方式为把并行的问题转化成串行执行。

项目中的实际应用

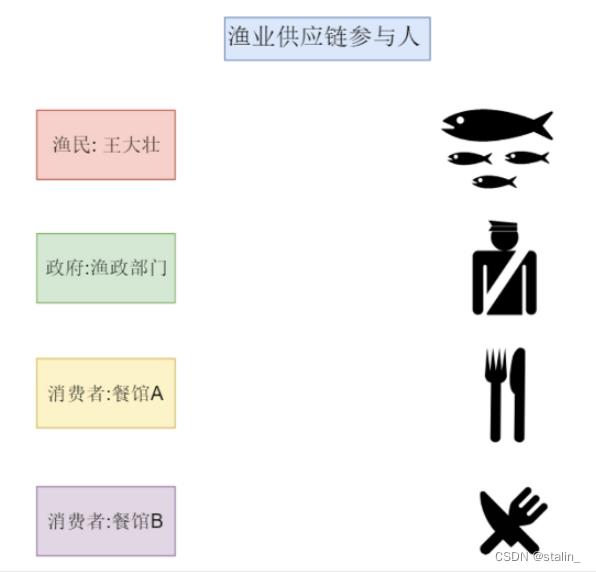
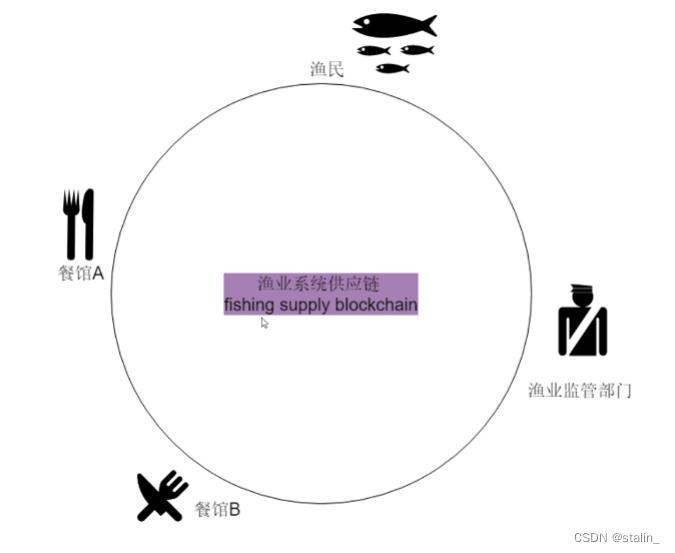
痛点的本质就是信任问题：
1）餐馆不信任王大壮
2）监管部门不信任餐馆
3）监管部门不信任王大壮
4）王大壮的隐私问题

如果看了此文你还不懂傅里叶变换，那就过来掐死我吧完整版 - 博客 - 伯乐在线

• 手机UI设计基础-尺寸
• Cocos2d-x基础教程二-会动的时钟
• Android摄像头基础
• Golang之IO操作初接触

原文出处： 韩昊   

1 2 3 4 5 6 7 8 9 10

作 者：韩 昊 知 乎：Heinrich 微 博：@花生油工人 知乎专栏：与时间无关的故事   谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。   转载的同学请保留上面这句话，谢谢。如果还能保留文章来源就更感激不尽了。   ——更新于2014.6.6，想直接看更新的同学可以直接跳到第四章————

我保证这篇文章和你以前看过的所有文章都不同，这是 2012 年还在果壳的时候写的，但是当时没有来得及写完就出国了……于是拖了两年，嗯，我是拖延症患者……

这篇文章的核心思想就是：

要让读者在不看任何数学公式的情况下理解傅里叶分析。

傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是，傅里叶分析的公式看起来太复杂了，所以很多大一新生上来就懵圈并从此对它深恶痛绝。老实说，这么有意思的东西居然成了大学里的杀手课程，不得不归咎于编教材的人实在是太严肃了。（您把教材写得好玩一点会死吗？会死吗？）所以我一直想写一个有意思的文章来解释傅里叶分析，有可能的话高中生都能看懂的那种。所以，不管读到这里的您从事何种工作，我保证您都能看懂，并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友，也希望不要看到会的地方就急忙往后翻，仔细读一定会有新的发现。

————以上是定场诗————

下面进入正题：

抱歉，还是要啰嗦一句：其实学习本来就不是易事，我写这篇文章的初衷也是希望大家学习起来更加轻松，充满乐趣。但是千万！千万不要把这篇文章收藏起来，或是存下地址，心里想着：以后有时间再看。这样的例子太多了，也许几年后你都没有再打开这个页面。无论如何，耐下心，读下去。这篇文章要比读课本要轻松、开心得多……

一、什么是频域

从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。但如果我告诉你，用另一种方法来观察世界的话，你会发现世界是永恒不变的，你会不会觉得我疯了？我没有疯，这个静止的世界就叫做频域。

先举一个公式上并非很恰当，但意义上再贴切不过的例子：

在你的理解中，一段音乐是什么呢？

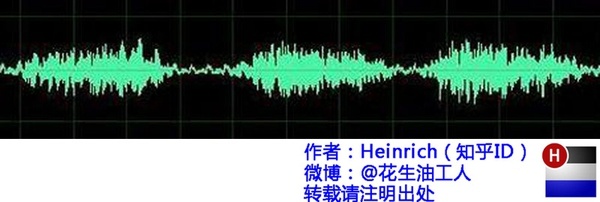
这是我们对音乐最普遍的理解，一个随着时间变化的震动。但我相信对于乐器小能手们来说，音乐更直观的理解是这样的：

好的！下课，同学们再见。

是的，其实这一段写到这里已经可以结束了。上图是音乐在时域的样子，而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生，只是从来没意识到而已。

现在我们可以回过头来重新看看一开始那句痴人说梦般的话：世界是永恒的。

将以上两图简化：

时域：

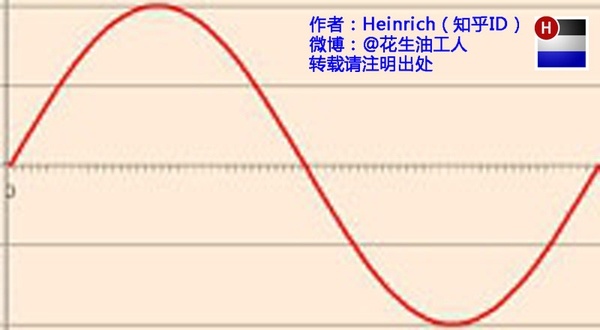
频域：

在时域，我们观察到钢琴的琴弦一会上一会下的摆动，就如同一支股票的走势；而在频域，只有那一个永恒的音符。

所以

你眼中看似落叶纷飞变化无常的世界，实际只是躺在上帝怀中一份早已谱好的乐章。

抱歉，这不是一句鸡汤文，而是黑板上确凿的公式：傅里叶同学告诉我们，任何周期函数，都可以看作是不同振幅，不同相位正弦波的叠加。在第一个例子里我们可以理解为，利用对不同琴键不同力度，不同时间点的敲击，可以组合出任何一首乐曲。

而贯穿时域与频域的方法之一，就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换(Fourier Transformation)，我们从简单的开始谈起。

 

二、傅里叶级数(Fourier Series)的频谱

还是举个栗子并且有图有真相才好理解。

如果我说我能用前面说的正弦曲线波叠加出一个带 90 度角的矩形波来，你会相信吗？你不会，就像当年的我一样。但是看看下图：

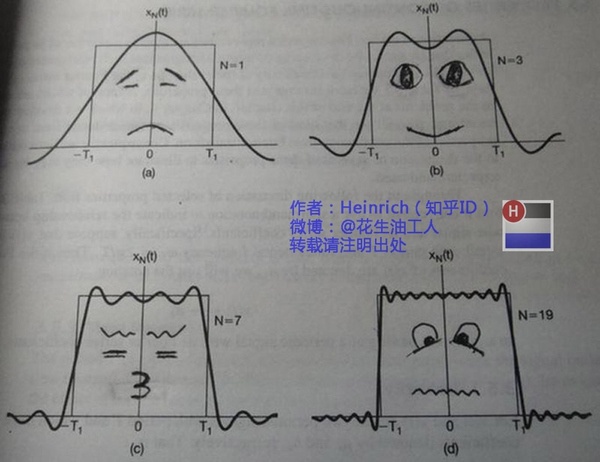
第一幅图是一个郁闷的正弦波 cos（x）

第二幅图是 2 个卖萌的正弦波的叠加 cos (x) +a.cos (3x)

第三幅图是 4 个发春的正弦波的叠加

第四幅图是 10 个便秘的正弦波的叠加

随着正弦波数量逐渐的增长，他们最终会叠加成一个标准的矩形，大家从中体会到了什么道理？

（只要努力，弯的都能掰直！）

随着叠加的递增，所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡，而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢？不幸的告诉大家，答案是无穷多个。（上帝：我能让你们猜着我？）

不仅仅是矩形，你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点，但是一旦接受了这样的设定，游戏就开始有意思起来了。

还是上图的正弦波累加成矩形波，我们换一个角度来看看：

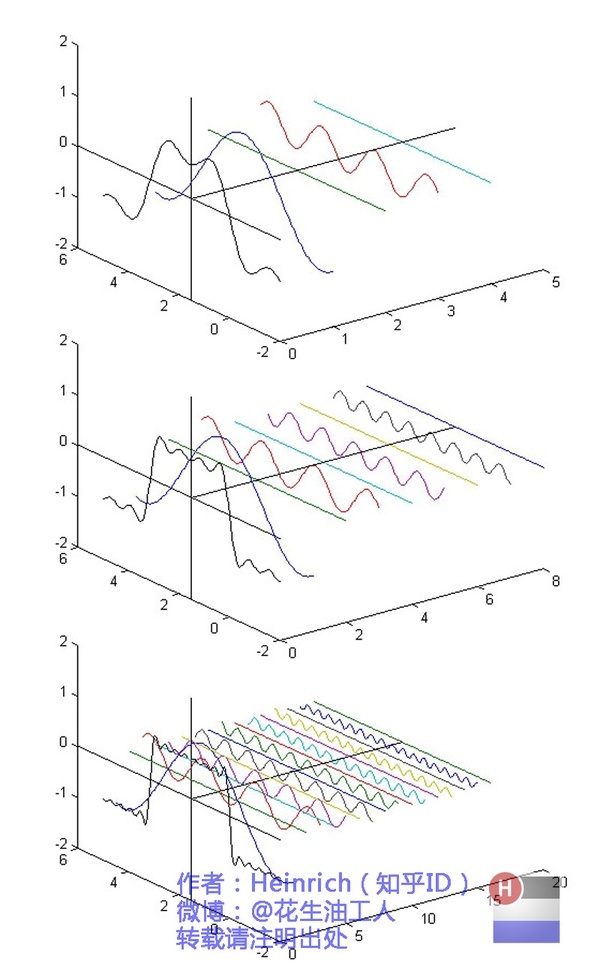
在这几幅图中，最前面黑色的线就是所有正弦波叠加而成的总和，也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来，而每一个波的振幅都是不同的。一定有细心的读者发现了，每两个正弦波之间都还有一条直线，那并不是分割线，而是振幅为 0 的正弦波！也就是说，为了组成特殊的曲线，有些正弦波成分是不需要的。

这里，不同频率的正弦波我们成为频率分量。

好了，关键的地方来了！！

如果我们把第一个频率最低的频率分量看作“1”，我们就有了构建频域的最基本单元。

对于我们最常见的有理数轴，数字“1”就是有理数轴的基本单元。

（好吧，数学称法为——基。在那个年代，这个字还没有其他奇怪的解释，后面还有正交基这样的词汇我会说吗?）

时域的基本单元就是“1 秒”，如果我们将一个角频率为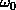的正弦波 cos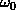（t）看作基础，那么频域的基本单元就是。

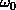有了“1”，还要有“0”才能构成世界，那么频域的“0”是什么呢？cos（0t）就是一个周期无限长的正弦波，也就是一条直线！所以在频域，0 频率也被称为直流分量，在傅里叶级数的叠加中，它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。

接下来，让我们回到初中，回忆一下已经死去的八戒，啊不，已经死去的老师是怎么定义正弦波的吧。

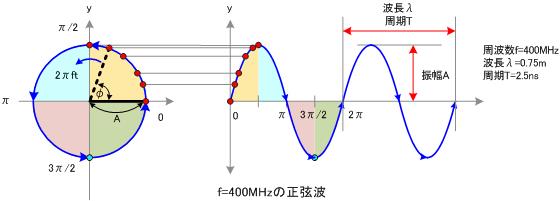
正弦波就是一个圆周运动在