logistic regression与最大熵模型·最大熵模型

Posted 2022-11-13 tina_ttl

李航·统计学习方法笔记·第6章 logistic regression与最大熵模型（2）·最大熵模型

标签（空格分隔）： 机器学习教程·李航统计学习方法

---

• 李航统计学习方法笔记第6章 logistic regression与最大熵模型2最大熵模型
• 最大熵原理
  • 1 最大熵原理的基本内容
  • 2 最大熵原理的几何意义
• 最大熵模型
  • 1 到底应该如何表示分类模型
  • 2 最大熵模型的约束条件
    • 21 最大熵模型的一个总述
    • 22 特征函数feature function
    • 23 如何计算经验分布
  • 3 最大熵模型的具体内容
• 最大熵模型的学习
  • 1 最大熵模型的求解
  • 2 例子
• 最大熵模型学习的等价形式
• 逻辑斯蒂回归模型和最大熵模型
• 参考文献

注意，这里有一个前提，这里讨论的分类模型都是概率模型！
最大熵模型是另外一种机器学习模型，与逻辑斯蒂回归模型没有什么关系，只不过被安排在了一个章节讲解

---

最大熵原理只是一个学习的准则，利用这个准则可以从一堆概率模型中选择一个最优的

1 最大熵原理

最大熵模型是根据最大熵原理推导得到的，所以，为了推导最大熵模型，必须首先了解最大熵原理！

1.1 最大熵原理的基本内容

• 最大熵原理认为：在所有可能的概率模型中，熵最大的模型为最好的概率模型（下图中的阶段2）
  

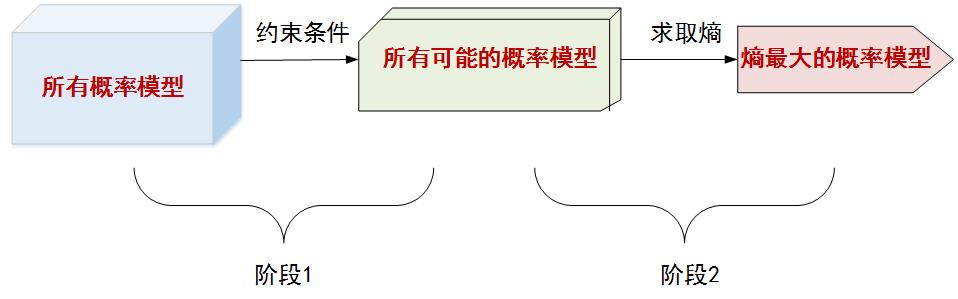
• 这里的“所有可能的概率模型”是一个概率模型的集合，是在所有的概率模型中，根据一定的约束条件选取出来的（上图中的阶段1）

  不知道能否这样理解？？？
  比如，对应逻辑斯蒂回归模型中，它使用的用来表示分类器的模型其实就是利用逻辑斯蒂分布构造的一个概率分布，这个概率分布的形式是一定的，只不过参数待求，那么，可以将这些形式一定但参数未知的概率分布看着是“所有可能的概率模型”的集合，在这个集合中，找到熵最大的那个模型，也就实现了参数的求解

• 综上，最大熵原理可以表述为：在满足约束条件的概率模型集合中选取熵最大的模型

  那么，如何计算概率模型的熵呢？$\\rightarrow$先讨论离散情况

  对于某一个随机变量X，它的概率分布为P(X)（即PMF或者说是分布律），它的熵定义为
  

  $$H(P) = -\\sum_i=1^nP(x_i)\\logP(x_i)$$
  它表述的是随机变量X取得所有可能值 $x_i$( $i=1,\\cdots,n$)带来的自信息的数学期望，即表征了该信号带来的信息量！

  ---

  上面的熵的取值范围是什么呢？
  

  $$0 \\leqslant H(P) \\leqslant \\logn$$
  具体推导过程见《最优化理论·拉格朗日Lagrange对偶性的一个实例》

• 所以，最大熵原理的具体内容或者说是实际使用方法为：

  • 根据已有的信息（约束条件），选择适当的概率模型
  • 对于那些不确定的部分，认为它们是等可能的，也就实现了最大熵的目的
  • 那这个方法如何使用呢？下面给出一个实际的例子：
    
    
    • 首先，根据已知条件，可以得到下面的约束：
      
      除此信息外，不再有其他可利用信息，那么，根据最大熵原理（不确定的信息认为其为等可能），则有
      
    • 如果接下来又添加了一个可用信息
      
      则此时，再根据最大熵原理，可以得到
      

1.2 最大熵原理的几何意义

• 下图是所有可能的概率模型空间（用一个2单纯形表示），所有可能的概率空间位于三角形内部
  
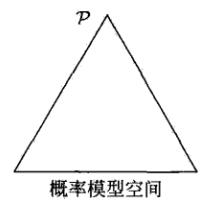
• 现在加入了两个约束条件，此时的概率空间变小了，变成了图中的5条之间的某个交集围成的区间（由于这里并没有给出两个约束的具体内容，所以这个区间还不能确定，可能是下图中的四个子区间的任何一个）
  

2 最大熵模型

2.1 到底应该如何表示分类模型？

• 对于分类问题，它的分类模型可以表示条件概率分布：$P(Y|X)$

• 例如，对于一个三分类的分类问题，这个分类模型其实就是一个离散型的条件概率分布，每个类别$Y$的概率取值都有一个模型$P(Y=i|X)$，它不是一个具体的取值，而是一个与输入的样本$X=x$（$x$为一个特征向量）相关的一个函数：可以认为，该表就是要求解的分类器！！！

可能取值	类别1	类别2	类别3
分布律	$P(Y=1|X)$ $P(Y=2|X)$ $P(Y=3|X)$ 通俗理解 函数$p_1(x)$ 函数函数$p_2(x)$ 函数$p_3(x)$ 再以逻辑斯蒂回归问题的模型$P(Y|X)$为例 可能取值 Y=1 Y=0 概率 $P(Y=1|X)=\\frac\\exp(wx)1+\\exp(wx)$ $P(Y=0|X)=\\frac11+\\exp(wx)$ 通俗理解 函数$p_1(x)$是$x$的函数 函数函数$p_2(x)$是$x$的函数 2.2 最大熵模型的约束条件 2.2.1 最大熵模型的一个总述 利用最大熵原理去求解上面所述的条件概率(应用于分类问题中），得到的分类模型就是最大熵模型 那么，应该如何做呢？ 给定一个训练数据集 $$T = \\(x_1,y_1),(x_2,y_2),\\cdots,(x_N,y_N)\\ $$ 其中： $N$为训练集中样本个数； $x_i \\in X$（输入空间）为输入，它其实是一个向量，代表的是输入样本的特征； yi∈Y以上是关于logistic regression与最大熵模型·最大熵模型的主要内容，如果未能解决你的问题，请参考以下文章 logistic regression与最大熵模型·逻辑斯蒂回归模型 logistic regression与最大熵模型·逻辑斯蒂回归模型 Logistic Regression几问 Logistic Regression几问 逻辑斯谛回归与最大熵模型-《统计学习方法》学习笔记 第六章 逻辑斯蒂回归与最大熵模型