算法设计与分析实训
Posted Time木0101
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法设计与分析实训相关的知识,希望对你有一定的参考价值。
文末也可直接获取实训文档
算法设计与分析实训
目录
1. 题目
0-1背包问题
2. 目的
课程设计的目的是训练学生灵活应用所学数据结构知识,独立完成问题分析、总体设计、详细设计和编程实现等软件开发全过程的综合实践能力。巩固、深化学生的理论知识,提高编程水平,并在此过程中培养他们严谨的科学态度和良好的工作作风。课程设计要求独立完成一个较为完整的应用需求分析,在完成设计和编程大型作业的同时,达到如下效果:
(1)深化对算法与数据结构课程中基本概念、理论和方法的理解;
(2)训练综合运用所学知识处理实际问题的能力;
(3)使程序设计与调试水平有一个明显的提高;
(4)培养科学的软件工作方法。
3. 内容
(1) 分析问题,进行问题建模,根据模型选择合适的数据结构。
(2) 物品编号、重量、价值信息来源于文件。
(3) 根据选定的数据结构选择算法设计策略,设计两种以上算法。
(4) 根据算法设计策略设计算法。
(5) 分析算法的时间复杂度和空间复杂度,并比较算法优劣。
(6) 讨论算法改进、优化方法。
4. 需求分析
(1)问题描述:准确的要求编程解决的问题。
假设有n个物品和1个背包,每个物品i对应价值为vi,重量wi,背包的容量为W。每个物品只有1件,要么装入,要么不装入,不可拆分。在背包不超重的情况下,如何选取物品装入背包,使所装入的物品的总价值最大?最大价值是多少?装入了哪些物品?
(2)功能要求:给出程序要实现的功能。
输入物品的个数n和购物车的容量W数据以及每个物品的重量w和价值v
(3)数据要求:输入的形式和值的范围;输出的形式
请输入物品的个数n:
请输入购物车的容量W:
请依次输入每个物品的重量w和价值v,用空格分开:
(4)测试数据:设计测试数据,或具体给出测试数据。要求测试数据能全面地测试所设计程序的功能。
输入数据:5
10
2 6 5 3 4 5 2 4 3 6
5. 两种算法
5.1动态规划法
5.1.1分析问题,进行问题建模,根据模型选择合适的数据结构。
有n个物品,每个物品的重量为w[],价值为v[i],购物车的容量为W。选若千个物品
放入购物车,在不超过容量的前提下使获得的价值最大。
(1)确定合适的数据结构
采用一-维数组w[i]、v[j]来记录第i个物品的重量和价值:二维数组用c[i][i]表示前i件物品放入-一个容量为j的购物车可以获得的最大价值。
(2)初始化
初始化c[][]数组0行0列为0: c[0][i]=0, c[i][0]=0, 其中i=0,1, 2,.,. n, j=0,1,2,…,W。
(3)循环阶段
a.按照递归式计算第1个物品的处理情况,得到c[1][i], j=1, 2,.,. W。
按照递归式计算第2个物品的处理情况,得到c[2][j], j=1, 2,.,. W。
b.以此类推,按照递归式计算第n个物品的处理情况,得到c[n][], j=1, 2,.,. W。
(4)构造最优解
c[n][W]就是不超过购物车容量能放入物品的最大价值。如果还想知道具体放入了哪些物品,就需要根据c[[数组逆向构造最优解。我们可以用一-维数组x[i]来存储解向量。
a.首先i=n,j=W,如果c[i][]>c[i-1][],则说明第n个物品放入了购物车,令x[n]=1,
j-=w[n]; 如果c[i][j]≤c[i-1]i],则说明第n个物品没有放入购物车,令x[n]=0。
b.i–,继续查找答案。
c.直到i=1处理完毕。
这时已经得到了解向量(x[1], x[2], … ,x[n]),可以直接输出该解向量,也可以仅把x[i]=1的货物序号i输出。
5.1.2 详细设计
(1)各个抽象数据类型的存储结构类型定义。
(2)算法思想及伪码:描述解决相应问题算法的设计思想并设计出相应伪码。
a.装入购物车最大价值求解
c[i][i]表示前i件物品放入一个容量为j的购物车可以获得的最大价值。
对每一个物品进行计算,购物车容量j从1递增到W,当物品的重量大于购物车的容量,
则不放此物品,c[i][j]=c[i- 1][j],否则比较放与不放此物品是否能使得购物车内的物品价值最大,即c[i[j]=max (c[i-1][j], c[i-1][j-w[i] + v[i])。
for(i=1;i<= n;i++) //计算c[i] [j]
for(j=1;j<=W;j++)
if(j<w[i]) //当物品的重量大于购物车的容量,则不放此物品
c[i][j] = c[i-1][j];
else //否则比较此物品放与不放是否能使得购物车内的价值最大
c[i][j] = max(c[i-1] [j],c[i-1] [j-w[i]] + v[i]) ;
cout<<"装入购物车的最大价值为:"<<c[n] [W]<<end1;
b.最优解构造
根据c[][]数组的计算结果逆向递推最优解,可以用-一个一一维数组x[]记录解向量,x[i]=1表示第i个物品放入了购物车,x[i]=0 表示第i个物品没放入购物车。
首先i=n,j=W:如果c[j[i]>c[i-1][],说明第i个物品放入了购物车,x[i]=1, j-=w[i]; 否则x[i]=0。
i=n-1:如果c[i][]>c[i-1][],说明第i个物品放入了购物车, x[i]=1,j- =w[i];否则x[i]=0。
......
i=1;如果c[i][i]>c[i- 1][j],说明第i个物品放入了购物车,x[i]=1,j-=w[];否则x[i]=0。
我们可以直接输出x[i]解向量,也可以只输出放入购物车的物品序号。
//逆向构造最优解
j=W;
for(i=n;i>0;i--)
if(c[i][j]>c[i-1][j])
x[i]=1;
j-=w[i];
else
x[i]=0;
cout<< “装入购物车的物品为:”;
for(i=1;i<=n;i++)
if(x[i]==1)
cout<<i<<””;
(3)画出函数和过程的调用关系图。
5.1.3编码与调试
(1)给出所有源程序清单,要求程序有充分的注释语句,至少要注释每个函数参数的含义和函数返回值的含义。
#include <iostream>
#include <cstring>
using namespace std;
#define maxn 100005
#define M 105
int c[M] [maxn] ; //c[i][j]表示前i个物品放入容量为j购物车获得的最大价值
int w[M] ,v[M] ; //w[i]表示第i个物品的重量,v[i]表示第i个物品的价值
int x[M]; //x[i]表示第i个物品是否放入购物车
int main()
int i,j,n,W; //n 表示n个物品,W表示购物车 的容量
cout << "请输入物品的个数n: ";
cin >> n;
cout << "请输入购物车的容量W: ";
cin >> W;
cout << "请依次输入每个物品的重量w和价值v,用空格分开: ";
for(i=1;i<=n;i++)
cin>>w[i]>>v[i];
for(i=0;i<=n;i++) //初始化第 0列为0
c[i] [0]=0;
for(j=0;j<=W;j++) //初始化第0 行为0
c[0] [j]=0;
for(i=1;i<= n;i++) //计算c[i] [j]
for(j=1;j<=W;j++)
if(j<w[i]) //当物品的重量大 于购物车的容量,则不放此物品
c[i][j] = c[i-1] [j] ;
else //否则比较此物品放与不放是否能使得购物车内的价值最大
c[i] [j] = max(c[i-1][j],c[i-1] [j-w[i]] + v[i]) ;
cout<<"装入购物车的最大价值为: "<<c[n] [W]<<endl;//逆向构造最优解
j=W;
for(i=n; i>0;i--)
if(c[i][j]>c[i-1] [j])
x[i]=1;
j-=w[i] ;
else
x[i]=0;
cout<<"装入购物车的物品为: ";
for(i=1;i<=n; i++)
if(x[i]==1)
cout<<i << " ";
return 0;
(2)调试程序过程中遇到的问题以及如何解决,
(3)算法的时间和空间复杂度的分析。
时间复杂度:算法中有主要的是两层嵌套的for循环,其时间复杂度为O(nW)。
空间复杂度:由于二维数组c[n][W], 所以空间复杂度为O(n W)。
5.1.4 测试与结果分析
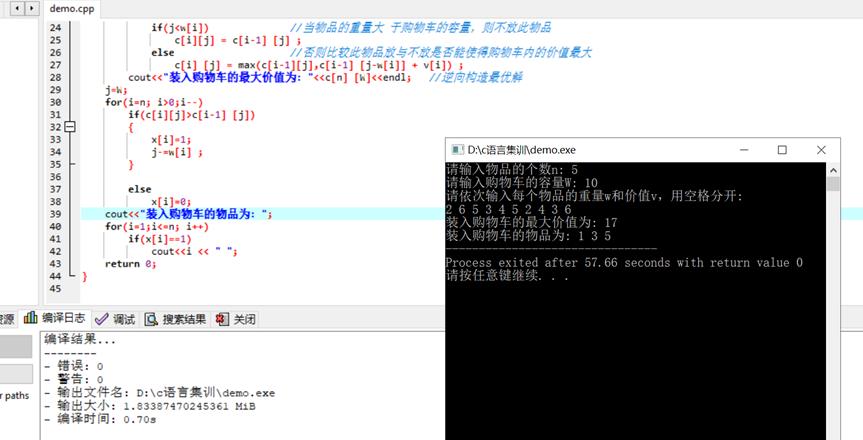
5.1.5算法优化
首先有-一个主循环i=1, 2,… N,每次算出来二维数组c[i][0w]的所有值。那么,如果只用一个数组dp[0W], 能不能保证第i次循环结束后dp[i]中表示的就是我们定义的状态c[i][j]呢? c[i][]由c[i-1]i]和c[i-1] [j-w[]两个子问题递推而来,能否保证在递推c[i][i]时 (也即在第i次主循环中递推dp[j]时) 能够得到c[i-1][]和c[i-1][j-w[i]的值呢? 事实上,这要求在每次主循环中以j=W,W-1, .,. 1, 0的顺序倒推dp[i],这样才能保证递推dp[j]时dp[i- c[i]保存的是状态c[i -1][j-w[i]的值。
伪代码如下:
for i=1. .n
for j=W. .0
dp[j]=maxdp[j] ,dp[j-w[i]]+v[i];
其中,dp[i]=max dp[i],dp[i- w[i]就相当于转移方程c[i][j]=maxc[i -1][j], c[i-1][j-w[],因为这里的dp[j- w[i]就相当于原来的c[i-1][j- w[i]]。
#include <iostream>
#include<cstring>
using namespace std;
#define maxn 10005
#define M 105
int dp [maxn] ; //dp[j]表示当前已放入容量为j的购物车获得的最大价值
int w[M],v[M]; //w[i]表示第 i个物品的重量, v[i]表示第i个物品 的价值
int x[M]; //x[i]表示第i个物品是否放入购物车
int i,i,n,W; //n表示n个物品,W表示购物车的容量
void opt1 (int n, int W)
for(i=1;i<=n;i++)
for(j=W;j>n;j--)
if(j>=w[i]) // 当购物车的容量大于等于物品的重量,比较此物品放与不放是否
能使得购物车内的价值最大
dp[j] = max(dp[j],dp[j-w[i]]+v[i]) ;
int main()
cout << "请输入物品的个数n:";
cin >> n;
cout << "请输入购物车的容量w:";
cin >> W;
cout << "请依次输入每个物品的重量w和价值v,用空格分开:";
for(i=1; i<=n; i++)
cin>>W[i]>>v[i] ;
for(j=1;j<=W;j++)//初始化第0行为0
dp[j]=0;
opt1 (n,W) ;
//opt2(n,W) ;
//opt3(n,W) ;
cout<<"装入购物车的最大价值为: "<<dp[W]<<endl;
/ /测试dp[]数组结果
for(j=1;j<=W;j++)
cout<<dp[j]<<" ";
cout<<endl;
return 0;
其实我们可以缩小范围,因为只有当购物车的容量大于等于物品的重量时才要更新(dp[j]= max (dp[j],dp[j- w[i]+v[i])),如果当购物车的容量小于物品的重量时,则保持原来的值(相
当于原来的c[i-1][j])即可。因此第2个for语句可以是for(j=W; j>=w[i]; j–), 而不必搜
索到j=0。
void opt2(int n,int W)
for(i=1;i<= n;i++)
for (j=W;j>=w[i];j--)
//当购物车的容量大于等于物品的重量,比较此物品放与不放是否能使得购物车内的价值最大
dp[j] = max(dp[j] ,dp[j-w[i]]+v[i]) ;
我们还可以再缩小范围,确定搜索的下界bound,搜索下界取w[i]与剩余容量的最大值,
sum[n] -sum[i- 1]表示i~n的物品重量之和。W- (sum[n] -sum[i- 1])表示剩余容量。
因为只有购物车容量超过下界时才要更新(dp[i] = max (dp[i], dp[j- w[i]]+v[i])),如果
购物车容量小于下界,则保持原来的值(相当于原来的c[i-1][j)即可。因此第2个for语
句可以是for(j=W; j>=bound; j--), 而不必搜索到j=0。
void opt3(int n, int W)
int sum[n];//sum[i]表示从 1~i的物品重量之和
sum[0]=0;
for (i=l;i<=n; i++)
sum[i]=sum[i-1] +W[i] ;
for (i=1; i<=n;i++)
int bound=max (w[i],W- (sum [n]-sum[i-1]));//搜索下界,w[i]与剩余容量取
最大值,sum[n]-sum[i-1]表示从i...n的物品重量之和
for (j=w;j>=bound;j--)
//购物车容量大于等于下界,比较此物品放与不放是否能使得购物车内的价值最大
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
5.2回溯法
5.2.1分析问题,进行问题建模,根据模型选择合适的数据结构。
(1)定义问题的解空间
购物车问题属于典型的0-1背包问题,问题的解是从n个物品中选择一些物品使其在不,
超过容量的情况下价值最大。每个物品有且只有两种状态,要么装入购物车,要不不装入。
那么第i个物品装入购物车,能够达到目标要求,还是不装入购物车能够达到目标要求呢?
很显然,目前还不确定。因此,可以用变量x;表示第i种物品是否被装入购物车的行为,如果用“0”表示不被装入背包,用“1”表示装入背包,则x;的取值为0或1。i=1, 2, … n第i个物品装入购物车,x=1;不装入购物车,x=0。该问题解的形式是一个n元组,且每个分量的取值为0或1。
由此可得,问题的解空间为x,x2,. xi, …, xn,其中,显约束xi;=0或1,i=1,
2,…, n。
(2)确定解空间的组织结构
问题的解空间描述了2” 种可能解,也可以说是n个元素组成的集合所有子集个数。例如3个物品的购物车问题,解空间是: 0, 0,0, 0, 0, 1,0, 1,0,0, 1, 1, 1,0,0,1,0,1,1,1,0,1,1,1。该问题有23个可能解。
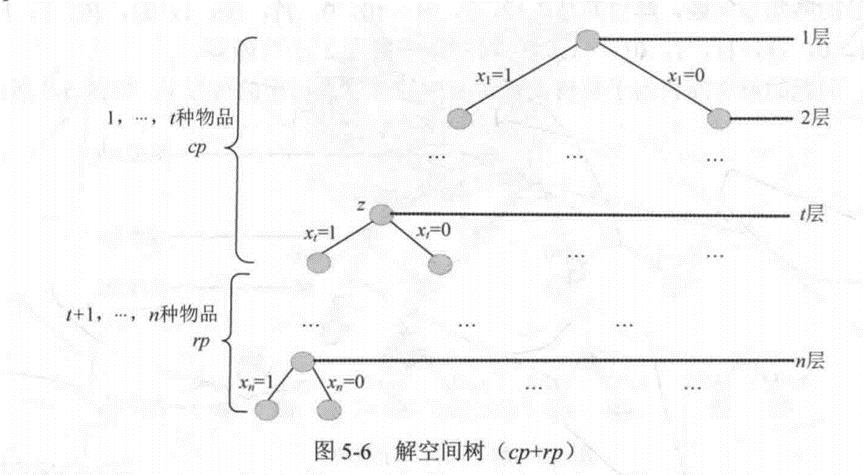
可见,问题的解空间树为子集树,解空间树的深度为问题的规模n,如图5-5所示。

(3)搜索解空间
约束条件
购物车问题的解空间包含2^n种可能解,存在某种或某些物品无法装入购物车的情况,因此需要设置约束条件,判断装入购物车的物品总重量是否超出购物车容量,如果超出,为不可行解;否则为可行解。搜索过程不再搜索那些导致不可行解的结点及其孩子结点。
约束条件为:
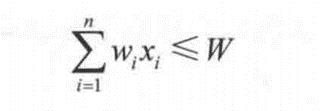
限界条件
购物车问题的可行解可能不止一个,问题的目标是找一个装入购物车的物品总价值最大
的可行解,即最优解。因此,需要设置限界条件来加速找出该最优解的速度。根据解空间的组织结构,对于任何一个中间结点z (中间状态),从根结点到z结点的分支所代表的状态(是否装入购物车)已经确定,从z到其子孙结点的分支的状态是不确定的。也就是说,如果z在解空间树中所处的层次是t,说明第1种物品到第t-1种物品的状态已经确定了。我们只需要沿着z的分支扩展很容易确定第t种物品的状态。那么前t种物品的状态就确定了。但第t+1种物品到第n种物品的状态还不确定。这样,前t种物品的状态确定后,当前已装入购物车的物品的总价值,用cp表示。已装入物品的价值高不一定 就是最优的,因为还有剩余物品未确定。我们还不确定第t+1种物品到第n种物品的实际状态,因此只能用估计值。假设第t+1种物品到第n种物品都装入购物车,第t+1种物品到第n种物品的总价值用rp来表示,因此cp+rp是所有从根出发经过中间结点z的可行解的价值上界,如图5-6所示。
如果价值上界小于或等于当前搜索到的最优值(最优值用bestp表示,初始值为0),则
说明从中间结点z继续向子孙结点搜索不可能得到一个比当前更优的可行解,没有继续搜索
的必要,反之,则继续向z的子孙结点搜索。
限界条件为:
cp+rp>bestp
搜索过程
从根结点开始,以深度优先的方式进行搜索。根节点首先成为活结点,也是当前的扩展
结点。由于子集树中约定左分支上的值为“1”,因此沿着扩展结点的左分支扩展,则代表装入物品。此时,需要判断是否能够装入该物品,即判断约束条件成立与否,如果成立,即生成左孩子结点,左孩子结点成为活结点,并且成为当前的扩展结点,继续向纵深结点扩展;
如果不成立,则剪掉扩展结点的左分支,沿着其右分支扩展,右分支代表物品不装入购物车,
肯定有可能导致可行解。但是沿着右分支扩展有没有可能得到最优解呢?这一点需要由限界
条件来判断。如果限界条件满足,说明有可能导致最优解,即生成右孩子结点,右孩子结点
成为活结点,并成为当前的扩展结点,继续向纵深结点扩展;如果不满足限界条件,则剪掉
扩展结点的右分支,向最近的祖宗活结点回溯。搜索过程直到所有活结点变成死结点结束。
5.2.2详细设计
(1)各个抽象数据类型的存储结构类型定义。
(2)算法思想及伪码:描述解决相应问题算法的设计思想并设计出相应伪码。
a.计算上界
计算上界是指计算已装入物品价值cp与剩余物品的总价值rp之和。我们已经知道已装入购物车的物品价值cp,剩余物品我们不确定要装入哪些,我们按照假设都装入的情况估算,即按最大值计算(剩余物品的总价值),因此得到的值是可装入物品价值的上界。
double Bound(int i)//计算 上界(即已装入物品价值+剩余物品的总价值)
int rp=0; //剩余物品为第i~n种物品
while(i<=n) //依次计算剩余物品的价值
rp+=v[i] ;
i ++;
return cp+rp;//返回上界
(2)按约束条件和限界条件搜索求解
t表示当前扩展结点在第t层,cw表示当前已放入物品的重量,cp 表示当前已放入物品的价值。
如果t>n,表示已经到达叶子结点,记录最优值最优解,返回。否则,判断是否满足约束条件,满足则搜索左子树。因为左子树表示放入该物品,所以x[t]=1,表示放入第t个该物品。cw+=w[t],表示当前已放入物品的重量增加w[t]。cp+=v[t], 表示当前已放入物品的价值增加v[t]。Backtrack(t+1)表示递推,深度优先搜索第t+1层。回归时即向上回溯时,要把增加的值减去,cw-=w[t], cp- =v[t]。
判断是否满足限界条件,满足则搜索右子树。因为右子树表示不放入该物品,所以令x[t]=0。当前已放入物品的重量、价值均不改变。Backtrack(t+1)表示递推, 深度优先搜索第t+1层。
void Backtrack(int t) //t表示当前扩展结点在第t层
if (t>n) //已经到达叶子结点
for(j=1;j<=n;j++)
bestx[j]=x[j];
bestp=cp; //保存当前最优解
return ;
if (cw+w[t]<=W) //如果满足约束条件则搜索左子树
x[t]=1;
CW+=w[t] ;
cp+=v[t] ;
Backtrack(t+1) ;
CW-=W[t] ;
cp-=v[t] ;