关于旅行家TSP问题的几种算法 python

Posted 2023-04-04

参考技术A

问题描述不展开了，感兴趣可以自己搜一下。csdn上这篇文章介绍的很详细，可以看一下 ， http://blog.csdn.net/q345852047/article/details/6626684 感谢作者辛勤码字，我就偷懒啦～

1.贪心

c=[[0,3,1,5,8],
[3,0,6,7,9],
[1,6,0,4,2],
[5,7,4,0,3],
[8,9,2,3,0]]
n=len(c)

d=[[0 for j in range(2**(n-1))] for i in range(n)]
for i in range(1,n): # 1234
d[i][0]=c[i][0]

"""0 000
1 001 1
2 002 2
3 011 1,2
4 100 3
5 101 1,3
6 110 2,3
7 111 1,2,3
"""

def judge(i,j):#3=1+2 5=101 1+3 6=3+2
involve=(i&j)==0#结果为0说明不包含
return involve #若j不包含i 返回true

def find_vertex(j):
vertexs=[]#j包含哪几个顶点
for v in range(n-1):
if (2 v)&j!=0:#0123 2 i表示顶点i+1
vertexs.append(v+1) #说明j包含顶点v+1
return vertexs

for j in range(2 (n-1)):# j从0-15
for i in range(1,n):# 1234
temp=[]
vertexes=find_vertex(j)
if i not in vertexes:
for k in vertexes:
temp.append(c[i][k]+d[k][j-2 (k-1)])
if temp:
d[i][j]=min(temp)
print(d[i][j])

temp=[]
for k in find_vertex(2 (n-1)-1):
j=2 (n-1)-1
new_j=2 (n-1)-1-2 (k-1)
temp.append(c[0][k]+d[k][new_j])
d[0][2**(n-1)-1]=min(temp)

print("Shortest path length:",d[0][2**(n-1)-1])
for row in d:
for col in row:
print(str(col)+" ",end="")
print()

遗传算法GA--TSP旅行商问题（Python）

文章目录

• • 一.基础介绍
  • 二.分布实现
  • 三.完整代码
  • 四.结果截图

一.基础介绍

遗传算法的来源、定义、特点见之前的文章【遗传算法GA】–计算函数最值（Python）。

---

下面我们先来看本次需要实现的内容：我们随机生成一些城市的坐标，然后找一条最短路径通过所有城市。

最重要的还是对染色体DNA的编码以及适应度函数的确定。对于本题来说可以先将所以城市进行编号，然后对这些编号进行排序，排好的顺序就是旅行的路线。对于适应度函数来说就是将路程加起来，总路程最小，适应度越高。

参数:

参数名称	含义
citys	城市个数
pc	交叉概率
pm	变异概率
popsize	种群规模
iternum	迭代次数
pop	种群
city_position	城市坐标

二.分布实现

$\bullet$ 参数：

citys = 20 #染色体DNA长度
pc = 0.1 #交叉概率
pm = 0.02 #变异概率
popsize = 500 #种群规模
iternum = 100 #迭代次数

GA类:

$\bullet$ 将种群中排好的序列横纵坐标分别提取出来transltaeDNA函数：参数DNA为种群pop，参数city_position为所有城市坐标

def translateDNA(self,DNA,city_position):
    #生成等长的空列表
    lineX = np.empty_like(DNA,dtype=np.float64)
    lineY = np.empty_like(DNA,dtype=np.float64)
    #将下标和值同时提取出来
    for i,d in enumerate(DNA):
        city_coord = city_position[d]
        lineX[i,:] = city_coord[:,0]
        lineY[i,:] = city_coord[:,1]
    return lineX,lineY

$\bullet$ 求适应度函数getFiness：参数lineX、lineY分别为城市坐标，返回fitness为每个个体的适应度，totalDis为每个个体的总路程。

def getFitness(self,lineX,lineY):
    totalDis = np.empty((lineX.shape[0],),dtype=np.float64)
    for i,(xval,yval) in enumerate(zip(lineX,lineY)):
        totalDis[i]=np.sum(np.sqrt(np.square(np.diff(xval)) + np.square(np.diff(yval))))
    fitness = np.exp(self.citys*2/totalDis)
    return fitness,totalDis

$\bullet$ 选择函数selection：参数fitness为适应度，选择适应度更高的个体。

def selection(self,fitness):
    idx = np.random.choice(np.arange(self.popsize),size=self.popsize,replace=True,p=fitness/fitness.sum())
    return self.pop[idx]

$\bullet$ 交叉函数selection：参数parent为父本中一个个体，pop为种群。

交叉规则：在交叉概率内随机选择种群中一个体，随机选择一些位置，将这些位置的数提取出来放到数组前面，然后将母本中除这些数之外的数按顺序放入数组后面，组成新个体。

def crossover(self,parent,pop):
    if np.random.rand() < self.pc:
        i = np.random.randint(0, self.popsize, size=1)  #随机选取一个个体进行交换                      
        cross_points = np.random.randint(0, 2, self.citys).astype(np.bool)   #随机选择个体中的一些位置
        keep_city = parent[~cross_points]     #将parent中False的位置返给keep_city                                  
        swap_city = pop[i, np.isin(pop[i].ravel(), keep_city, invert=True)]  #将keep_city中没有出现的数赋给swap_city
        parent[:] = np.concatenate((keep_city, swap_city)) #拼接形成新个体
    return parent

$\bullet$ 变异函数mutation：在变异范围内随机选取一个位置与下标位置的数进行互换。

def mutation(self,child):
    for point in range(self.citys):
        if np.random.rand()<self.pm:
            swap_point = np.random.randint(0,self.citys)
            swapa,swapb = child[point],child[swap_point]
            child[point],child[swap_point] = swapb,swapa
    return child

$\bullet$ 进化函数evolve：调用交叉函数和变异函数。

def evolve(self,fitness):
    pop = self.selection(fitness)
    pop_copy = pop.copy()
    for parent in pop: 
        child = self.crossover(parent,pop_copy)
        child = self.mutation(child)
        parent[:] = child
    self.pop = pop

TSP类：

$\bullet$ 构造函数：随机生成城市坐标

def __init__(self,citys):
    #生成每个城市的横纵坐标
    self.city_position = np.random.rand(citys,2)
    plt.ion()

$\bullet$ 绘图函数plotting：参数lx、ly为城市横纵坐标，total_d最优路线。

def plotting(self,lx,ly,total_d):
    plt.cla()
    plt.scatter(self.city_position[:, 0].T, self.city_position[:, 1].T, s=100, c='k')  #画散点图
    plt.plot(lx.T, ly.T, 'r-') #连线
    plt.text(-0.05, -0.05, "Total distance=%.2f" % total_d, fontdict={'size': 20, 'color': 'red'})
    plt.xlim((-0.1, 1.1))
    plt.ylim((-0.1, 1.1))
    plt.pause(0.01)

$\bullet$ 主函数：

if __name__=='__main__':
    ga = GA(citys=citys,pc=pc,pm=pm,popsize=popsize)
    env = TSP(citys=citys)
    
    for gen in range(iternum):
        lx,ly = ga.translateDNA(ga.pop,env.city_position)
        fitness,total_distance = ga.getFitness(lx,ly)
        ga.evolve(fitness)
        best_idx = np.argmax(fitness) #最优解的下标
        print("Gen:", gen," | best fit: %.2f"%fitness[best_idx],)
        
        env.plotting(lx[best_idx],ly[best_idx],total_distance[best_idx])
    
    plt.ioff()
    plt.show()

三.完整代码

import numpy as np
import matplotlib.pyplot as plt


#参数
citys = 20 #染色体DNA长度
pc = 0.1 #交叉概率
pm = 0.02 #变异概率
popsize = 500 #种群规模
iternum = 100 #迭代次数

class GA(object):
    def __init__(self,citys,pc,pm,popsize,):
        self.citys = citys
        self.pc = pc
        self.pm = pm
        self.popsize = popsize
        
        #vstck纵向拼接数组，permutaion将数字0-（city-1）进行随机排序
        #生成种群，dna序列为0到city的随机序列
        self.pop = np.vstack([np.random.permutation(citys) for _ in range(popsize)])
    
    #将种群中排好的序列横纵坐标分别提取出来
    def translateDNA(self,DNA,city_position):
        #生成等长的空列表
        lineX = np.empty_like(DNA,dtype=np.float64)
        lineY = np.empty_like(DNA,dtype=np.float64)
        #将下标和值同时提取出来
        for i,d in enumerate(DNA):
            city_coord = city_position[d]
            lineX[i,:] = city_coord[:,0]
            lineY[i,:] = city_coord[:,1]
        return lineX,lineY

    
    def getFitness(self,lineX,lineY):
        totalDis = np.empty((lineX.shape[0],),dtype=np.float64)
        for i,(xval,yval) in enumerate(zip(lineX,lineY)):
            totalDis[i]=np.sum(np.sqrt(np.square(np.diff(xval)) + np.square(np.diff(yval))))
        fitness = np.exp(self.citys*2/totalDis)
        return fitness,totalDis
        
    def selection(self,fitness):
        idx = np.random.choice(np.arange(self.popsize),size=self.popsize,replace=True,p=fitness/fitness.sum())
        return self.pop[idx]
        
    def crossover(self,parent,pop):
        if np.random.rand() < self.pc:
            i = np.random.randint(0, self.popsize, size=1)  #随机选取一个个体进行交换                      
            cross_points = np.random.randint(0, 2, self.citys).astype(np.bool)   #随机选择个体中的一些位置
            keep_city = parent[~cross_points]     #将parent中False的位置返给keep_city                                  
            swap_city = pop[i, np.isin(pop[i].ravel(), keep_city, invert=True)]  #将keep_city中没有出现的数赋给swap_city
            parent[:] = np.concatenate((keep_city, swap_city)) #拼接形成新个体
        return parent
        
    def mutation(self,child):
        for point in range(self.citys):
            if np.random.rand()<self.pm:
                swap_point = np.random.randint(0,self.citys)
                swapa,swapb = child[point],child[swap_point]
                child[point],child[swap_point] = swapb,swapa
        return child
            
    def evolve(self,fitness):
        pop = self.selection(fitness)
        pop_copy = pop.copy()
        for parent in pop: 
            child = self.crossover(parent,pop_copy)
            child = self.mutation(child)
            parent[:] = child
        self.pop = pop
            
        
    
class TSP(object):
    def __init__(self,citys):
        #生成每个城市的横纵坐标
        self.city_position = np.random.rand(citys,2)
        plt.ion()
        
    def plotting(self,lx,ly,total_d):
        plt.cla()
        plt.scatter(self.city_position[:, 0].T, self.city_position[:, 1].T, s=100, c='k')  #画散点图
        plt.plot(lx.T, ly.T, 'r-') #连线
        plt.text(-0.05, -0.05, "Total distance=%.2f" % total_d, fontdict={'size': 20, 'color': 'red'})
        plt.xlim((-0.1, 1.1))
        plt.ylim((-0.1, 1.1))
        plt.pause(0.01)
        
if __name__=='__main__':
    ga = GA(citys=citys,pc=pc,pm=pm,popsize=popsize)
    env = TSP(citys=citys)
    
    for gen in range(iternum):
        lx,ly = ga.translateDNA(ga.pop,env.city_position)
        fitness,total_distance = ga.getFitness(lx,ly)
        ga.evolve(fitness)
        best_idx = np.argmax(fitness) #最优解的下标
        print("Gen:", gen," | best fit: %.2f"%fitness[best_idx],)
        
        env.plotting(lx[best_idx],ly[best_idx],total_distance[best_idx])
    
    plt.ioff()
    plt.show()
    
    

    

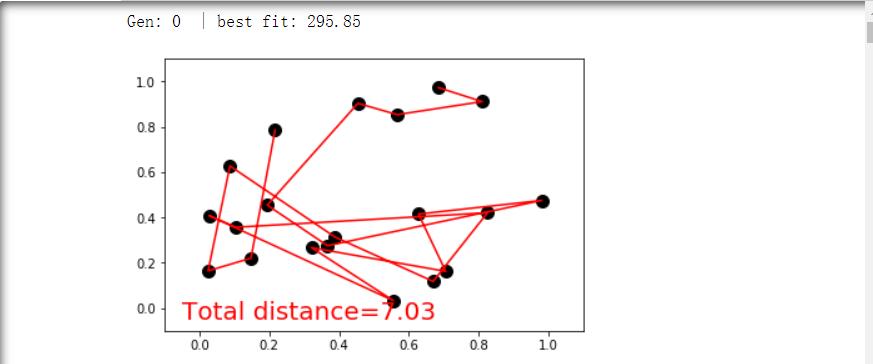
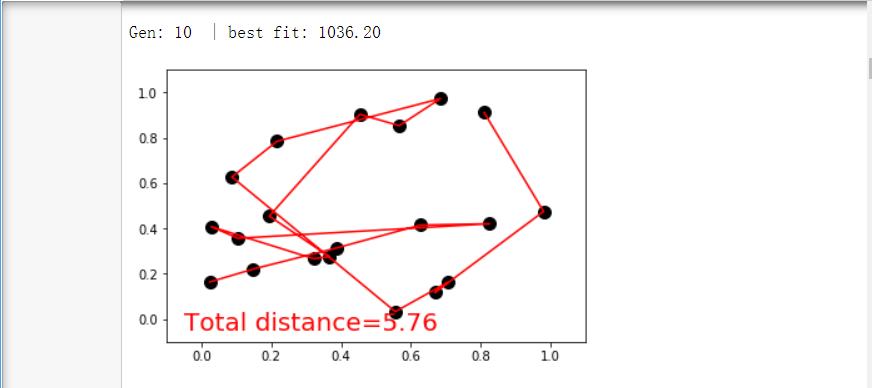
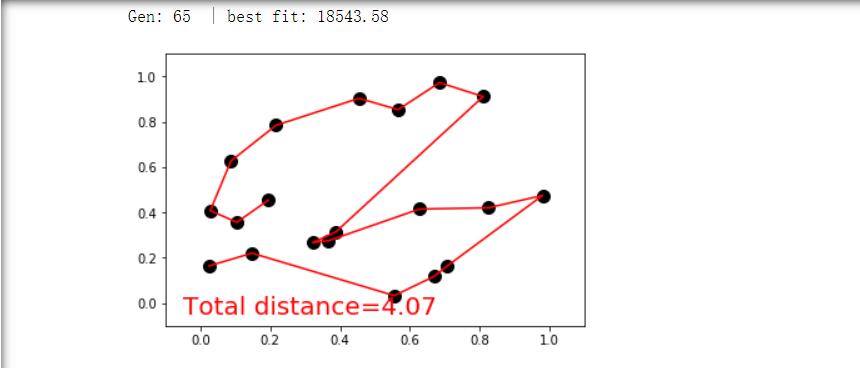
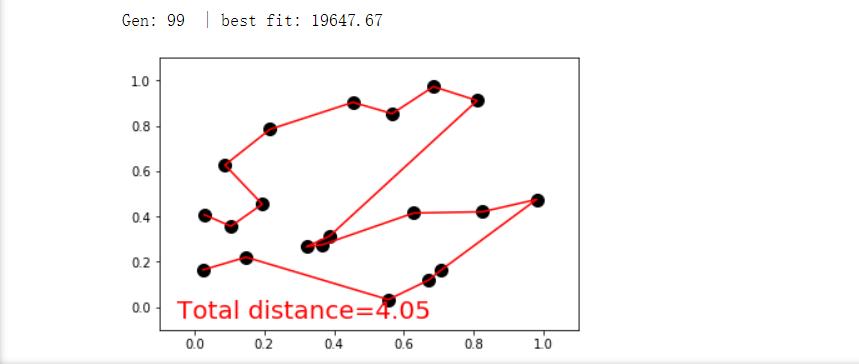
四.结果截图

初始情况（进行100次迭代）：