红黑树(Red-Black Tree)图文解析
Posted queuelovestack
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了红黑树(Red-Black Tree)图文解析相关的知识,希望对你有一定的参考价值。
文章目录
红黑树简介
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它是一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
(1)每个节点要么是黑色,要么是红色。
(2)根节点为黑色
(3)每个叶子节点(NIL)均为黑色。[注:这里的叶子节点指的是空(NIL或者NULL)的叶子节点!!!]
(4)如果一个节点是红色的,那么它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点NIL的所有路径上包含相同数目的黑节点。[注:这里指到叶子节点的路径]
特别说明:
①特性(3)中的叶子节点,指的是只为空(NIL或NULL)的节点。
②特性(5),确保没有一条路径会比其他路径长出两倍。因为,红黑树是相对接近平衡二叉树。
红黑树示意图如下:
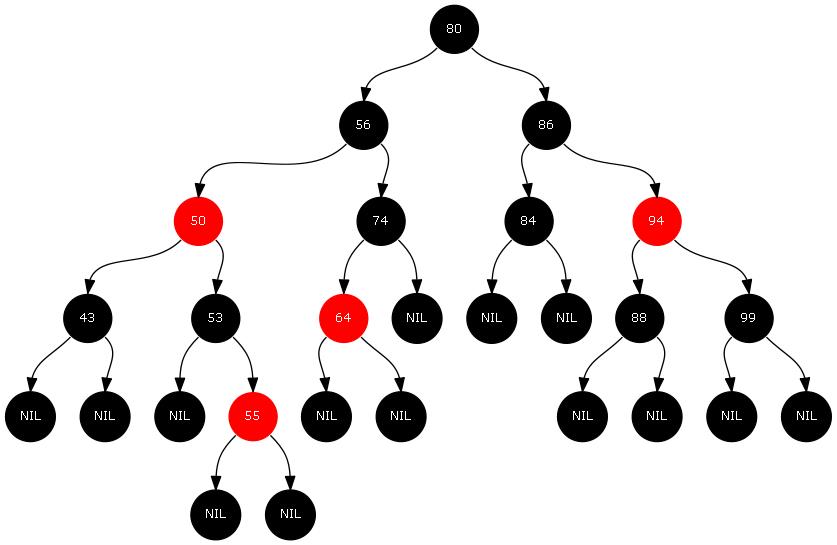
红黑树的应用
红黑树的应用十分广泛,以至于我们多多少少了解一些总是有好处的。红黑树可以用来储存有序数据[1],时间复杂度是O(logn),效率非常高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树实现的。
红黑树的基本操作——左旋和右旋
红黑树虽然特殊,但它也是一种树类型的数据结构,少不了增删查这类的操作。但在介绍添加、删除之前,我们需要先介绍一下旋转操作,这主要是出于对红黑树特性的考虑。毕竟在删除或者添加节点之后,很有可能会破坏原有的红黑树结构特性,这时候旋转操作就必不可少了,这和AVL树有一点点相像。总而言之,旋转的目的是让树保持红黑树的特性。
旋转包含两种:左旋和右旋。下面会分别进行介绍。
1.左旋
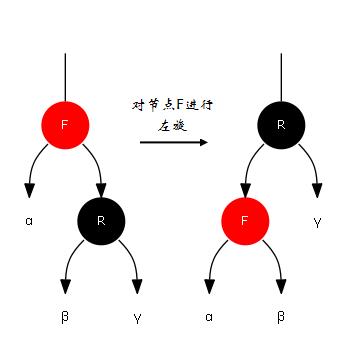
对节点F进行左旋,意味着将节点F变为其右孩子节点R的左孩子节点,并将节点R的左子树变为节点F的右子树。可参考下图进行理解(此处暂时忽略节点的颜色问题):
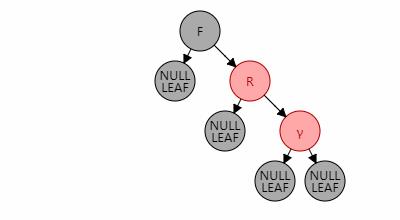
对左旋稍微有点概念之后,可以结合伪代码进行理解“如何对节点x进行左旋”。
LEFT-RORATE(T, x)
y ← right[x] //前提条件: 假设x的右孩子是y。下面开始正式操作
right[x] ← left[y] //将 “y的左孩子” 设为 “x的右孩子”,即 将β设为F的右孩子
p[left[y]] ← x //将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为F
p[y] ← p[x] //将 “x的父亲” 设为 “y的父亲”
if p[x] = nil[T]
then root[T] ← y //情况1: 如果 “x的父亲” 是空节点,则将y设为根节点
else if x = left[p[x]]
then left[p[x]] ← y //情况2: 如果x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
else right[p[x]] ← y //情况3: (x是它父节点的右孩子) 将y设为 “x的父节点的右孩子”
left[y] ← x //将 “x” 设为 “y的左孩子”
p[x] ← y //将 “x的父节点” 设为 “y”
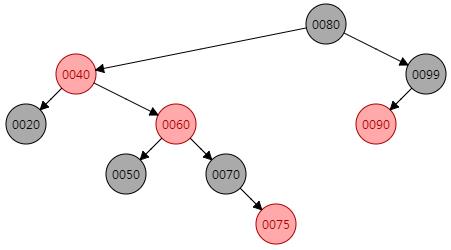
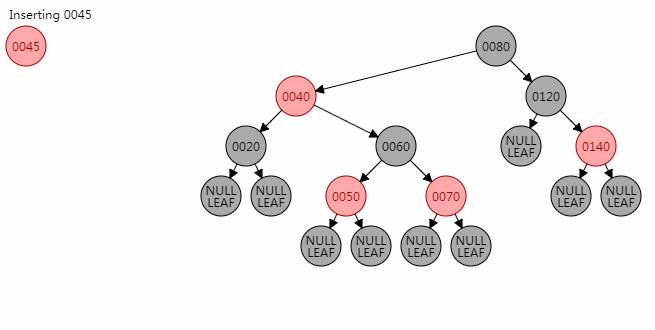
理解左旋之后,不妨进行一个小测验吧,如下图所示是红黑树操作过程的某个状态,现在我们要对节点0040进行左旋,自己动手尝试一下吧,答案点这里哟[2]。
2.右旋
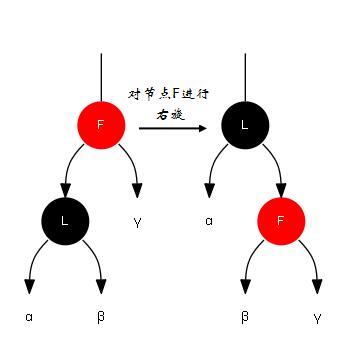
对节点F进行右旋,意味着将节点F变为其左孩子节点L的右孩子节点,并将节点L的右子树变为节点F的左子树。
对右旋稍微有点概念之后,可以结合伪代码进行理解“如何对节点x进行右旋”。
RIGHT-RORATE(T, x)
y ← left[x] //前提条件: 假设x的左孩子是y。下面开始正式操作
left[x] ← right[y] //将 “y的右孩子” 设为 “x的左孩子”,即 将β设为F的左孩子
p[right[y]] ← x //将 “x” 设为 “y的右孩子的父亲”,即 将β的父亲设为F
p[y] ← p[x] //将 “x的父亲” 设为 “y的父亲”
if p[x] = nil[T]
then root[T] ← y //情况1: 如果 “x的父亲” 是空节点,则将y设为根节点
else if x = left[p[x]]
then left[p[x]] ← y //情况2: 如果x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
else right[p[x]] ← y //情况3: (x是它父节点的右孩子) 将y设为 “x的父节点的右孩子”
right[y] ← x //将 “x” 设为 “y的右孩子”
p[x] ← y //将 “x的父节点” 设为 “y”
理解右旋之后,同样进行一个小测验,如下图所示是红黑树操作过程的某个状态,现在我们要对节点0040进行左旋,自己动手尝试一下吧,答案点这里哟[3]。

旋转总结:
⒈左旋 和 右旋 是相对应的两个概念(比较一下就会发现),理解了一个,另一个自然信手拈来。


⒉左旋示例图(以x为节点进行左旋):
z
x /
/ \\ --(左旋)--> x
y z /
y
对x进行左旋,意味着将“x的右孩子”设为“x的父亲节点”;即,将 x变成了一个左节点(x成了为z的左孩子)。因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
⒊右旋示例图(以x为节点进行右旋):
y
x \\
/ \\ --(右旋)--> x
y z \\
z
对x进行右旋,意味着将“x的左孩子”设为“x的父亲节点”;即,将 x变成了一个右节点(x成了为z的右孩子)。因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
红黑树的基本操作——添加
将一个节点插入到红黑树中,需要执行哪些步骤呢? ⑴首先,红黑树是一棵二叉查找树,节点插入规则是插入的数若小于当前节点,则往左子树深入,否则往右子树深入;⑵然后,将插入的节点着色为红色;⑶最后,通过旋转和重新着色操作来修正该树的红黑树特性。详细步骤如下:
第一步:将节点按照二叉查找树的插入规则进行节点插入。
红黑树本身就是一棵二叉查找树,将节点插入后,该树仍然是一颗二叉查找树。也就意味着,树的键值仍然是有序的。此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。这也就意味着,任何的旋转和重新着色操作,都不会改变它仍然是一棵二叉查找树的事实。
好了,那接下来,我们就想方设法通过旋转以及重新着色,使这棵树重新成为红黑树即可。
第二步:将插入节点着色为红色。
为什么着色成红色,而不是黑色呢?在回答之前,我们需要重新温习一下红黑树的特性:
(1)每个节点要么是黑色,要么是红色。
(2)根节点为黑色
(3)每个叶子节点(NIL)均为黑色。[注:这里的叶子节点指的是空(NIL或者NULL)的叶子节点!!!]
(4)如果一个节点是红色的,那么它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点NIL的所有路径上包含相同数目的黑节点。[注:这里指到叶子节点的路径]
将插入的节点着色为红色,不会违背“特性⑸”。少违背一条特性,就意味着我们需要处理的情况越少。接下来,只要努力让这棵树满足其它性质即可。都满足了的话,它就又是一棵红黑树了。
第三步:通过旋转和重新着色操作来修正该树的红黑树特性。
第二步中,将插入节点着色为“红色”之后,不会违背“特性⑸”。那它到底会违背哪些特性呢?
对于“特性⑴”,显然不会违背,因为我们已经将它涂成红色了。
对于“特性⑵”,显然也不会违背。在第一步中,我们是按二叉查找树的规则执行的插入操作,而根据二叉查找树的特点,插入操作不会改变根节点。所以,根节点仍然是黑色。
对于“特性⑶”,显然不会违背。因为这里的叶子节点指的是空叶子节点,插入非空节点并不会对它们造成影响。
对于“特性⑷”,是有可能违背的。
这样分析下来,我们只要满足了“特性⑷”就可以将树重新构造成红黑树了。
接下来我们一起来看一下伪代码,随后会对各种情况进行分析。
添加操作的伪代码
RB-INSERT(T, z)
x ← root[T] //设“红黑树T”的根节点为“x”
y ← nil[T] //新建节点“y”,将y设为空节点,这里的y是作为x的父节点使用的
while x ≠ nil[T] //当“x”指向空叶子节点时,意味着找到了要插入节点“z”在红黑树T中的父节点“y”
do y ← x
if key[z] < key[x]
then x ← left[x]
else x ← right[x]
p[z] ← y //设置“z”的父节点是“y”
if y = nil[T]
then root[T] ← z //情况1: 若y是空节点,则设“z”为根,因为y是x的父节点,且只有x是根节点的时候,y才是空节点
else if key[z] < key[y]
left[y] ← z //情况2: 若 “z的值” < “y的值”,则设“z”为“y”的左孩子
else right[y] ← z //情况3: 若 “z的值” ≥ “y的值”,则设“z”为“y”的右孩子
left[z] ← nil[T] //“z”的左孩子设为空节点
right[z] ← nil[T] //“z”的右孩子设为空节点,到这一步已经完成了“将z节点插入到红黑树中”的操作
color[z] ← RED //将“z”着色为红色
RB-INSERT-FIXUP(T, z) //通过RB-INSERT-FIXUP对红黑树的节点进行重新着色以及旋转,让树T仍然保持红黑树特性
结合伪代码及注释,先理解RB-INSERT节点插入过程。之后,我们对节点重新着色和旋转操作进行说明。
添加修正操作的伪代码
RB-INSERT-FIXUP(T, z)
while color[p[z]] = RED //若当前节点“z”的父节点是红色,则进行以下处理
do if p[z] = left[p[p[z]]] //若“z的父节点”是“z的祖父节点”的左孩子,则进行以下处理
then y ← right[p[p[z]]] //将“y”设置成“z”的叔叔节点(z的祖父节点的右孩子)
if color[y] = RED //Case1: “叔叔节点”是红色
then color[y] ← BLACK ▲ case1 // ①将“叔叔节点”设置为黑色
color[p[z]] ← BLACK ▲ case1 // ②将“父亲节点”设置为黑色
color[p[p[z]]] ← RED ▲ case1 // ③将“祖父节点”设置为红色
z ← p[p[z]] ▲ case1 // ④将“祖父节点”设置为“当前节点”(红色节点)[红色节点是要继续处理的]
else
if z = right[p[z]] //Case2: “叔叔节点”是黑色,且当前节点是右孩子
then z ← p[z] ▲ case2 // ①将“父节点”设置为“新的当前节点”
LEFT-RORATE(T, z) ▲ case2 // ②以“新的当前节点”为支点进行左旋
//Case3: “叔叔节点”是黑色,且当前节点是左孩子
color[p[z]] ← BLACK ▲ case3 // ①将“父亲节点”设置为黑色
color[p[p[z]]] ← RED ▲ case3 // ②将“祖父节点”设置为红色
RIGHT-RORATE(T, p[p[z]]) ▲ case3 // ③以“祖父节点”为支点进行右旋
else (same as then clause with "right" and "left" exchanged) //若“z的父节点”是“z的祖父节点”的右孩子,将上面操作中的“right”和“left”交换位置,然后依次执行即可
color[root[T]] ← BLACK //根节点设置为黑色
根据被插入节点的父节点的情况,可以将“节点z插入红黑树中并着色为红色”划分为三种情况来处理。
㈠情况说明: 被插入节点是根节点。
处理方法: 直接把该节点涂为黑色。
㈡情况说明: 被插入节点的父节点是黑色。
处理方法: 无需处理,节点插入后不影响红黑树特性。
㈢情况说明: 被插入节点的父节点是红色。
处理方法: 该情况与红黑树“特性⑸”冲突。该情况下,被插入节点必定存在非空祖父节点(原因: 被插入节点的父节点是红色,所以必定不是根节点,那么必定有一个黑色的祖父节点)。进一步说明,被插入节点也一定存在叔叔节点(即便叔叔节点是空叶子节点,我们也认为存在,因为空叶子节点本身就是黑色)。理解这点之后,我们又可以根据叔叔节点的情况进一步划分出三种情况(Case)。
| 现象说明 | 处理策略 | |
|---|---|---|
| Case1 | 当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色 | 1.将“父节点”设为黑色 2.将“叔叔节点”设为黑色 3.将“祖父节点”设为红色 4.将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作 |
| Case2 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子 | 1.将“父节点”作为“新的当前节点” 2.以“新的当前节点”为支点进行左旋 |
| Case3 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子 | 1.将“父节点”设为黑色 2.将“祖父节点”设为红色 3.以“祖父节点”为支点进行右旋 |
注:此表仅考虑被插入节点的父节点为祖父节点的左孩子的情况,另一种情况与之对称。
以上三种情况处理问题的核心思想都是: 将红色节点移到根节点;然后将根节点设为黑色。下面将进行详细介绍。
1.(Case 1)叔叔节点是红色
1.1 现象说明
当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色
1.2 处理策略
⑴将“父节点”设为黑色
⑵将“叔叔节点”设为黑色
⑶将“祖父节点”设为红色
⑷将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作
下面分析一下为什么要这样处理(建议结合示意图进行理解):
“当前节点”和“父节点”都是红色,违背“特性⑷”。所以,将“父节点”染成“黑色”这点毋庸置疑。
但是,将“父节点”由“红色”染成“黑色”之后,违背了“特性⑸”:因为,包含“父节点”的这条分支的黑色节点总数增加了1。 解决这个问题的办法是:将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”。关于这里,说明几点:第一,为什么“祖父节点”之前是黑色?这个应该很容易想明白,因为在变换操作之前,该树是红黑树,“父节点”是红色,那么“祖父节点”一定是黑色; 第二,为什么将“祖父节点”由“黑色”变成“红色”,同时,将“叔叔节点”由“红色”变成“黑色”?因为这样能解决“包含‘父节点’的分支的黑色节点总数增加了1”的问题。这个道理也很简单。“包含‘父节点’的分支的黑色节点总数增加了1” 同时也意味着 “包含‘祖父节点’的分支的黑色节点的总数增加了1”,既然这样,我们通过将“祖父节点”由“黑色”变成“红色”以解决“包含‘祖父节点’的分支的黑色节点的总数增加了1”的问题; 但是,这样处理之后又会引起另一个问题“包含‘叔叔’节点的分支的黑色节点的总数减少了1”,现在我们已知“叔叔节点”是“红色”,将“叔叔节点”设为“黑色”就能解决这个问题。 所以,将“祖父节点”由“黑色”变成“红色”,同时,将“叔叔节点”由“红色”变成“黑色”,就解决了该问题。
按照上面的步骤处理之后:当前节点、父节点、叔叔节点之间都不会违背红黑树特性,但祖父节点却不一定。若此时,祖父节点是根节点,直接将祖父节点设为“黑色”,那就完全解决这个问题了;若祖父节点不是根节点,那我们需要将“祖父节点”设为“新的当前节点”,接着对“新的当前节点”进行分析。
1.3 示意图
1.3.1 动图演示
1.3.2 过程模拟
第一步:
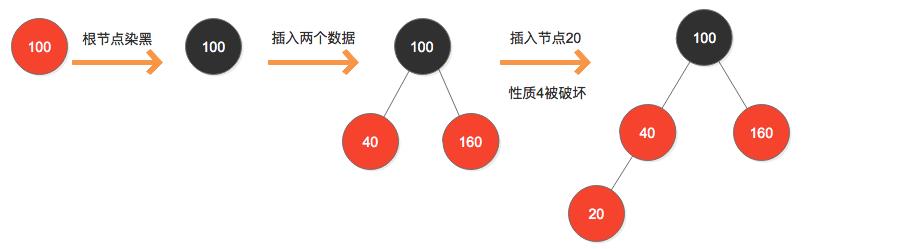
第二步:修复操作(当前节点是20,用cur表示)
第三步:继续对新的当前节点进行修复操作
这里因为到达了根节点,所以停止了修复,如果当前节点不是根节点,或者当前节点的父节点不是黑色节点,那么就需要继续向上修复。
第四步:继续插入新节点

第五步:插入新节点–再接再厉
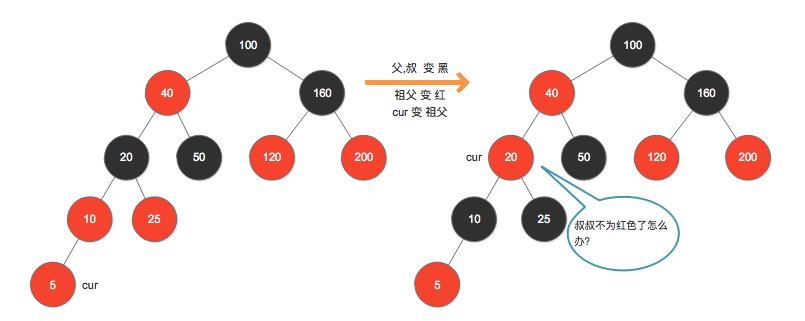
这时候面临的是叔叔节点不是红色,不再满足case1的情况,继续分析。
2.(Case 2)叔叔节点是黑色,且当前节点是右孩子
2.1 现象说明
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子
2.2 处理策略
⑴将“父节点”作为“新的当前节点”
⑵以“新的当前节点”为支点进行左旋
下面分析一下为什么要这样处理(建议结合示意图进行理解):
首先,将“父节点”作为“新的当前节点”;接着,以“新的当前节点”为支点进行左旋。 为了便于理解,我们先说明第⑵步,再说明第⑴步;为了便于说明,我们设置“父节点”的代号为F(Father),“当前节点”的代号为S(Son)。
为什么要“以F为支点进行左旋”呢?其实这里是为case 3这种情况做的准备(可以结合case 3一起理解 or 先理解case 3的策略),我们修复红黑树秉持着能少处理就少处理的原则,但是此处单纯依靠重新染色操作无法避免与“特性⑷”和“特性⑸”相违背,迫于无奈只能采取变动稍大的旋转操作。而此处的左旋是和case 3的右旋相对应的,假设我们没有进行左旋,而是对祖父节点直接进行右旋,那么只是将“违背特性⑷”的问题换了一个分支,但问题依然存在。如下图,当前节点是60,父节点是40,叔叔节点是90,祖父节点是80,若我们不对父亲节点左旋,而是直接采取case 3的操作,就会发现,问题并没有解决,只是把皮球抛给了对方。综上,这也就是这里为什么要“以F为支点进行左旋”的原因。
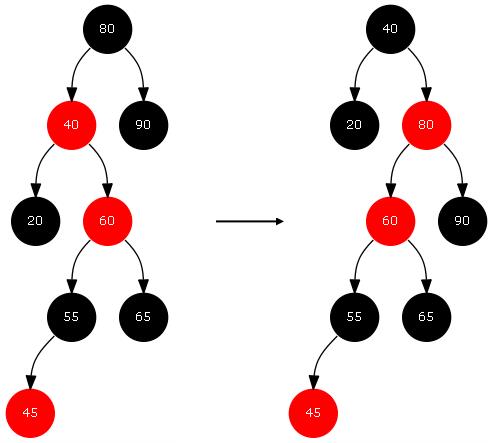
按照上面的步骤(以F为支点进行左旋)处理之后:若S变成了根节点,那么直接将其设为“黑色”,就完全解决问题了;若S不是根节点,那我们需要执行步骤⑴,即“将F设为‘新的当前节点’”。那为什么不继续以S为新的当前节点继续处理,而需要以F为新的当前节点来进行处理呢?这是因为“左旋”之后,F变成了S的“子节点”,即S变成了F的父节点;而我们处理问题的时候,需要从下至上(由叶到根)方向进行处理;也就是说,必须先解决“孩子”的问题,再解决“父亲”的问题;所以,我们执行步骤⑴:将“父节点”作为“新的当前节点”。
2.3 示意图
2.3.1 动图演示
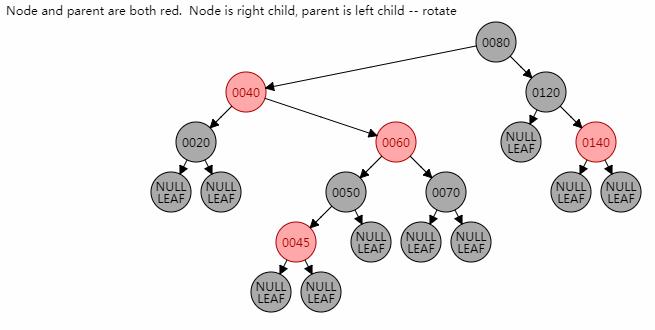
2.3.2 过程模拟
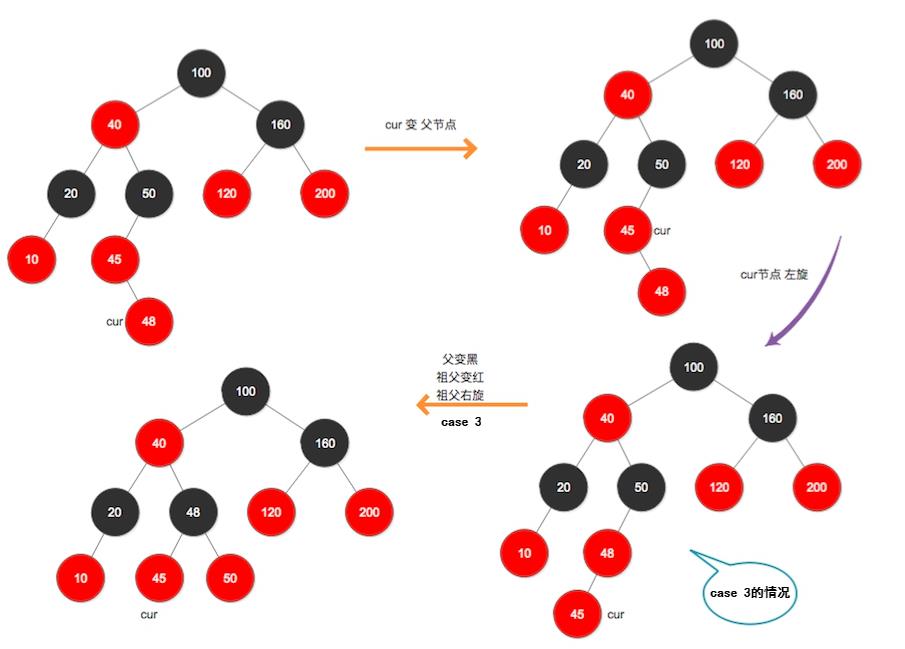
该过程提前剧透了case 3的处理策略,可以先看看。
3.(Case 3)叔叔节点是黑色,且当前节点是左孩子
3.1 现象说明
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子
3.2 处理策略
⑴将“父节点”设为黑色
⑵将“祖父节点”设为红色
⑶以“祖父节点”为支点进行右旋
下面分析一下为什么要这样处理(建议结合示意图进行理解):
为了便于说明,我们设置“当前节点”为S(Son),“叔叔节点”为U(Uncle),“父节点”为F(Father),祖父节点为G(Grand-Father)。
目前,所有分支的黑色节点个数是一致的,现在出现两个连续红色节点S和F,那么简单点,将其中一个改成黑色节点,将父节点F变成黑色,那么以父节点F的局部子树是平衡的,但是 父节点的兄弟节点U可能是不平衡的,因为父节点F路径多了一个黑色,那么这个黑色节点放在哪里? 只能往根节点移,将祖父G变红,这样祖父G的另一个分支将少一个黑色节点,再把祖父G右旋,这样父节点F代替了原来的祖父G,也就相当于把多的黑色节点,放在了公共的祖父位置上。
3.3 示意图
3.3.1 动图演示
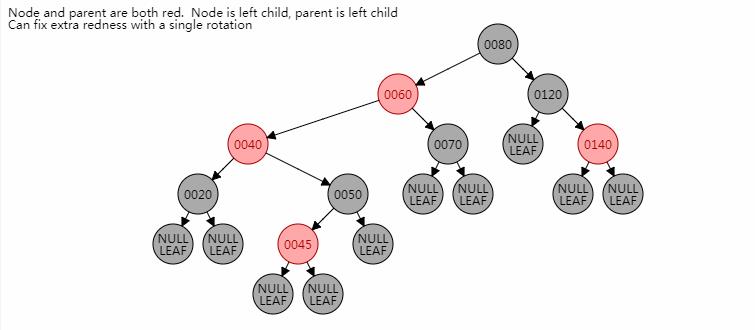
3.3.2 过程模拟

至此,红黑树的添加操作终于完成了。
红黑树的基本操作——删除
将红黑树内的某一个节点删除,需要执行哪些步骤呢? ⑴首先,红黑树是一棵二叉查找树,按照二叉查找树的节点删除规则删除该节点;⑵然后,通过旋转和重新着色操作来修正该树的红黑树特性。详细步骤如下:
第一步:将节点按照二叉查找树的删除规则进行节点删除。
这和“删除常规二叉查找树中的节点方法是一样的”。分3种情况:
Ⅰ.被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
Ⅱ.被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
Ⅲ.被删除节点有两个儿子。那么,先找出它的[前驱节点/后继节点];然后把“它的[前驱节点/后继节点]的内容”复制给“该节点”;之后,删除“它的[前驱节点/后继节点]”。在这里,[前驱节点/后继节点]相当于替身,在将[前驱节点/后继节点]的内容复制给"被删除节点"之后,再将[前驱节点/后继节点]删除。这样就巧妙的将问题转换为“删除[前驱节点/后继节点]”的情况了,下面就考虑[前驱节点/后继节点]。在"被删除节点"有两个非空子节点的情况下,它的[前驱节点/后继节点]不可能是双子非空。既然"[前驱节点/后继节点]"不可能双子都非空,就意味着"该节点的[前驱节点/后继节点]"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况Ⅰ"进行处理;若只有一个儿子,则按"情况Ⅱ"进行处理。
第二步:通过旋转和重新着色操作来修正该树的红黑树特性。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
接下来我们一起来看一下伪代码,随后会对各种情况进行分析。
删除操作的伪代码
RB-DELETE(T, z)
if left[z] = nil[T] or right[z] = nil[T]
then y ← z //若 “z的左孩子” 或者 “z的右孩子” 为空,则将“z”赋值给“y”
else y ← TREE-PRECURSOR(z) //否则,将“z的前驱节点”赋值给“y”,或将“z的后继节点”赋值给“y”,y ← TREE-SUCCESSOR(z)
if left[y] ≠ nil[T]
then x ← left[y] //若 “y的左孩子” 不为空,则将“y的左孩子”赋值给“x”
else x ← right[y] //否则将“y的右孩子”赋值给“x”
p[x] ← p[y] //将“y的父节点”设置为“x的父节点”
if p[y] = nil[T]
then root[T] ← x //情况1: 若“y的父节点”为空,则设置“x”为根节点
else if y = left[p[y]]
then left[p[y]] ← x //情况2: 若“y是它父节点的左孩子”,则设置“x”为“y的父节点”的左孩子
else right[p[y]] ← x //情况3: 若“y是它父节点的右孩子”,则设置“x”为“y的父节点”的右孩子
if key[y] ≠ key[z]
then key[z] ← key[y] //若“y的值”和“z的值”不等,则赋值给“z”。注意: 这里只拷贝z的值给y,而没有拷贝z的颜色
if color[y] = BLACK
then RB-DELETE-FIXUP(T, x) //若“y为黑节点”,则需要进行染色、旋转修正
return y //返回删除节点用于delete(C++实现时需要)
结合伪代码及注释,先理解RB-DELETE节点删除过程。之后,我们对节点重新着色和旋转操作进行说明。
删除修正操作的伪代码
RB-DELETE-FIXUP(T, x)
while x ≠ root[T] and color[x] = BLACK //若“x”是红节点或根节点,直接染成黑色即可
do if x = left[p[x]]
then w ← right[p[x]] //若 “x”是“它父节点的左孩子”,则设置 “w”为“x的兄弟”(即w为x父节点的右孩子)
if color[w] = RED //Case 1: x是“黑”节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)
then color[w] ← BLACK ▲ case1 // ①将“兄弟节点”设置为黑色
color[p[x]] ← RED ▲ case1 // ②将“父亲节点”设置为红色
LEFT-RORATE(T, p[x]) ▲ case1 // ③以“父亲节点”为支点进行左旋
w ← right[p[x]] ▲ case1 // ④左旋后,重新设置x的兄弟节点
if color[left[w]] = BLACK and color[right[w]] = BLACK //Case 2: x是“黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色
then color[w] ← RED ▲ case2 // ①将“兄弟节点”设置为红色
x ← p[x] ▲ case2 // ②将“父亲节点”设置为“新的x节点”
else
if color[right[w]] = BLACK //Case 3: x是“黑”节点,x的兄弟节点是黑色,x的兄弟节点的左孩子是红色,右孩子是黑色
then color[w] ← RED ▲ case3 // ①将“兄弟节点”设置为红色
color[left[w]] ← BLACK ▲ case3 // ②将“兄弟节点的左孩子”设置为黑色
RIGHT-ROTATE(T, w) ▲ case3 // ③以“兄弟节点”为支点进行右旋
w ← right[p[x]] ▲ case3 // ④右旋后,重新设置x的兄弟节点
//Case 4: x是“黑”节点,x的兄弟节点是黑色,x的兄弟节点的右孩子是红色
color[w] ← color[p[x]] ▲ case4 // ①将“父亲节点”的颜色赋值给“兄弟节点”
color[p[x]] ← BLACK ▲ case4 // ②将“父亲节点”设置为黑色
color[right[w]] ← BLACK ▲ case4 // ③将“兄弟节点的右孩子”设置为黑色
LEFT-RORATE(T, p[x]) ▲ case4 // ④以“父亲节点”为支点进行左旋
x ← root[T] ▲ case4 // ⑤设置“x”为根节点
else (same as then clause with "right" and "left" exchanged) //若 “x”是“它父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行
color[x] ← BLACK
在对删除函数进行分析之前,我们再来温习一遍红黑树的几个特性:
(1)每个节点要么是黑色,要么是红色。
(2)根节点为黑色
(3)每个叶子节点(NIL)均为黑色。[注:这里的叶子节点指的是空(NIL或者NULL)的叶子节点!!!]
(4)如果一个节点是红色的,那么它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点NIL的所有路径上包含相同数目的黑节点。[注:这里指到叶子节点的路径]
前面我们将"删除红黑树中的某个节点"大致分为两步,在第一步中"按照二叉查找树的节点删除规则删除该节点"后,可能违反"特性⑵、⑷、⑸"三个特性。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。
通过RB-DELETE算法,我们知道:删除节点y之后,x占据了原来节点y的位置。那么,我们面临几种形态:
a)节点y为红色
这时我们无需做任何处理,因为并未违反任何一条特性
b)节点y为黑色,x为红色
此时,在删除节点y之后,我们违背了特性⑸,y所在的子树少了一个黑色节点,那我们只需要将x染为黑色补上缺掉的这个黑色节点即可
c)节点y为黑色,x为黑色,但x是根节点
这意味着原来的y就是根节点,这样相当于是所有路径共同减少一个黑色节点,依旧满足红黑树特性,故无需处理
d)节点y为黑色,x为黑色,x不是根节点
这种形态还需要细分四种子情况进行分析:
| 现象说明 | 处理策略 | |
|---|---|---|
| Case1 | 当前节点x是黑色,当前节点的兄弟节点是红色(此时x的父节点和x的兄弟节点的子节点都是黑色) | 1.将“兄弟节点”设为黑色 2.将“父亲节点”设为红色 3.以“父亲节点”为支点进行左旋 4.左 以上是关于红黑树(Red-Black Tree)图文解析的主要内容,如果未能解决你的问题,请参考以下文章 |