区块链之加解密算法&数字证书
Posted LEVI_104
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了区块链之加解密算法&数字证书相关的知识,希望对你有一定的参考价值。
目录
AES(Advanced EncryptionStandard)
DSA(Digital SignatureAlgorithm)
ECC(Elliptic CurvesCryptography)
一.加解密算法
加密简单而言就是通过一种算法将明文信息转换成密文信息,信息的的接收方能够通过密钥对密文信息进行解密获得明文信息的过程。根据加解密的密钥是否相同,算法可以分为对称加密、非对称加密、对称加密和非对称加密的结合。
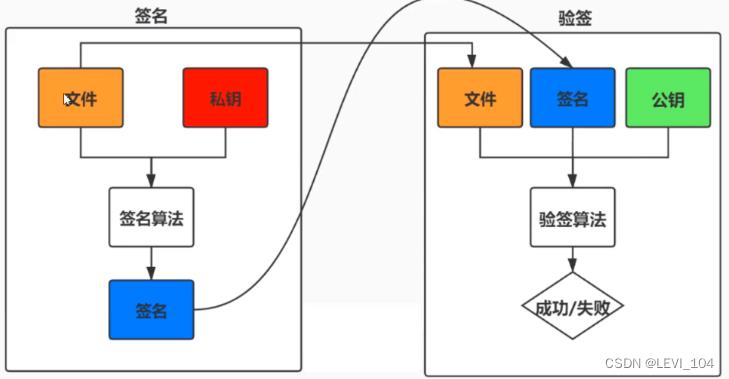
数字签名
数字签名的基本原理就是用私钥去签名,而用公钥去验证签名
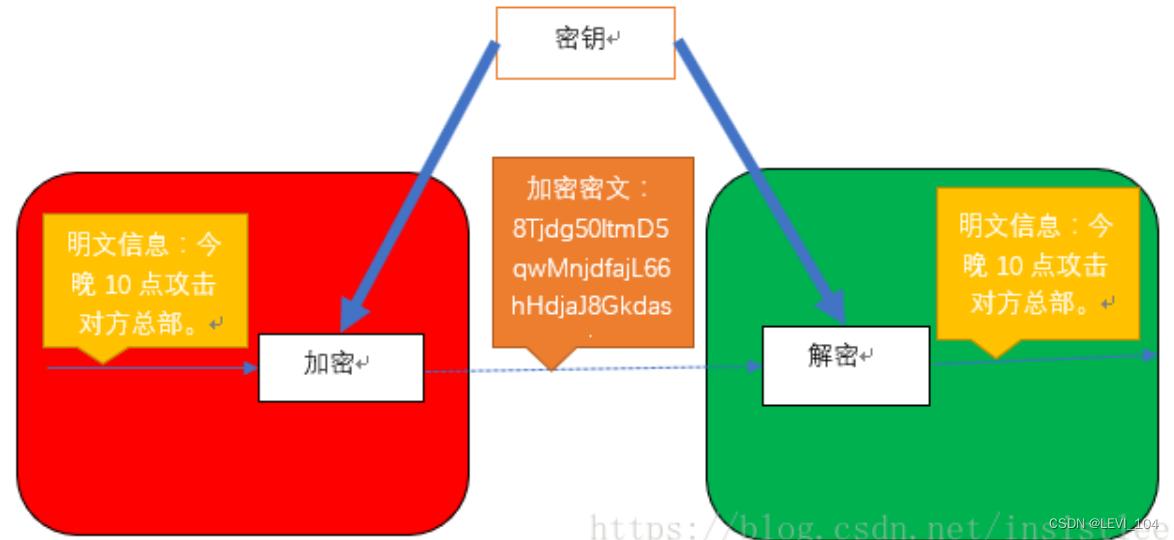
对称加密
对称加密顾名思义就是加密和解密的密钥是相同的
DES(Data EncryptionStandard)
数据加密标准,速度较快,适用于加密大量数据的场合.经典的分组加密算法,1977年由美国联邦信息处理标准(FIPS)采用FIPS-46-3,将64位明文加密为64位的密文,其密钥长度为64位(包含8位校验位)。现在已经很容易被暴力破解
3DES(Triple DES)
基于DES,对一块数据用三个不同的密钥进行三次加密,强度更高.但现在也被认为不够安全;
AES(Advanced EncryptionStandard)
AES也为分组密码,分组密码也就是把明文分成一组一组的,每组长度相等,每次加密一组数据,直到加密完整个明文。 在AES标准规范中,分组长度只能是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的分组长度可以使用128位、 192位或256位。密钥的长度不同,推荐加密轮数也不同。AES的优势在于处理速度快,整个过程可以用数学描述,目前尚未有有效的破解手段;
RSA加密法
RSA 公司发明,是一个支持变长密钥的公共密钥算法,需要加密的文件块的长度也是可变的
DSA(Digital SignatureAlgorithm)
数字签名算法,是一种标准的DSS(数字签名标准),严格来说不算加密算法
ECC(Elliptic CurvesCryptography)
椭圆曲线密码编码学.ECC和RSA相比具有多方面的绝对优势,主要有:抗攻击性强.相同的密钥长度,其抗攻击性要强很多倍.计算量小,处理速度快.ECC总的速度比RSA、DSA要快得多.存储空间占用小.ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多,意味着它所占的存贮空间要小得多.这对于加密算法在IC卡上的应用具有特别重要的意义.带宽要求低.当对长消息进行加解密时,三类密码系统有相同的带宽要求,但应用于短消息时ECC带宽要求却低得多.带宽要求低使ECC在无线网络领域具有广泛的应用前景
现代备受关注的算法系列,基于对椭圆曲线上特定点进行特殊乘法逆运算难以计算的特性。最早在1985年由Neal Koblitz和Victor Miller分别独立提出。ECC系列算法一般被认为具备较高的安全性,但加解密计算过程往往比较费时;
非对称加密
非对称加密算法中,加密密钥和解密密钥是不同的,分别称为公钥(public key)和私钥(private key)。私钥一般需要通过随机数算法生成,公钥可以根据私钥生成。公钥一般是公开的,他人可获取的;私钥一般是个人持有,他人不能获取。
目前普遍认为RSA类算法可能在不远的将来被破解,一般推荐可采用安全强度更高的椭圆曲线系列算法,ECC将会是今后最重要的主流公钥加密技术。
签名与加密过程
签名是用私钥来完成的,用公钥来验签。加密是用公钥来加密,私钥来解密的。为什么会需要签名呢?
需要两个密钥来进行加密和解密,公开密钥(public key,简称公钥)和私有密钥(private key,简称私钥) ,公钥加密的信息只有私钥才能解开,私钥加密的信息只有公钥才能解开。这个公钥和私钥必须是一对的,如果用公钥对数据进行加密,那么只有使用对应的私钥才能解密,所以只要私钥不泄露,那么我们的数据就是安全的。
我们先假设A给B发送信息,A拥有自己的私钥(PRI_A)和公钥(PUB_A),B拥有自己的私钥(PRI_B)和公钥(PUB_B)。 B接收到消息,要怎样才能知道消息是谁发出的。或者换句话说,A发出一则消息,要怎样让接收方知道是A发出的。这时就需要A用PRI_A对信息进行签名,相当于生成了唯一的身份证。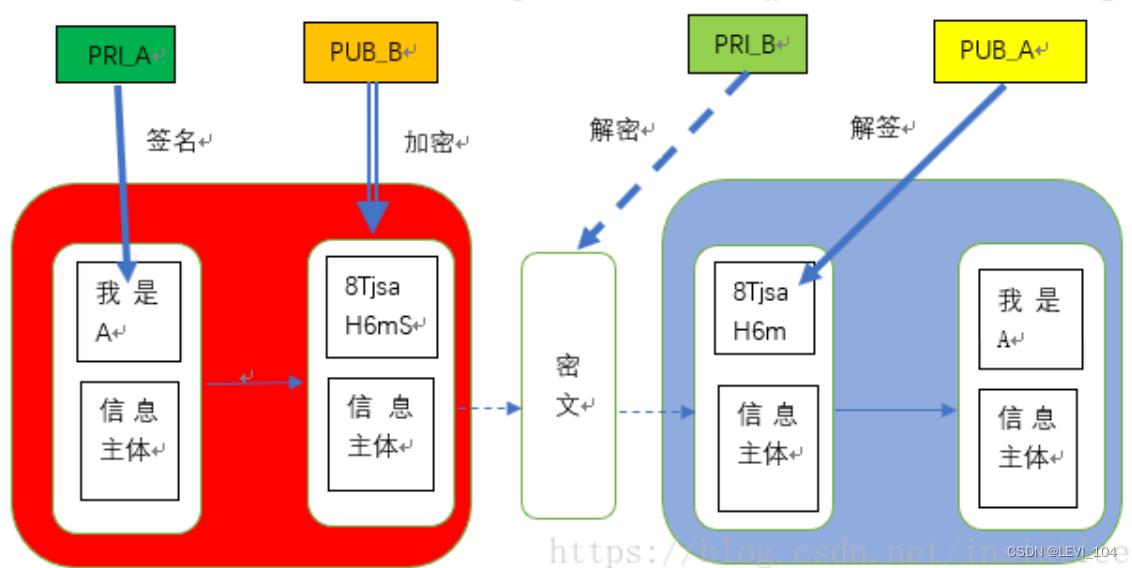
可以这样描述以上图示过程,A向B发送信息的整个签名和加密的过程:
- A先用自己的私钥(PRI_A)对信息(一般是信息的摘要)进行签名;
- A接着使用B的公钥(PUB_B)对信息内容和签名信息进行加密。
这样当B接收到A的信息后,获取信息内容的过程:
- 用自己的私钥(PRI_B)解密A用B的公钥(PUB_B)加密的内容;
- 得到解密后的明文后用A的公钥(PUB_A)解签A用A自己的私钥(PRI_A)的签名。
注意,公钥是公开出去的,但是私钥只能是自己拥有。以上图示过程和签名加密机制保证了端到端的唯一确认。A的签名只有A的公钥才能解签,这样B就能确定是A发出的信息;A的加密只有B的私钥才能解密,因为是用B的公钥加密的,这样保证了信息只能被B读取。
非对称加密的应用
应用最广泛的是银行,银行把每个人的私钥存储在每个人的U盾里,这就相当于,只有解密方自己拥有自己的私钥,银行用你设置的公钥对你的账户进行加密,要解密必须用到自己U盾里的私钥。这就是非对称加密的广泛使用原理。
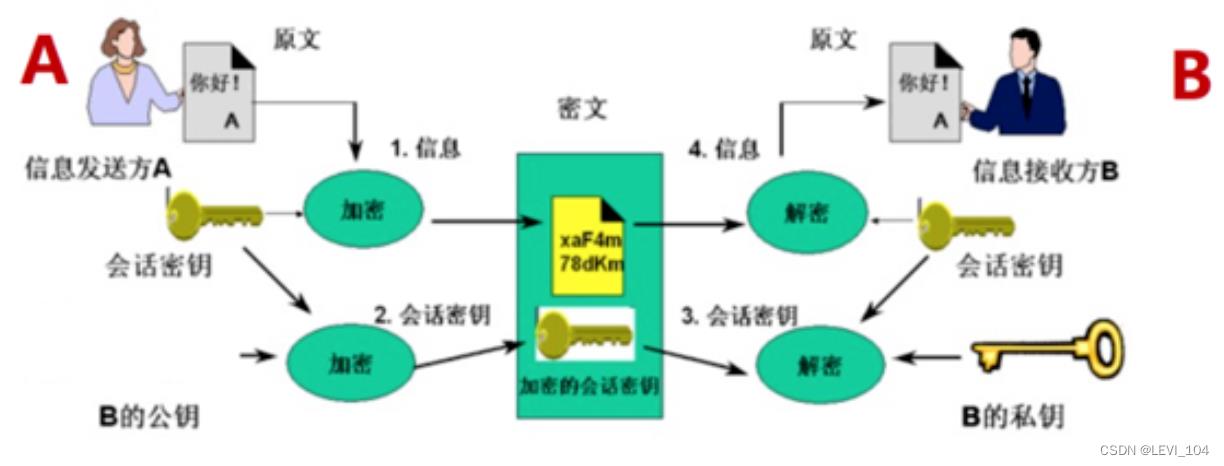
对称加密与非对称加密的结合
这种结合方式分为两个阶段,阶段一利用非对称加密对密钥进行加密传递给接收方,阶段二利用对称加密对明文信息进行加解密。如下图所示:
二.数字证书
图解
(1)鲍勃有两把钥匙:一把是公钥,一把是私钥

(2)鲍勃把公钥送给了他的朋友:帕蒂,道格,苏珊

(3)苏珊要给鲍勃写一封保密的信。她写完后用鲍勃的公钥加密,就可以达到保密效果

(4)鲍勃收到信后,用私钥解密,就看到信件的内容。这里要强调的是,只要鲍勃的私钥不泄露,这封信就是安全的,即使落在别人手里,也无法解密

(5)鲍勃给苏珊回信,决定采用“数字签名”。他写完后,先用Hash函数,生成信件的摘要(digest)

(6)鲍勃将这个签名,附在信件下面,一起发给苏珊
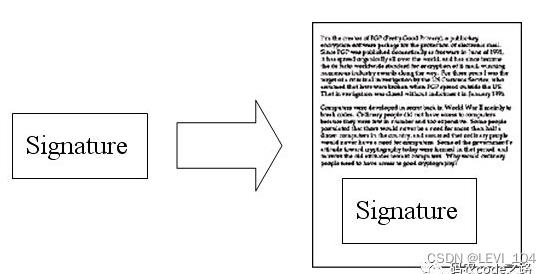
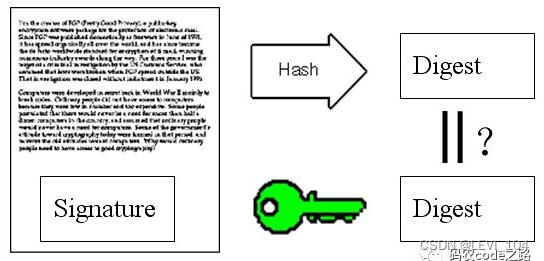
(7)苏珊收到信后,取下数字签名,用鲍勃的公钥解密,得到信件的摘要。由此证明,这封信确实是鲍勃发出的

(8)苏珊再对信件本身使用Hash函数,将得到的结果,与上一步得到的摘要进行对比。如果两者一致,就证明这封信没被修改过
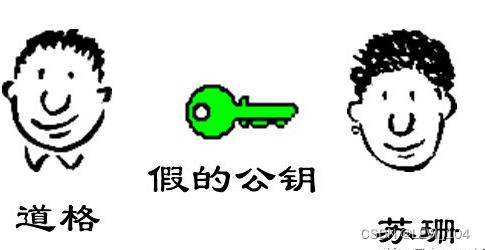
(9)复杂的情况出现了:道格想要欺骗苏珊,他偷偷地使用了苏珊的电脑,用自己的公钥换走了鲍勃的公钥。此时,苏珊实际上拥有的是道格的公钥,但是她还认为这是鲍勃的公钥。因此,道格可以冒充鲍勃,用自己的私钥做成“数字签名”,发信给苏珊,让苏珊用假的鲍勃公钥进行解密
(10)后来,苏珊感觉不对劲,发现自己无法确定公钥是否真的属于鲍勃。她想到了一个办法,要求鲍勃去找“证书中心CA”,为公钥做认证。证书中心用自己的私钥,对鲍勃的公钥和一些相关信息一起加密,生成“数字证书”
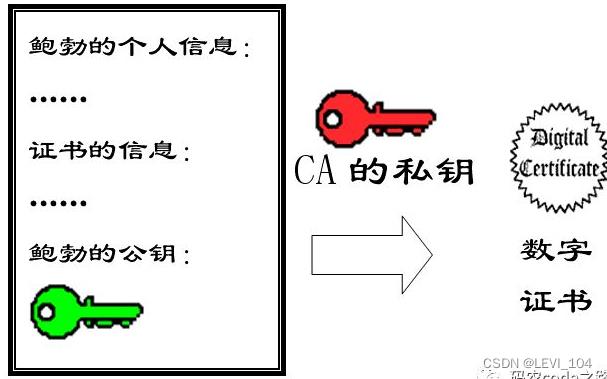
(11)鲍勃拿到数字证书后,就可以放心了。以后再给苏珊写信,只要在签名的同时,附上数字证书就可以了

(12)苏珊收到信后,用CA的公钥解开数字证书,就可以拿到鲍勃真实的公钥了,然后就可以证明“数字签名”是否真的属于鲍勃
详细了解数字证书,查看维基百科:https://zh.wikipedia.org/wiki/%E5%85%AC%E9%96%8B%E9%87%91%E9%91%B0%E8%AA%8D%E8%AD%89
区块链之哈希算法(完整篇)
读过我之前的文章或者对比特币比较了解的同学应该都清楚像比特币这些数字货币必然离不开密码学。而比特币中用到的密码学主要是哈希算法和数字签名。今天就给大家普及一下哈希算法。
哈希算法是基于密码学中的哈希函数。哈希函数主要有下面几个特征:
输入可以是任何长度和大小的字符串。
输出是固定长度的。在比特币中输出固定为256位。
它能在一定的时间内输出结果。时间复杂度为O(N).
哈希函数之所以可以用于加密,主要是它具有三个特性:
碰撞阻力
隐秘性
谜题友好
碰撞阻力 密码学中的碰撞是指对于两个不同的输入,产生相同的输出。而哈希函数中的碰撞阻力就是指如果想找到两个不同的输入,产生相同的输出,是有一定的难度的。但并不是不可以,你可以试想对于哈希函数,输入是无限时,输出是有限长度的,所以必然会存在多个不同的输入产生相同的输出。但要想找到两个不同的输入产生相同的输出是要花费很大的精力和时间。
举个例子,考虑对应于一个256位输出大小的哈希函数, 选择2^256 +1个不同数值, 计算每个数的哈希值, 并检查是否有两个相等的输出。因为我们这里选择的输入多于输出, 因此在应用哈希函数时, 一些数对必将产生碰撞。但对于一个256位输出的哈希函数来说, 最坏的情况是你需要进行2^256 +1次哈希函数计算, 平均次数为2^128 次, 这简直是一个天文数字——如果一台电脑每秒计算10000个哈希值, 计算2^128 个哈希值, 需要花10^27 多年时间! 所以说哈希函数的碰撞阻力是很大的,十分适合于加密。
哈希函数(算法)具有隐秘性,其实它并不“隐秘”,它并不难理解。简单地说,就是如果我们仅仅知道H(x)=H(y),要想反推其中的x和y,我们是需要花巨大的力气。专业的定义是:
隐秘性 哈希函数H具有隐秘性, 如果:当其输入r选自一个高阶最小熵(highmin-entroy) 的概率分布, 在给定H(r‖x) 条件下来确定x是不可行的。
学过信息论的同学应该清楚什么叫熵, 在这里我就不再展开了。所谓的最小熵可以简单地理解为最小值。举个具体的例子, 如果r是从长度为256位的字符串中随意选出的,那么任意特定字符串被选中的概率为1/2^256 , 这是一个小到几乎可以忽略的取值。
想必学到这里,大家应该清楚哈希函数(算法)的隐秘性,最后我还总结一下,哈希函数的隐秘性就是尽管必然存在两个或多个不同输入,使得哈希函数的输出值一样,但要想通过计算找出这些不同的输入是十分的困难的。
最后,哈希函数还具有谜题友好性。
下面先给出传统的定义:
谜题友好 如果对于任意n位输出值y, 假定k选自高阶最小熵分布, 如果无法找到一个可行的方法, 在比2^n 小很多时间内找到x, 保证H(k‖x)=y成立, 那么我们称哈希函数H为谜题友好。
这里同样涉及到信息论中熵的概念,但我并不打算展开讲,因为我认为对于这些概念只要在大体上理解就行,但感兴趣的同学也可以自行百度。其实,所谓的谜题友好,通俗地说就是如果有一个人想找到y值所对应的输入, 假定在输入集合中, 有一部分是非常随机的, 那么他将非常难以求得y值对应的输入。
细心的同学应该都发现了,其实隐秘性和谜题友好都在强调一件事情,知道哈希函数的输出值,来反求其输入值,是十分地困难。隐秘性是从概率的角度强调,能够反求出输入值的概率非常小,谜题友好是从时间的角度强调在很小的时间内是非常难求出其输入值。但它们都有同一个目的,就是反求出其输入值难度是非常地大。
最后,如果一个哈希函数具备谜题友好特性, 这就意味着对于这个谜题没有一个解决策略,比只是随机地尝试x取值会更好。 到这里应该就清楚为什么平时比特币挖矿的很多方法就是简单的遍历了吧,因为整体时间角度考虑,根本就没有一个比随机地尝试求x的所需的时间更快。
今天先分享到此,知识虽不多,但正所谓骐骥一跃,不能十步;驽马十驾,功在不舍。每天与你分享一个区块链小知识,希望你有所收获。
参考:网络文章、知乎、《区块链:技术驱动金融》、《区块链:从数字货币到信用社会》、《区块链:重塑经济与世界》、《区块链革命:比特币底层技术如何改变货币、商业和世界》、《区块链社会:解码区块链全球应用与投资案例》、《区块链:定义未来金融与经济新格局》
往期精彩文章
以上是关于区块链之加解密算法&数字证书的主要内容,如果未能解决你的问题,请参考以下文章