最优化所需基础知识-第一节:范数
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化所需基础知识-第一节:范数相关的知识,希望对你有一定的参考价值。
文章目录
范数:有别于标量,向量和矩阵并不能直接进行大小比较。所以向量范数和矩阵范数给出了一种长度计量方式
一:向量范数
(1)向量范数定义
向量范数(范数):如果满足以下条件,那么就称一个从向量空间 R n \\R^n Rn到实数域 R \\R R的非负函数||▪||为范数
- 正定性:对于所有的 v ∈ R n v\\in \\R^n v∈Rn,有 ∣ ∣ v ∣ ∣ ≥ 0 ||v||\\geq0 ∣∣v∣∣≥0,且 ∣ ∣ v ∣ ∣ = 0 ||v||=0 ∣∣v∣∣=0当且仅当 v = 0 v=0 v=0
- 齐次性:对于所有的 v ∈ R n v\\in \\R^n v∈Rn和 α ∈ R \\alpha \\in \\R α∈R,有 ∣ ∣ α v ∣ ∣ = ∣ α ∣ ∣ ∣ v ∣ ∣ ||\\alpha v||=|\\alpha|||v|| ∣∣αv∣∣=∣α∣∣∣v∣∣
- 三角不等式:对于所有的 v , w ∈ R n v,w\\in \\R^n v,w∈Rn,有 ∣ ∣ v + w ∣ ∣ ≤ ∣ ∣ v ∣ ∣ + ∣ ∣ w ∣ ∣ ||v+w||\\leq||v|| +||w|| ∣∣v+w∣∣≤∣∣v∣∣+∣∣w∣∣
最常用的向量范数即我们所熟知的 p p p范数( p ≥ 1 p \\geq1 p≥1)
∣ ∣ v ∣ ∣ p = ( ∑ i = 1 n ∣ v i ∣ p ) 1 p ||v||_p=(\\sum\\limits_i=1^n|v_i|^p)^\\frac1p ∣∣v∣∣p=(i=1∑n∣vi∣p)p1
- 当 p = ∞ p=\\infty p=∞时, l ∞ l_\\infty l∞范数可定义为 ∣ ∣ v ∣ ∣ ∞ = m a x 1 ≤ i ≤ n ∣ v i ∣ ||v||_\\infty=\\mathopmax\\limits_1\\leq i\\leq n|v_i| ∣∣v∣∣∞=1≤i≤nmax∣vi∣
- 以向量 v = ( x 1 , x 2 , . . . , x n ) T v=(x_1,x_2,...,x_n)^T v=(x1,x2,...,xn)T为例,则有 ∣ ∣ v ∣ ∣ 1 = ∣ x 1 ∣ + ∣ x 2 ∣ + . . . + ∣ x n ∣ ||v||_1=|x_1|+|x_2|+...+|x_n| ∣∣v∣∣1=∣x1∣+∣x2∣+...+∣xn∣、 ∣ ∣ v ∣ ∣ 2 = x 1 2 + x 2 2 + . . . + x n 2 ||v||_2=\\sqrtx_1^2+x_2^2+...+x_n^2 ∣∣v∣∣2=x12+x22+...+xn2
(2)向量范数的意义
向量范数的意义:向量范数度量的是 v v v与零点之间的距离,下图所展示的分别是 ∣ ∣ v ∣ ∣ 1 、 ∣ ∣ v ∣ ∣ 2 、 ∣ ∣ v ∣ ∣ n ||v||_1、||v||_2、||v||_n ∣∣v∣∣1、∣∣v∣∣2、∣∣v∣∣n各自的范数球。以 v = ( x , y ) T v=(x,y)^T v=(x,y)T为例
- ∣ ∣ v ∣ ∣ 1 ≤ C ||v||_1\\leq C ∣∣v∣∣1≤C: ∣ x ∣ + ∣ y ∣ ≤ C |x|+|y|\\leq C ∣x∣+∣y∣≤C
- ∣ ∣ v ∣ ∣ 2 ≤ C ||v||_2\\leq C ∣∣v∣∣2≤C: x 2 + y 2 ≤ C 1 2 x^2+y^2\\leq C_1^2 x2+y2≤C12,也即 x 2 + y 2 ≤ C 2 x^2+y^2\\leq C^2 x2+y2≤C2
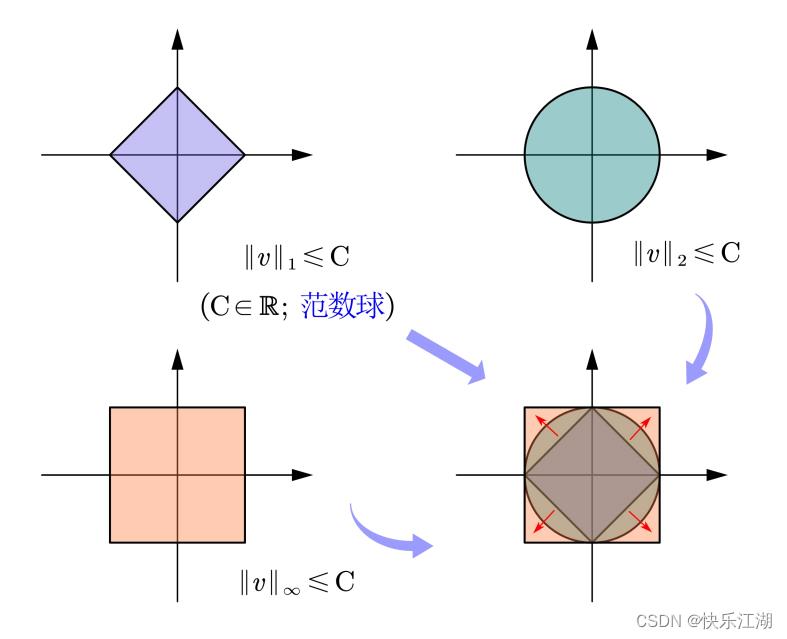
(3)加权的向量范数
加权的向量范数:给定任意的向量范数 ∣ ∣ v ∣ ∣ ||v|| ∣∣v∣∣,可以定义基于矩阵 W ∈ R n × n W\\in \\R^n×n W∈Rn×n的加权范数为
∣ ∣ v ∣ ∣ W = ∣ ∣ W v ∣ ∣ ||v||_W=||Wv|| ∣∣v∣∣W=∣∣Wv∣∣
- 注意:若 W W W为对角矩阵,则 W W W的对角元素分别对应向量各分量的权系数
以 v = ( 1 2 3 ) v=\\beginpmatrix 1\\\\ 2\\\\ 3 \\endpmatrix v=⎝ ⎛1以上是关于最优化所需基础知识-第一节:范数的主要内容,如果未能解决你的问题,请参考以下文章