特定应用程序Rollups
Posted BlockFinance
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了特定应用程序Rollups相关的知识,希望对你有一定的参考价值。

区块链技术正处突破应用的革命边缘。现在越来越多的项目熟悉了模块化和专业化的需求。层出不穷的各类Layer 正在将关注点转移到数据的可用性上,目的是支持更高级别数量级的数据。
同时,计划通过Rollups(Optimistic、ZK 或 Sovereign)扩展计算能力的执行环境和计算层有责任匹配增加的数据能力,并提供足够强大的基础设施以开发实际的应用程序。
计算可扩展性方面带来最大收益的设置可以由以下方式给出:具有交互式争议解决方案的特定类应用程序的Optimistic Rollups。同时,计算可扩展性可以使可编程性和提升改进工具的可能性增加很多。
Cartesi 选择了这条路,为开发人员提供了更方便的开发方式,并有可能使用现实世界操作系统运行现有开源库和组件构建强大的智能合约。
Rollups系统的状态
当我们从软件工程的角度分析它们的代码库时,区块链 DApp 面临的多重技术难题就凸显出来了。像一些经过精心设计的项目 Uniswap ,可以平衡几个相互竞争的目标:对用户的货币价值、极少的 gas 消耗和安全性。不能满足这些标准的应用程序会限制他们的使用群体,使用户处于风险之中,或者在激烈的区块链交互竞争中失败。这种情况不适合应用程序并阻碍创新。
此外,与传统的 Web 2.0 后端服务相比,编码智能合约的用户体验受到了很大的限制。传统 Web 服务器的功能与区块链智能合约之间存在着相当大的的代差是真实的。
以太坊和 EVM Rollups是分散的计算机,它们迫使您应对上述方面。它们是极其缓慢且“特殊的计算机”,需要开发人员使用特定的编程语言进行编码。
在这种奇怪的设置中,开发人员将精力集中在克服这些限制上,而不是优化他们的核心解决方案。结果通常是围绕简单的和有限功能的非必要的、非常复杂的代码。
可扩展性问题:保护特定的应用程序Rollups
每个人都需要验证所有网络,这对于大规模推广采用是不可持续的。在全球共识中,需求量的增加不可避免的导致区块空间提升,进而导致各个应用程序之间恶性竞争。这种情况反而会产生高额费用,对于项目方和用户构成了越来越多的进入成本。为了解决这一难题,以太坊进行了转型,提出了以Rollups为发展中心的路线图。
新的计划中提到可扩展性问题包括两个主要方面:数据可扩展性和计算可扩展性。这两者之间的区别经常被人们忽略,因为他们目前处于相同的gas费用成本中。然而,正是为了通过区分它们,以太坊制定了目前的路线图。
合并后,随着EIP-4844和分片以太坊的发展,将数据添加到其区块链的成本将降低几个数量级。同时,计算扩展已委托给Rollups项目(名称为rollup-centric)。
以太坊协议和Rollups解决方案之间的关系隐藏了一个没有得到重视的问题。与 EVM 兼容的Rollups并不是提升计算可扩展性来匹配以太坊实现数据可用性的最佳设计。
基于 EVM 的Rollups可以描述为计算分片。随着越来越多的应用程序逐渐部署并共享同一个虚拟机,这种设计的缺陷就会出现。争夺虚拟机 CPU 容量的零和游戏将导致问题高端化。每个分片处理上只有一小部分应用程序是可以使用的,其他用户将被逐渐淘汰。这些网络会变得格外拥挤和昂贵。
不过幸运的是,现在可以用不同的方式理解和实用Rollups。可以放弃共享虚拟机,让应用程序拥有自己的 CPU 以及可用的超高性能的计算。资产结算、应用程序之间的可组合性和争议解决可以委托给通用基础层。这种设计称为特定的应用程序Rollups。
特定应用程序Rollups的专用共识与基础层挂钩,允许其验证节点(无论是否允许)保留其结算层的安全保证。换句话说,拥有一个基础层使得 1-of-N 安全模型成为可能,其中任何诚实的验证者都可以在基础层的帮助下,独立于合作执行正确的结果。同时,特定应用程序的共识使应用程序可以享受(非共享)硬件的全部功能。不仅避免了网络高档化的问题,而且还提供了计算可扩展性的显着收益。
从共享共识到特定应用程序共识的转变并不是没有弊端。虽然这种设计意味着应用程序之间的可组合性存在更大的纠葛,但我们认为这对于大多数应用程序来说是一个不太相关的问题。必须等待他们的通信得到验证或依赖软终结技术(即流动性提供者),这并不是一个很大的妥协,以换取应用程序特定链提供的计算能力和可预测性的巨大改进。
特别是具有交互式防欺诈的Optimistic Rollups,为分散式应用程序提供了与主流相当的计算资源(例如,涉及数十亿个指令步骤和大内存地址空间),而无需特殊硬件即可达成共识。这仅仅是可能实现的,因为交互式欺诈证明允许计算资源有限的仲裁者去裁决计算无限的证明者之间的争议。特别是,我们的仲裁者是一个资源有限的结算层,我们的证明者是具有相对无限计算资源的Rollups验证者。为了更好地理解这是如何实现的,请参阅Cartesi Core 技术论文的第 5.2 节。
在寻求最大可扩展性和可定制性的过程中,应用程序和协议开发人员正在将注意力转向不同形式的应用程序特定链。一些例子是:Axie Infinity 的Ronin侧链、dYdX 的主权链、Starkware 的分形缩放设计、Celestia 的模块化执行层。
特定的应用程序Rollups链可以满足这一需求,其优点是不会导致主权(第一层) 特定应用程序链的验证出现危险的碎片化。相反,特定的应用程序Rollups链继承了底层基础层强大的安全性能,而不依赖于已被证明是危险的跨链桥接。
应用程序Rollups链的技术优势源于这样一个事实,即它们对于 N 中 1 的诚实方是安全的,而不是诚实多数的必要性。总而言之,特定应用程序Rollups与特定应用程序的侧链一样好,而不会严重影响安全性。
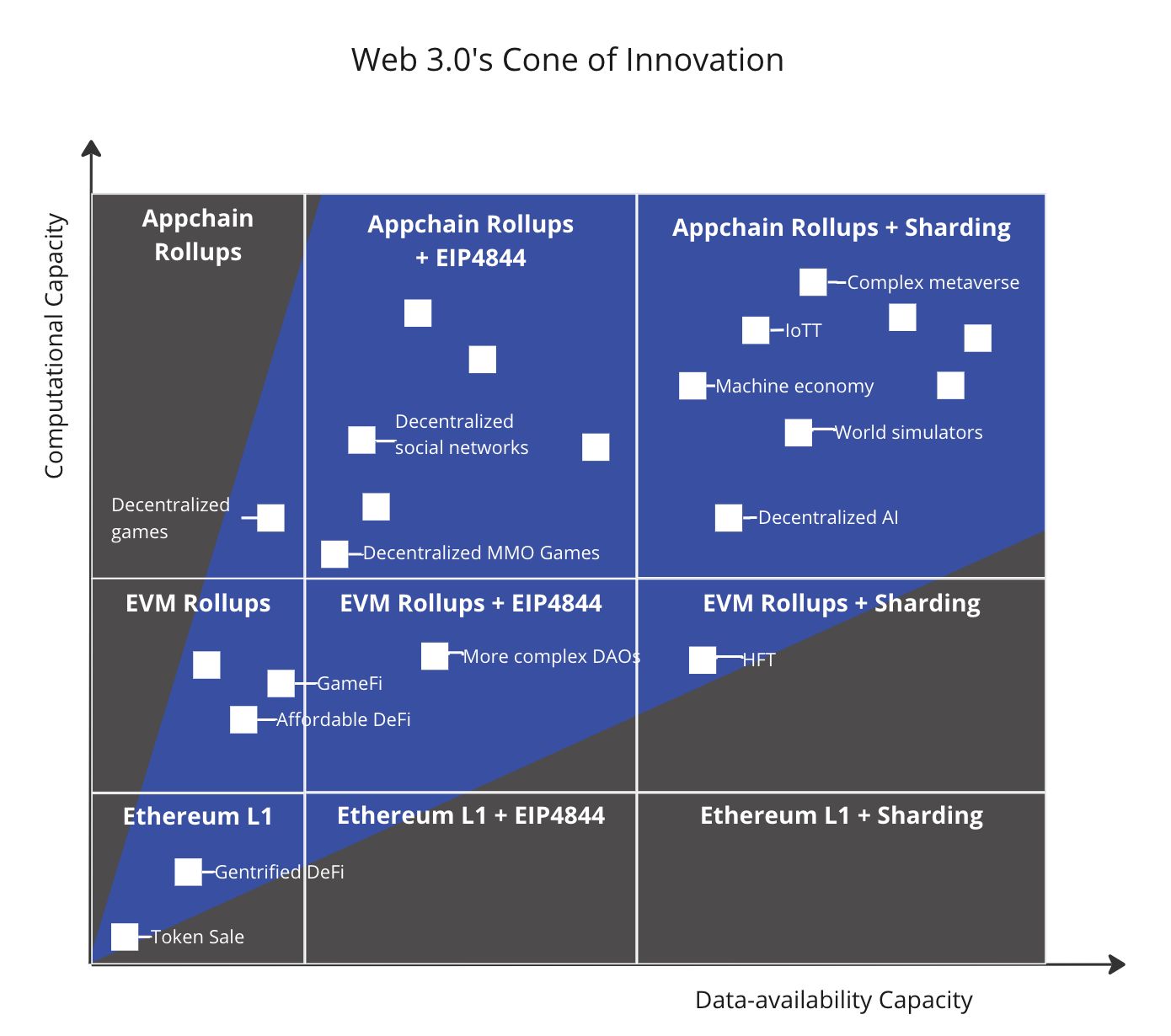
借助上图,可以更好的展示可视化扩展数据和数据可用性容量的效果。
该图分为几个主要区域,表示正在组合的扩展解决方案以及它们在计算和数据容量方面的表现。随着我们从以太坊第一层转移到 EVM Rollups,并最终转移到专用应用链,计算能力得到提高,而数据随着 EIP-4844 和分片的添加也得到了提高。蓝色圆锥显示随着两个维度的缩放,哪些应用逐渐成为可能。我们将蓝色区域称为 web3 的创新锥。
锥体外的灰色区域是不能完全享受数据可用性收益的地方,因为解决方案缺乏计算能力。相反也是这样。白色的小方块是当我们达到这些里程碑时,开始成为可能的应用程序示例,未标记的那些提醒我们,我们不知道一旦环境变得更加健壮,将会出现哪些酷炫的新应用程序。
创新椎不能完全代表精确的数据。所画出的方向和角度不能按字面意思理解。而且,每个地区有可能的应用程序很容易进入不同的领域。该图只是对分散应用程序不断增长的创新视野中提供了一个直观的展望。
可编程性问题:为更好的抽象辩护
除了上述计算限制之外,DApps 的开发人员还面临着另一个巨大的负担:缺乏成熟的环境,表现出来就是软件工具和库的不足。
为了更好地说明这个问题,让我们提一下最近几天我们遇到的最令人印象深刻的去中心化游戏Topology。这个雄心勃勃的项目将战略基础设施建设和行星动力学相结合!疯狂的事情。然而,仅仅通过查看他们的源代码,我们就看到了他们必须杀死的野兽。举一个例子,他们必须开发一种从头开始模拟行星动力学的经典算法。在 Topology 团队所展现的令人印象深刻的人才背后,有一个令人担忧的问题:只有优秀的开发人员才能在如此不成熟的环境中将他们的想法变为现实。
上面的例子并不是单独存在的。如此多的库(例如:1、2、3、4、5、6、7 )是用Solidity编写的,以帮助开发智能合约和 DApp 。但是目前语言的状态还很不成熟,一些基本的任务还需要人们求助于论坛,寻求帮助。
这不是传统软件行业的现实。例如,游戏愤怒的小鸟需要与拓扑相同的库(毕竟,行星和飞鸟遵循相同的物理定律)。然而,愤怒的小鸟背后的开发人员并没有被迫从头开始编写他们需要的每一行代码。基本上每种可以想象的语言有成熟的库。
为了使传统开发人员能够访问所有这些库,这也是解决可编程性问题的黄金标准,需要成熟的操作系统。从 Web2 到传统游戏,再到卫星发射,各个领域的开发人员都依靠操作系统为他们提供所需的支持。他们实现想法所需的语言和库使他们能够将精力集中在他们真正想要构建的东西上,而不是使之成为可能的底层基础设施。
这就是我们选择 RISC-V 架构来构建Rollups解决方案的原因。它可以将Linux或其他操作系统移植到Rollups中。这样,开发人员可以用他们最熟悉的语言和库,并且将他们的想法变为现实,而不会放弃区块链的可靠安全保证,如之前的文章(1、2、3 )所述。
到目前为止,Linux 一直是重点,它是一个可以运行任何可以编译为 RISC-V 的操作系统,例如一些非常安全的微内核。
Cartesi Rollups
我们首先讨论了模块化汇总执行层的重要性,该层真正扩展了计算并防止 DApp 在计算资源的零和游戏中相互参与。然后我们详细阐述了开发人员像主流开发人员一样依靠操作系统的抽象能力的重要性。
正是考虑到这两个需求,我们将Cartesi Rollups设计和构建为模块化执行层,为 DApp 提供以下扩展优势:
- 每个 DApp 都有自己的高性能汇总应用链和专用 CPU;
- Cartesi 生态系统中其他 DApp 的资源不会被蚕食;
- 零和游戏环境之外的计算可扩展性显着提高;
- 保留底层区块链的强大安全保障;
- 一个成熟的操作系统,为开发人员提供工业级工具。
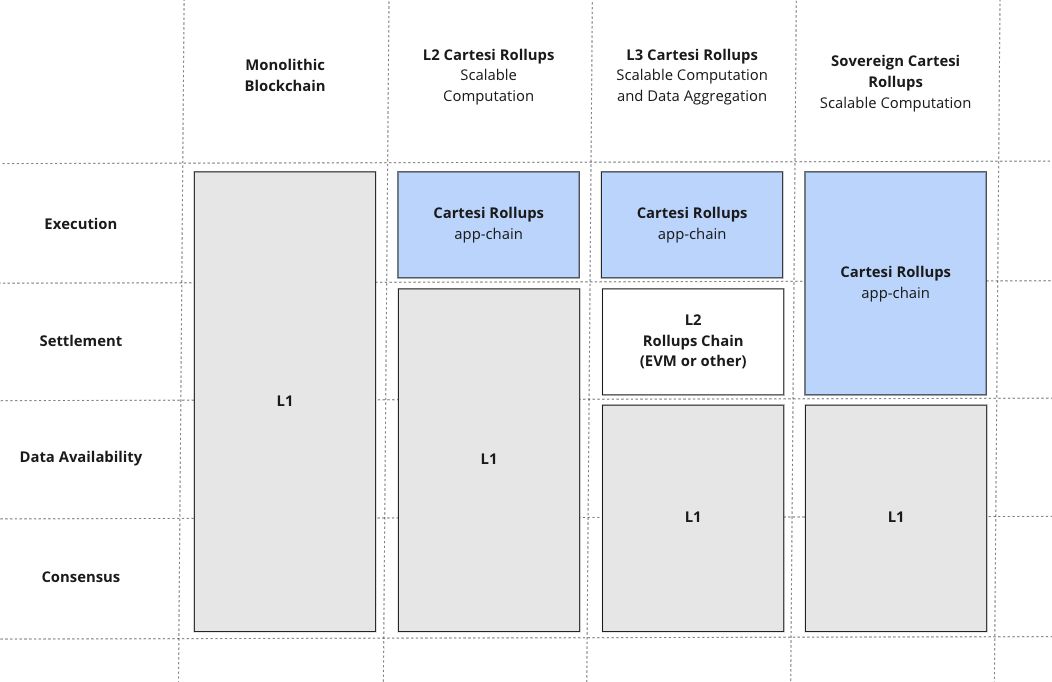
Cartesi Rollups 应用程序可以用作第二层(即在以太坊之上)、第三层(即在 Arbitrum 或 ZK-EVM 链之上)或作为主权Rollups(即在 Celestia 之上)。开发人员可以通过最少的代码更改将他们的应用程序从一个平台移植到另一个平台。
最后的话
Cartesi 允许开发人员专注于他们正在构建的内容,而不会使他们在构建过程中或他们需要处理问题时遇到不便的限制。
这样,创新就可以在流行的应用程序不蚕食不太成熟的应用程序的情况下推动创新。 去中心化的应用程序可以拥有他们需要的所有计算能力,同时保持成本的可预测性。 开发人员可以利用经过实战考验的编程库并创建去中心化的 MMORPG,这些游戏实际上很有趣。
从可定制性的角度来看,Cartesi Rollups 应用链为 DApp 提供了为不同操作收取不同价格的可能性。 例如,他们可以在去中心化交易所免除做市商的gas费,或者增加海洋模拟器 DApp 上掠夺性捕鱼的成本。
Cartesi 对去中心化技术即将发生的革命有着非常清晰的愿景。 Cartesi Rollups 正在开发中,作为对这种新环境需求的聚焦解决方案。
关于Cartesi
区块链操作系统正在构建 Cartesi Rollups,这是一个模块化执行层,可将简单的智能合约提升到去中心化的 Linux操作系统中运行。它允许开发人员启动高度可扩展的Rollups链,并使用他们最喜欢的语言和软件组件编写去中心化逻辑。
- 每个 DApp 都有自己的高性能Rollups链;
- Cartesi 生态系统中其他 DApp 的资源不会被蚕食;
- 没有提高网络门槛;
- 可以启用目前无法在 EVM 链上运行的全新类别的 DApp;
- 保留底层区块链的强大安全保障
欢迎来到区块链操作系统,可以了解下一步计划。

BSV 上的 ZK-Rollups
ZK-Rollups 被认为是以太坊 Layer 2 扩容解决方案的圣杯。
总的来说,我个人的看法是,在短期内,Optimistic-Rollups 可能会在通用 EVM 计算中胜出,而 ZK-Rollups 可能会在简单支付,交换和其他特定于应用程序的用例中胜出,但从中长期来看,随着 ZK-SNARK 技术的改进,ZK-Rollups 将在所有用例中胜出。 — Vitalik
我们已经直接在 BSV 上实现了第一个 ZK-Rollups (ZKR)。此外,我们展示了为什么 ZKR 在 BSV 上比在以太坊上效果更好。
ZK-Rollups 如何在以太坊中运作
ZKR 的核心是利用 ZK-SNARK 证明的简洁性:验证某些计算是否正确完成比重新执行它更有效。不是处理链上的每笔交易,而是首先将合约的多个交易发送给协调器(又名定序器/中继器),而不是矿工。协调器将它们“滚动”捆绑到单个事务中。该交易包含一个简洁的证明,证明所有这些批量交易都被忠实处理,将合约状态从 state1 更改为 state2,并发送给矿工。
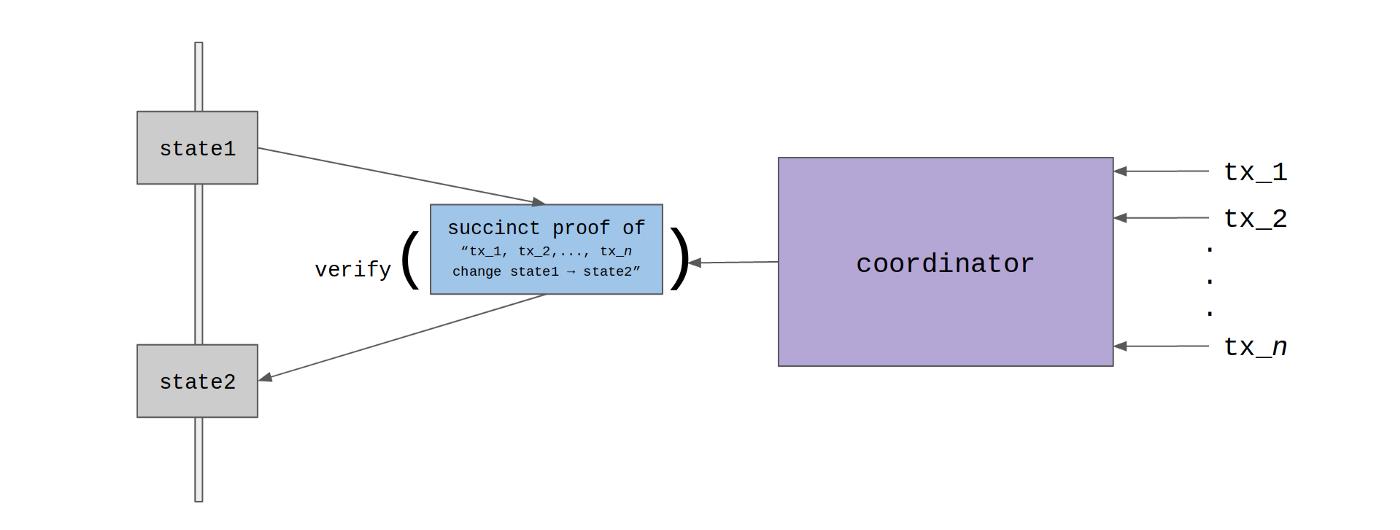
由于交易处理的所有繁重工作都外包给了链外,因此区块链可以在给定的时间间隔内处理更多的交易,从而扩大规模。zkSNARK 证明确保了链下状态转换的正确性,使协调者无法提交无效的状态转换。这使得 ZKR 成为吸引人的 L2 可扩展性解决方案,因为它允许在不牺牲 L1 安全性的情况下进行扩展,这与 Plasma 和 Optimistic Rollup 等许多其他 L2 解决方案不同。
ZK-Rollups 代币
我们以代币为例来演示如何使用 ZKR。
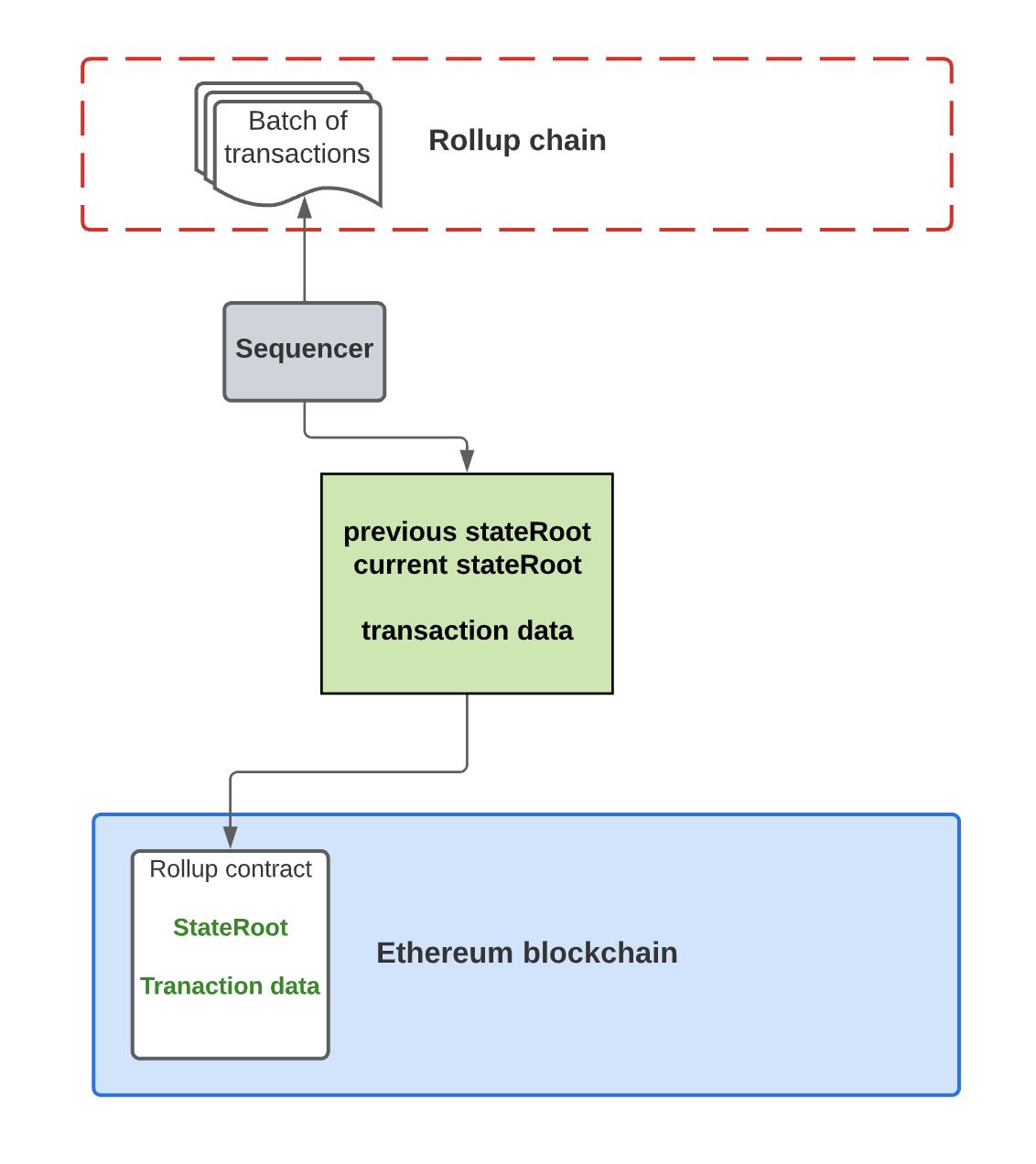
主链上有一个 Rollup 合约,跟踪根状态。“根状态”是默克尔树的根。树的每一片叶子都是一个帐户,由其所有者的公钥或地址及其属性(例如余额)组成。

在以下示例中,将两笔存款被打包为一个交易。

BSV 上的 Rollup
我们已经在 BSV 上实现了 Rollup 合约。它确保在处理完一批事务后,当前根状态被正确地更新。
import "zksnark.scrypt";
// a simple zk Rollup for token transfers
contract ZKRollup
const VerifyingKey vk;
@state
int acount_root;
public function verify(int new_account_root, Proof proof, SigHashPreimage txPreimage)
int[ZKSNARK.N] inputs = [this.account_root, new_account_root];
// verify proof
require(ZKSNARK.verify(inputs, proof, this.vk));
// update root
this.account_root = new_account_root;
require(this.propagateState(txPreimage, SigHash.value(txPreimage)));
它跟踪的唯一状态是第 8 行中帐户树的根。有效性证明在第 14 行使用我们之前的 zk-SNARK 库进行验证。Root 在第 17 行更新。第 5 行的验证密钥来自 zk-SNARK 的设置阶段。
生成 ZKR 证明
我们需要以 zk-SNARK 友好的方式对我们的事务处理逻辑进行编码。
一种流行的语言是 Circom。由于篇幅所限,我们不在这里介绍 Circom 语法,而是请读者参考 circom 官方网站了解更多信息。
处理单个事务涉及:
- 通过默克尔证明检查发件人帐户是否在树中
- 验证发件人的签名
- 更新发送者的余额并验证中间默克尔根
- 更新接收方的余额
- 更新默克尔树的根
我们可以像这样重用现有的 Rollup Circom 代码。
template ProcessTx(k)
// k is depth of accounts tree
// accounts tree info
signal input accounts_root;
signal private input intermediate_root;
signal private input accounts_pubkeys[2**k, 2];
signal private input accounts_balances[2**k];
// transactions info
signal private input sender_pubkey[2];
signal private input sender_balance;
signal private input receiver_pubkey[2];
signal private input receiver_balance;
signal private input amount;
signal private input signature_R8x;
signal private input signature_R8y;
signal private input signature_S;
signal private input sender_proof[k];
signal private input sender_proof_pos[k];
signal private input receiver_proof[k];
signal private input receiver_proof_pos[k];
// output
signal output new_accounts_root;
// 1. verify sender account exists in accounts_root
component senderExistence = LeafExistence(k, 3);
senderExistence.preimage[0] <== sender_pubkey[0];
senderExistence.preimage[1] <== sender_pubkey[1];
senderExistence.preimage[2] <== sender_balance;
senderExistence.root <== accounts_root;
for (var i = 0; i < k; i++)
senderExistence.paths2_root_pos[i] <== sender_proof_pos[i];
senderExistence.paths2_root[i] <== sender_proof[i];
// 2. check that transaction was signed by sender
component signatureCheck = VerifyEdDSAMiMC(5);
signatureCheck.from_x <== sender_pubkey[0];
signatureCheck.from_y <== sender_pubkey[1];
signatureCheck.R8x <== signature_R8x;
signatureCheck.R8y <== signature_R8y;
signatureCheck.S <== signature_S;
signatureCheck.preimage[0] <== sender_pubkey[0];
signatureCheck.preimage[1] <== sender_pubkey[1];
signatureCheck.preimage[2] <== receiver_pubkey[0];
signatureCheck.preimage[3] <== receiver_pubkey[1];
signatureCheck.preimage[4] <== amount;
// 3. debit sender account and hash new sender leaf
component newSenderLeaf = MultiMiMC7(3,91)
newSenderLeaf.in[0] <== sender_pubkey[0];
newSenderLeaf.in[1] <== sender_pubkey[1];
newSenderLeaf.in[2] <== sender_balance - amount;
// update accounts_root
component computed_intermediate_root = GetMerkleRoot(k);
computed_intermediate_root.leaf <== newSenderLeaf.out;
for (var i = 0; i < k; i++)
computed_intermediate_root.paths2_root_pos[i] <== sender_proof_pos[i];
computed_intermediate_root.paths2_root[i] <== sender_proof[i];
// check that computed_intermediate_root.out === intermediate_root
computed_intermediate_root.out === intermediate_root;
// 4. verify receiver account exists in intermediate_root
component receiverExistence = LeafExistence(k, 3);
receiverExistence.preimage[0] <== receiver_pubkey[0];
receiverExistence.preimage[1] <== receiver_pubkey[1];
receiverExistence.preimage[2] <== receiver_balance;
receiverExistence.root <== intermediate_root;
for (var i = 0; i < k; i++)
receiverExistence.paths2_root_pos[i] <== receiver_proof_pos[i];
receiverExistence.paths2_root[i] <== receiver_proof[i];
// credit receiver account and hash new receiver leaf
component newReceiverLeaf = MultiMiMC7(3,91)
newReceiverLeaf.in[0] <== receiver_pubkey[0];
newReceiverLeaf.in[1] <== receiver_pubkey[1];
newReceiverLeaf.in[2] <== receiver_balance + amount;
// 5. update accounts_root
component computed_final_root = GetMerkleRoot(k);
computed_final_root.leaf <== newReceiverLeaf.out;
for (var i = 0; i < k; i++)
computed_final_root.paths2_root_pos[i] <== receiver_proof_pos[i];
computed_final_root.paths2_root[i] <== receiver_proof[i];
// output final accounts_root
new_accounts_root <== computed_final_root.out;
这里是对上述代码的详细解释。
多笔交易
只有当多个事务一起批处理时,rollup的优点才会显现出来。仅当批次中的所有交易都有效时,生成的证明才有效。
for (var i = 0; i < 2**m - 1; i++)
// transactions existence and signature check
txExistence[i] = TxExistence(m);
txExistence[i].from_x <== from_x[i];
txExistence[i].from_y <== from_y[i];
txExistence[i].to_x <== to_x[i];
txExistence[i].to_y <== to_y[i];
txExistence[i].amount <== amount[i];
txExistence[i].token_type_from <== token_type_from[i];
txExistence[i].tx_root <== tx_root;
...
总结
ZKR 将交易数据存储在第 1 层(L1)的链上,以实现数据可用性。底层 L1 的存储成本为 ZKR 的可扩展性增益设置了上限。因此,ZKR 在 BSV 上的效果比在以太坊上要好得多,因为前者的存储成本比后者便宜几个数量级。
此外,由于 zk-SNARK 是通用的,一旦在 BSV 上部署了 rollup 智能合约,许多现有的在其他区块链(如 Circom 和 ZoKrates)上设计的 ZKR 工具可以直接在 BSV 中重复使用。这意味着 ZKR 可用于今天在 BSV 上扩展应用程序。
参考
[1] https://blog.matter-labs.io/optimistic-vs-zk-rollup-deep-dive-ea141e71e075
[2] https://www.preethikasireddy.com/post/a-normies-guide-to-rollups
[3] https://github.com/barryWhiteHat/roll_up_token
[4] https://blog.matter-labs.io/optimistic-vs-zk-rollup-deep-dive-ea141e71e075
以上是关于特定应用程序Rollups的主要内容,如果未能解决你的问题,请参考以下文章