基于模糊PID的混合磁悬浮减振器的设计及控制研究

Posted 2022-10-12 fpga和matlab

目录

一、理论基础

二、核心程序

三、仿真测试结果

---

作者ID  ：fpga和matlab
CSDN主页：https://blog.csdn.net/ccsss22?type=blog
擅长技术：
1.无线基带,无线图传,编解码 
2.机器视觉,图像处理,三维重建 
3.人工智能,深度学习 
4.智能控制,智能优化
5.其他

一、理论基础

        磁流变减振控制的阻尼具有可控性、非线性、滞后和饱和等特性,控制器的开发具有非常大的复杂性.结合磁流变阻尼控制器的控制原理以及设计功能进行模糊PID控制,提出采用三闭环磁流变阻尼控制系统的设计思路.包括加速度环、电压环和电流环,以保证控制系统的精度和实时性,本文详细介绍并进行了磁流变减振控制器的硬件电路设计和DSP控制系统的软件设计,对磁流变减振控制的台架试验.试验结果表明,磁流变阻尼控制器是准确可行的.

       采用模糊自适应PID控制器的车辆行驶控制仿真设计，旨在解决前车自动跟车，接收前车传输的行驶状态，计算前方路况，实现自动驾驶控制的实现。主要设计过程是基于预览理论设计汽车的自动跟随模型并指定要跟随的物理量。模糊PID控制器设计控制方法跟踪给定的物理量，仿真结果为获得。该方法已被证明具有良好的鲁棒性，可确保智能汽车具有良好的路况计算和车辆跟踪精度。并且模糊PID人智能控制器比传统的PID控制器更健壮，控制精度更高。

这是减振系统的原理图

这是减振系统的电磁模块

电磁模块不太理解的话 我有参考文献供参考。

要求设计LQR控制器通过matlab作出 在外力干扰下

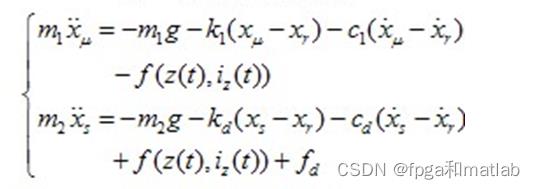
其中Xs，Xr，Xu本质上均为t的关系式。

这里，我们需要做一个假设，即Xr的二阶导数为0。（否则三个变量，两个方程，没法求解的）

这样，我们就可以建立关于地面位移的相对位移的方程式

于是上面的式子可以等效为：

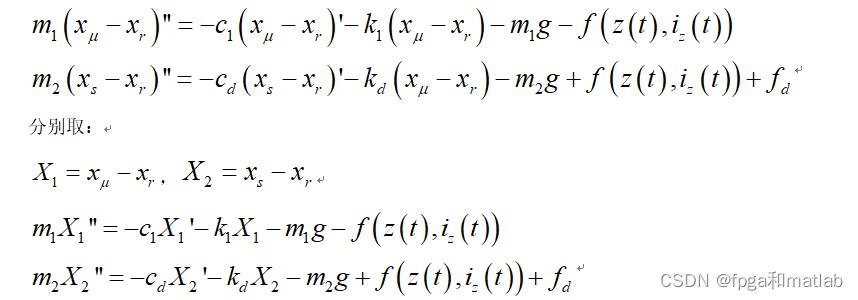
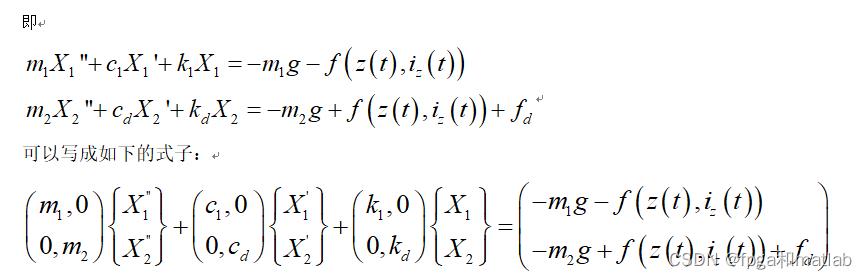 因此，这个系统满足振动系统的基本方程模式。

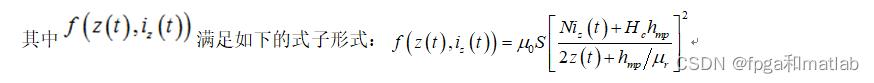
我们根据上面的模型，进行控制对象的建模，然后再基于这个控制对象，进行LQR控制器的设计，最后在Simulink中仿真实现。

        这个式子和一般式子不同的是，他的方程右边有一个随着时间而发生变化的变量。

这个方程，我们用如下的式子表示：

 假设系统的控制输出Z，那么Z的表达式为：

 

以上就是推导得到的系统的状态方程，下面我们基于这个状态方程计算对应的LQR控制器。

       根据上面的式子，我们可以设计最优LQR控制器：

下面，我们讨论一下关于输入U1和U2，从方程上讲，U1和U2，就是对应的

 

这里，随时间变化的就是f这个变量，mg和fd为常量。 

二、核心程序

clc;
clear;
close all;
warning off;

m1  = 25;
m2  = 20;
S   = 0.009;
N   = 500;
R   = 1;
i0  = 0.2;
lnm = 64;
A   = 5.12;
k1  = 0.3;
kd  = 0.6;
c1  = 0.5;
cd  = 0.3;

g   = 9.18;
L0  = 1000;
k1s = -244043.62;
k2s = -5002.34;
k3s = -35.68;
m   = 311.84;
z0  = 20;
u0  = 10;
Hc  = 800;
hmp = 34;
ur  = 10000;


%计算状态方程
AA1 = [0,0,m1,0;
       0,0,0,m2;   
       m1,0,0,0;
       0,m2,0,0;];
AA2= [-m1,0,0,0;
      0,-m2,0,0;
      0,0,k1,0;
      0,0,0,kd];
AA = -inv(AA1)*AA2;


BB1= AA1;
BB2= [0,0;
      0,0;
      1,0;
      0,1];
BB = inv(BB1)*BB2;


CC = [1,0,0,0;
      0,1,0,0;
      0,0,0,0;
      0,0,0,0];
  
DD = [0,0;
      0,0;
      0,0;
      0,0];  
  
sys=ss(AA,BB,CC,DD)  
  
Q               = diag([5 1 2 6]);
R               = eye(2);
k               = LQR(AA,BB,Q,R);


%The LQR Controller
k11             = k(1,1);
k21             = k(1,2);
k31             = k(1,3);
k41             = k(1,4);


k12             = k(2,1);
k22             = k(2,2);
k32             = k(2,3);
k42             = k(2,4);

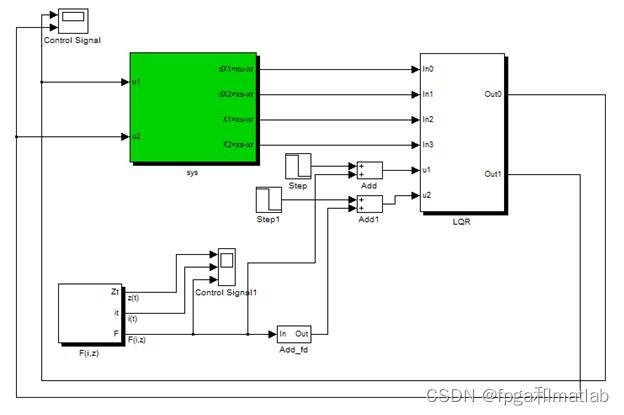
三、仿真测试结果

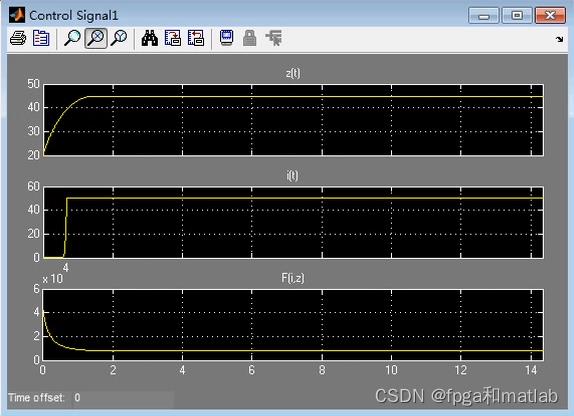
 A08-29