深度时空残差网络在城市人流量预测中的应用

Posted 2022-10-01 AI浩

文章目录

• 摘要
• 简介
• 预备知识
• 人流量问题的制定
• • 深度残差学习
  • 深度时空残差网络
  • 前三个成分的结构
  • 外部组件的结构
• 融合
• 算法和优化
• 实验
• • 设置
  • 结果TaxiBJ
  • 结果BikeNYC
• 相关工作
• 总结及未来工作

摘要

  人群流量预测对交通管理和公共安全具有重要意义，同时也受到跨区域交通、事件、天气等复杂因素的影响，具有很大的挑战性。我们提出了一种基于深度学习的方法，称为ST-ResNet，用来集体预测城市每个区域的人群流入和流出。基于时空数据的独特属性，设计了一种端到端的ST-ResNet结构。更具体地说，我们使用残差神经网络框架来建模人群交通的时间距离、周期和趋势属性。针对每个特性，我们设计了残差卷积单元的分支，每个分支都模拟了人群交通的空间特性。ST-ResNet学会基于数据动态聚合三个残差神经网络的输出，给不同的分支和区域分配不同的权重。聚合进一步结合外部因素，如天气和星期几，预测每个地区的人群最终流量。对北京和纽约两种类型的人群流动的实验表明，提出的ST-ResNet优于6种已知的方法。

简介

  预测城市的人流量对交通管理和公共安全具有重要意义(Zheng et al. 2014)。例如，在2015年的上海跨年庆典上，大量人群涌入一个狭长地带，导致了灾难性的踩踏事件，造成36人死亡。2016年7月中旬，数百名“精灵宝可梦Go”玩家跑过纽约中央公园，希望抓住一个特别罕见的数字怪物，导致那里发生了危险的踩踏事件。如果可以预测一个地区的人流量，就可以通过使用紧急机制，如实施交通管制、发出警告或提前疏散人员，来减轻或防止这种悲剧。

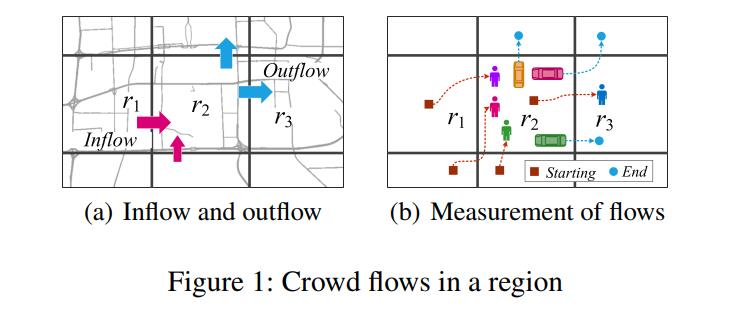
  本文预测了两种人群流动类型(Zhang et al. 2016):流入和流出，如图1(a)所示。流入是指在一定时间间隔内从其他地方进入一个地区的人群的总流量。外流指的是在一定时间间隔内离开一个地区前往其他地方的人群的总交通流量。这两种流动都追踪人群在地区之间的转移。了解它们对风险评估和交通管理非常有益。资金流入/流出

  可以通过行人数量、附近道路上行驶的汽车数量、乘坐公共交通系统(如地铁、公共汽车)的人数来衡量，如果有数据的话，可以将所有这些综合起来衡量。图1(b)给出了一个例子。我们可以用手机信号来测量行人的数量，可见r2的流入和流出分别为(3;1)分别。同理，利用车辆的GPS轨迹，两种流类型分别为(0;3)。

预备知识

在本节中，我们将简要回顾人流量预测问题(Zhang et al. 2016;Hoang, Zheng, and Singh 2016)，并介绍了深度剩余学习(He et al. 2016)。

人流量问题的制定

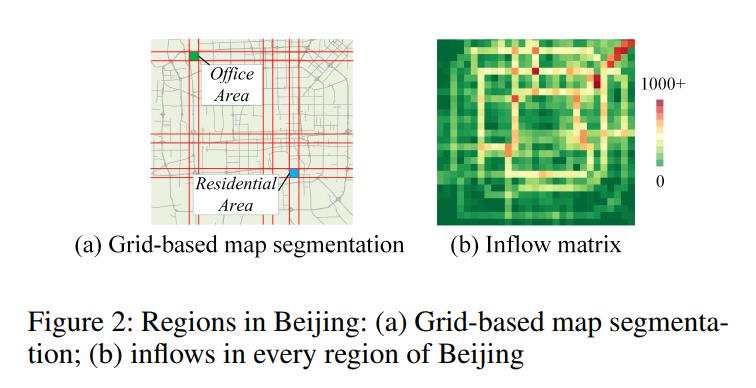
定义1 (Region (Zhang et al. 2016))根据不同的粒度和语义，位置有很多定义。在本研究中，我们根据经纬度将一个城市划分为I \\times J网格地图，其中网格表示一个区域，如图2(a)所示。

定义2(流入/流出(Zhang et al. 2016))设$\mathbb{P}$是$t^{\text{th}}$时间间隔上的轨迹集合。对于位于第$i^{\text{th}}$行和第$j^{\text{th}}$列的网格(i, j)，在时间间隔$t$处人群的流入和流出分别定义为

$$\begin{array}{rl}{x}_t^{in,i,j}& =\sum _{Tr\in \mathbb{P}}\left|k>1\mid g_{k-1}\notin (i,j)\wedge g_k\in (i,j)\right|\\ x_t^{\text{out },i,j}& =\sum _{Tr\in \mathbb{P}}\left|k\ge 1\mid g_k\in (i,j)\wedge g_{k+1}\notin (i,j)\right|\end{array}$$

其中$\mathrm{Tr}$: $g_1\to g_2\to \cdots \to g_{|Tr|}$是$\mathbb{P}$中的轨迹，$g_k$是地理空间坐标;$G_k\in (i,j)$表示点$G_k$位于网格(i, j)内，反之亦然;$|\cdot |$表示集合的基数。

在$t^{\text{th}}$时间区间，所有I \\times J区域的流入和流出可以表示为一个张量${\mathbf{X}}_{t}in{\mathbb{R}}^{2\times I\times J}where{\left({\mathbf{X}}_t\right)}_{0,I,J}=x_t^{In,I,J}，{\left({\mathbf{X}}_t\right)}_{1,I,J}=x_t^{\text{out}，I,J}$。流入矩阵如图2(b)所示。

形式上，对于一个由$I\times J$网格图表示的空间区域上的动力系统，随着时间的推移，每个网格中有两种类型的流动。因此，任何时刻的观测可以用一个张量$\mathbf{X}\in {\mathbb{R}}^{2\times I\times J}$表示。

问题1给定历史观察${\mathbf{X}}_t\mid t=0，\cdots ,n-1$，预测${\mathbf{X}}_n$

深度残差学习

深度残差学习(He et al. 2015)允许卷积神经网络具有100层甚至超过1000层的超深结构。该方法已经在多个具有挑战性的识别任务中显示了先进的结果，包括图像分类、目标检测、分割和定位(He et al. 2015)。

形式上，具有标识映射的残差单元(He et al. 2016)定义为:

$${\mathbf{X}}^{(l+1)}={\mathbf{X}}^{(l)}+\mathcal{F}\left({\mathbf{X}}^{(l)}\right)$$

其中${\mathbf{X}}^{(l)}和{\mathbf{X}}^{(l+1)}$分别为$l^{th}$残差单元的输入和输出;\\mathcalF是残差函数，例如，两个$3\times 3$卷积层的堆栈(He et al. 2015)。残差学习的核心思想是学习关于${\mathbf{X}}^{(l)}$的加性残差函数$\mathcal{F}$ (He et al. 2016)。

深度时空残差网络

图3展示了ST-ResNet的体系结构，它由四个主要组件组成，分别建模时间紧密度、周期、趋势和外部影响。如图3的右上部分所示，我们首先使用定义1和定义2中介绍的方法，将流经城市的每个时间间隔的流入和流出分别转化为两个通道的类图像矩阵。然后我们将时间轴分成三个片段，分别表示最近的时间、近历史和遥远的历史。然后将每个时间片段中区间的2通道流矩阵分别输入前三个组件，分别对上述三个时间属性进行建模:接近度、周期和趋势。前三个组成部分与卷积神经网络共享相同的网络结构，然后是残差单元序列。这种结构体现了远近区域之间的空间依赖性。在外部组件中，我们从外部数据集中手动提取一些特征，如天气条件和事件，将它们输入到一个两层完全连接的神经网络中。将前三个分量的输出融合为基于参数矩阵的$X_{Res}$，对不同区域不同分量的结果赋予不同的权重。$X_{Res}$与外部组件$X_{Ext}$的输出进一步集成。最后，聚合映射到[−1;1]，它在反向传播学习过程中产生比标