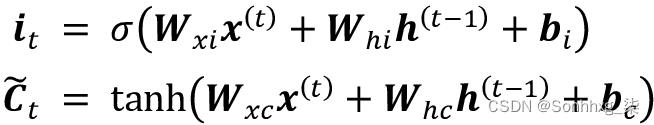NLP使用递归神经网络对序列数据进行建模 （Pytorch）

Posted 2022-09-26 Sonhhxg_柒

  🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​

📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

在上一章中，我们专注于卷积神经网络( CNN )。我们介绍了 CNN 架构的构建块以及如何在 PyTorch 中实现深度 CNN。最后，您学习了如何使用 CNN 进行图像分类。在本章中，我们将探索循环神经网络( RNN ) 并了解它们在序列数据建模中的应用。

我们将涵盖以下主题：

• 引入顺序数据
• 用于建模序列的 RNN
• 长短期记忆
• 随时间截断的反向传播
• 在 PyTorch 中实现用于序列建模的多层 RNN
• 项目一：IMDb影评数据集的RNN情感分析
• 项目二：使用来自儒勒·凡尔纳的《神秘岛》的文本数据，使用 LSTM 单元进行 RNN 字符级语言建模
• 使用渐变剪裁来避免爆炸渐变

引入顺序数据

让我们通过查看 RNN 的性质来开始我们对 RNN 的讨论序列数据，通常称为序列数据或序列。我们将研究使它们与其他类型的数据不同的序列的独特属性。然后，我们将了解如何表示序列数据并探索基于模型输入和输出的序列数据模型的各种类别。这将有助于我们在本章中探索 RNN 和序列之间的关系。

建模顺序数据——顺序很重要

是什么使得与其他类型的数据相比，序列的独特之处在于序列中的元素以一定的顺序出现，并且彼此之间并不独立。用于监督学习的典型机器学习算法假设输入是独立同分布（IID）数据，这意味着训练样本是相互独立的，并且具有相同的底层分布。在这方面，基于相互独立的假设，将训练样例提供给模型的顺序是无关紧要的。例如，如果我们有一个包含n 个训练示例的样本，则x (1) , x (2) , ..., x ( n )，我们使用数据来训练我们的机器学习算法的顺序并不重要。这种情况的一个例子是我们之前使用的 Iris 数据集。在 Iris 数据集中，每朵花都是独立测量的，一朵花的测量值不会影响另一朵花的测量值。

然而，当我们处理序列时，这个假设是无效的——根据定义，顺序很重要。预测特定股票的市场价值就是这种情况的一个例子。例如，假设我们有一个包含n 个训练样例的样本，其中每个训练样例代表某只股票在特定日期的市场价值。如果我们的任务是预测未来三天的股票市场价值，那么按照日期排序的顺序考虑以前的股票价格来推导趋势而不是按随机顺序使用这些训练示例是有意义的。

序列数据与时间序列数据

时间序列数据是特殊类型的顺序数据，其中每个示例都与时间维度相关联。在时间序列数据中，样本是在连续的时间戳上进行的，因此，时间维度决定了数据点之间的顺序。例如，股票价格和语音或语音记录是时间序列数据。

另一方面，并​​非所有的顺序数据有时间维度。为了例如，在文本数据或 DNA 序列中，示例是有序的，但文本或 DNA 不符合时间序列数据的条件。正如您将看到的，在本章中，我们将重点介绍非时间序列数据的自然语言处理 (NLP) 和文本建模示例。但是请注意，RNN 也可以用于时间序列数据，这超出了本书的范围。

表示序列

我们已经建立了这个顺序数据点之间的排序在顺序数据中很重要，因此我们接下来需要找到一种在机器学习模型中利用这种排序信息的方法。在本章中，我们将序列表示为

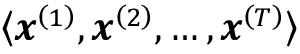
。上标索引表示实例的顺序，序列的长度为T。对于一个合理的序列示例，请考虑时间序列数据，其中每个示例点x ( t )属于特定时间t。图 15.1显示了一个时间序列数据示例，其中输入特征 ( x ) 和目标标签 ( y ) 自然地按照时间轴的顺序排列；因此，两个x's 和y是序列。

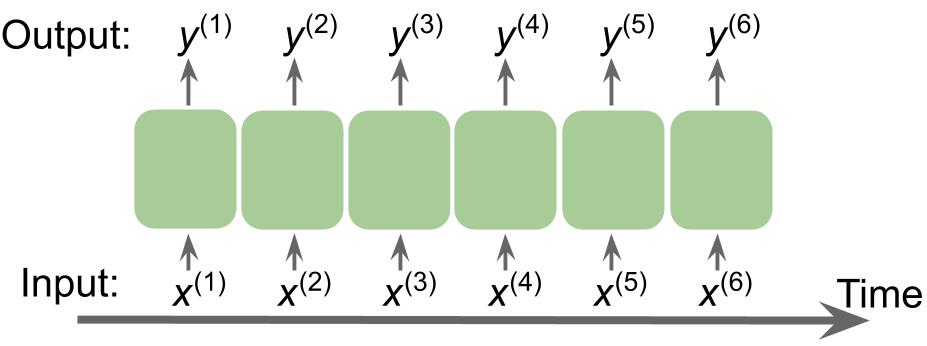
图 15.1：时间序列数据示例

正如我们已经提到的，到目前为止，我们已经介绍了标准的 NN 模型，例如多层感知器( MLP ) 和用于图像数据的 CNN 假设训练示例彼此独立，因此不包含排序信息。我们可以说这样的模型没有以前见过的训练例子的记忆。例如，样本通过前馈和反向传播步骤，权重的更新与训练样本的处理顺序无关。

相比之下，RNN 是为序列建模而设计的，能够记住过去的信息并相应地处理新事件，这在处理序列数据时是一个明显的优势。

不同类别的序列建模

序列建模有许多引人入胜的应用，例如语言翻译（例如，将文本从英语翻译成德语）、图像字幕和文本生成。然而，为了选择合适的架构和方法，我们必须理解并能够区分这些不同的序列建模任务。图 15.2基于Andrej Karpathy 2015 年 ( The Unreasonable Effectiveness of Recurrent Neural Networks ) 的优秀文章The Unreasonable Effectiveness of Recurrent Neural Networks中的解释，总结了最常见的序列建模任务，依赖于输入和输出数据的关系类别。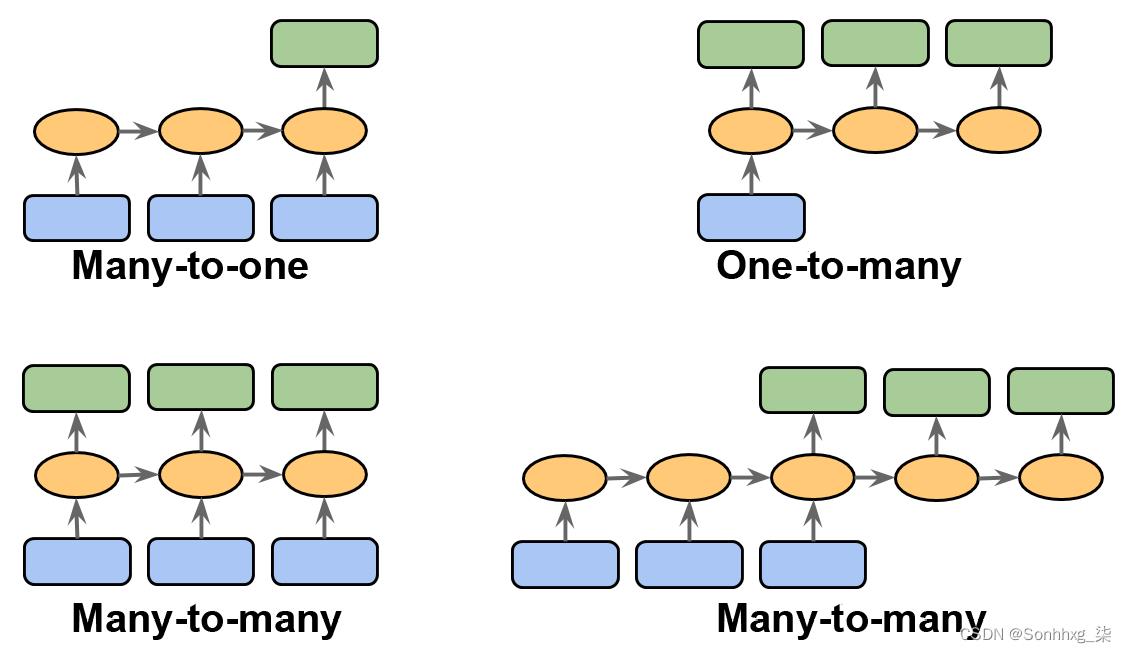

图 15.2：最常见的排序任务

让我们更详细地讨论上图中描述的输入和输出数据之间的不同关系类别。如果输入和输出数据都不代表序列，那么我们处理的是标准数据，我们可以简单地使用多层感知器（或本书前面介绍的其他分类模型）对此类数据进行建模。但是，如果输入或输出是一个序列，则建模任务可能属于以下类别之一：

• 多对一：输入数据是一个序列，但输出是一个固定大小的向量或标量，而不是一个序列。例如，在情感分析中，输入是基于文本的（例如，电影评论），输出是类标签（例如，表示评论者是否喜欢电影的标签）。
• 一对多：输入数据是标准格式而不是序列，但输出是序列。此类别的一个示例是图像字幕——输入是图像，输出是总结该图像内容的英文短语。
• 多对多：两者输入和输出数组是序列。这个类别可以根据输入和输出是否同步来进一步划分。同步多对多建模任务的一个示例是视频分类，其中视频中的每一帧都被标记。延迟多对多建模任务的一个示例是将一种语言翻译成另一种语言。例如，在翻译成德语之前，必须由机器阅读和处理整个英语句子。

现在，在总结了序列建模的三大类之后，我们可以继续讨论 RNN 的结构。

用于建模序列的 RNN

在本节中，在我们开始之前在 PyTorch 中实现 RNN，我们将讨论 RNN 的主要概念。我们将从查看典型结构开始一个RNN，它包括一个用于对序列数据建模的递归组件。然后，我们将研究如何在典型的 RNN 中计算神经元激活。这将为我们讨论训练 RNN 中的常见挑战创造一个背景，然后我们将讨论这些挑战的解决方案，例如 LSTM和门控循环单元（GRU）。

理解 RNN 中的数据流

让我们从RNN 的架构。图 15.3并排显示了标准前馈 NN 和 RNN 中的数据流以进行比较：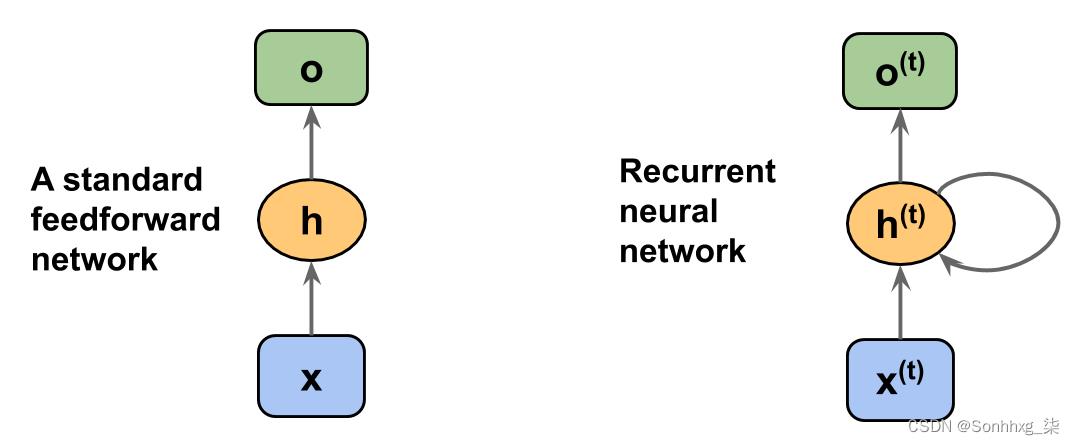

图 15.3：标准前馈 NN 和 RNN 的数据流

这两个网络都只有一个隐藏层。在此表示中，不显示单元，但我们假设输入层 ( x )、隐藏层 ( h ) 和输出层 ( o ) 是包含许多单元的向量。

确定 RNN 的输出类型

这种通用的 RNN 架构可以对应于输入是序列的两个序列建模类别。通常，循环层可以返回一个序列作为输出，或者简单地返回最后一个输出（在t  =  T处，即o ( T )）。因此，它可以是多对多的，也可以是多对一的，例如，如果我们只使用最后一个元素o ( T )作为最终输出。

稍后我们将在 PyTorch 模块中看到这是如何处理的torch.nn，当我们详细了解循环层在将序列作为输出返回时的行为时。

在一个标准前馈网络，信息从输入流向隐藏层，然后从隐藏层流向输出层。另一方面，在 RNN 中，隐藏层从当前时间步的输入层和前一个时间步的隐藏层接收其输入。

隐藏层中相邻时间步长的信息流使网络能够记忆过去的事件。这种信息流通常显示为一个循环，也称为循环作为图形符号中的循环边，这就是这种通用 RNN 架构的名称。

与多层感知器类似，RNN 可以由多个隐藏层组成。请注意，将具有一个隐藏层的 RNN 称为单层 RNN是一种常见的约定，不要与没有隐藏层的单层 NN 混淆，例如 Adaline 或逻辑回归。图 15.4展示了一个带有一个隐藏层（顶部）的 RNN 和一个带有两个隐藏层（底部）的 RNN：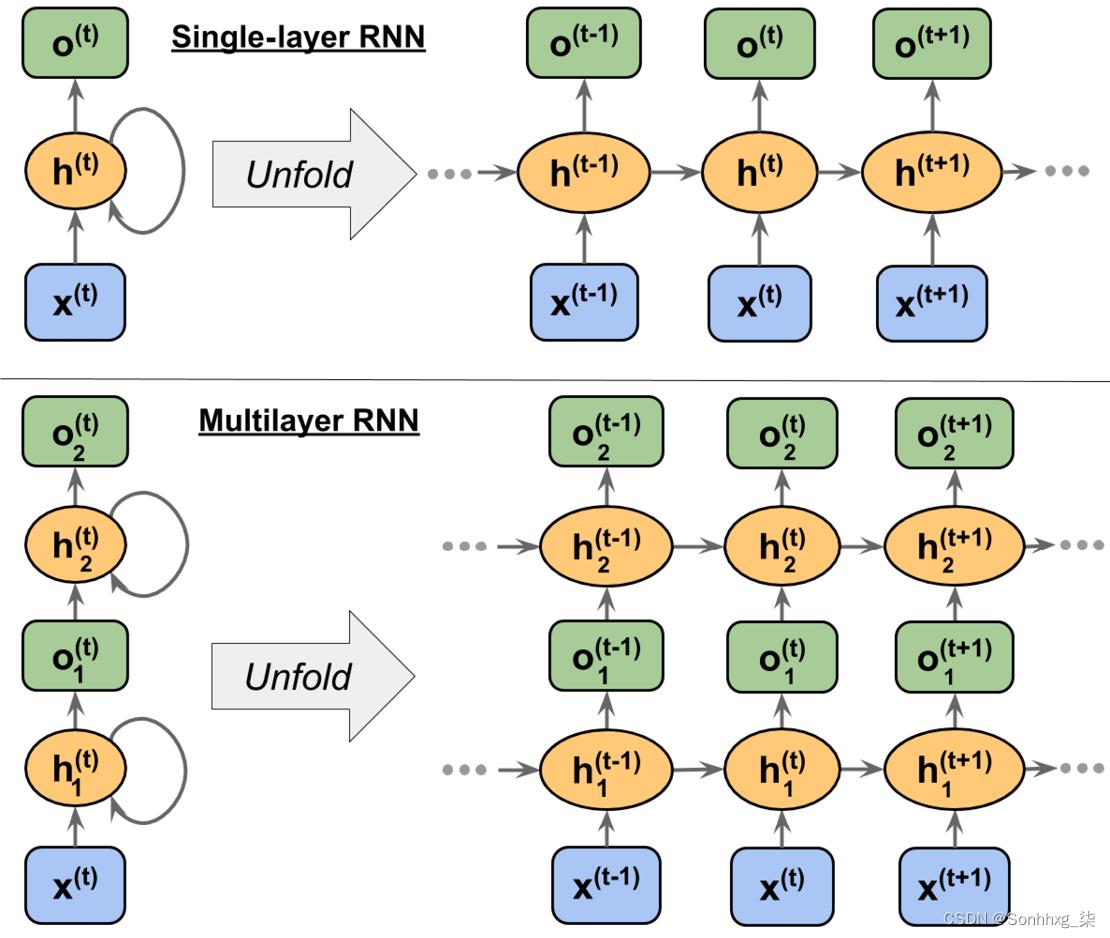

图 15.4：具有一个和两个隐藏层的 RNN 示例

检查RNN 的架构和信息流，可以展开具有循环边的紧凑表示，如图 15.4 所示。

众所周知，标准 NN 中的每个隐藏单元只接收一个输入——与输入层相关的网络预激活。相比之下，RNN 中的每个隐藏单元都接收两组不同的输入——来自输入层的预激活和来自上一个时间步t  – 1 的相同隐藏层的激活。

在第一个时间步，t  = 0，隐藏单元被初始化为零或小的随机值。然后，在t  > 0 的时间步，隐藏单元从当前时间的数据点x ( t )接收它们的输入，以及隐藏单元在t  – 1 处的先前值，表示为h ( t –1 ) .

同样，在多层 RNN 的情况下，我们可以将信息流总结如下：

• layer  = 1：这里，隐藏层表示为

  

  ，它接收来自数据点x ( t )的输入，以及同一层中的隐藏值，但在前一个时间步，。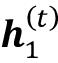
• layer  = 2：第二个隐藏层 ，在当前时间步（

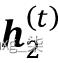
因为在这种情况下，每个循环层都必须接收一个序列作为输入，所以除了最后一个循环层之外的所有循环层都必须返回一个序列作为输出（也就是说，我们稍后必须设置return_sequences=True）。最后一个循环层的行为取决于问题的类型。

在 RNN 中计算激活

现在你了解RNN 中的结构和一般信息流，让我们更具体地计算隐藏层以及输出层的实际激活。为简单起见，我们只考虑一个隐藏层；然而，同样的概念也适用于多层 RNN。

我们刚刚看到的 RNN 表示中的每个有向边（框之间的连接）都与一个权重矩阵相关联。这些权重不依赖于时间t；因此，它们在时间轴上共享。单层RNN中不同的权重矩阵如下：

• W xh ：输入x ( t )和隐藏层h之间的权重矩阵
• W hh : 与循环边相关的权重矩阵
• Who :隐藏层和输出层之间的权重矩阵

这些权重矩阵如图 15.5 所示：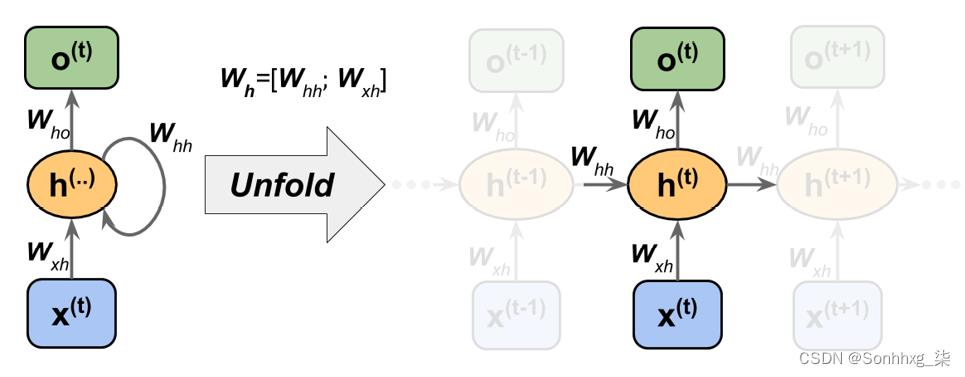

图 15.5：将权重应用于单层 RNN

在某些实现中，您可能会观察到权重矩阵W xh和W hh连接到组合矩阵W h  = [ W xh ; 嗯]。在本节的后面部分，我们也将使用这种表示法。

计算激活与标准多层感知器和其他类型的前馈神经网络非常相似。对于隐藏层，通过线性组合计算净输入z h（预激活）；也就是说，我们计算权重矩阵与相应向量的乘积之和，并添加偏置单元：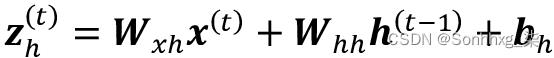

 然后，隐藏单元在时间步t的激活值计算如下：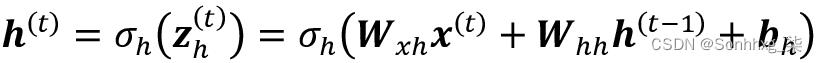

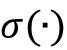
 这里，b h是隐藏的偏置向量单位

是隐藏层的激活函数。

如果您想使用连接的权重矩阵，W h  = [ W xh ; W hh ]，计算隐藏单元的公式会发生变化，如下：

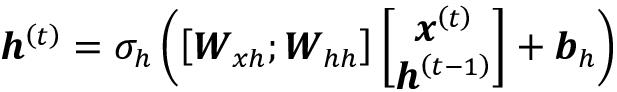
一旦计算了当前时间步的隐藏单元的激活，那么将计算输出单元的激活，如下所示：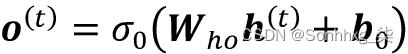

为了帮助进一步阐明这一点，图 15.6显示了使用两种公式计算这些激活的过程：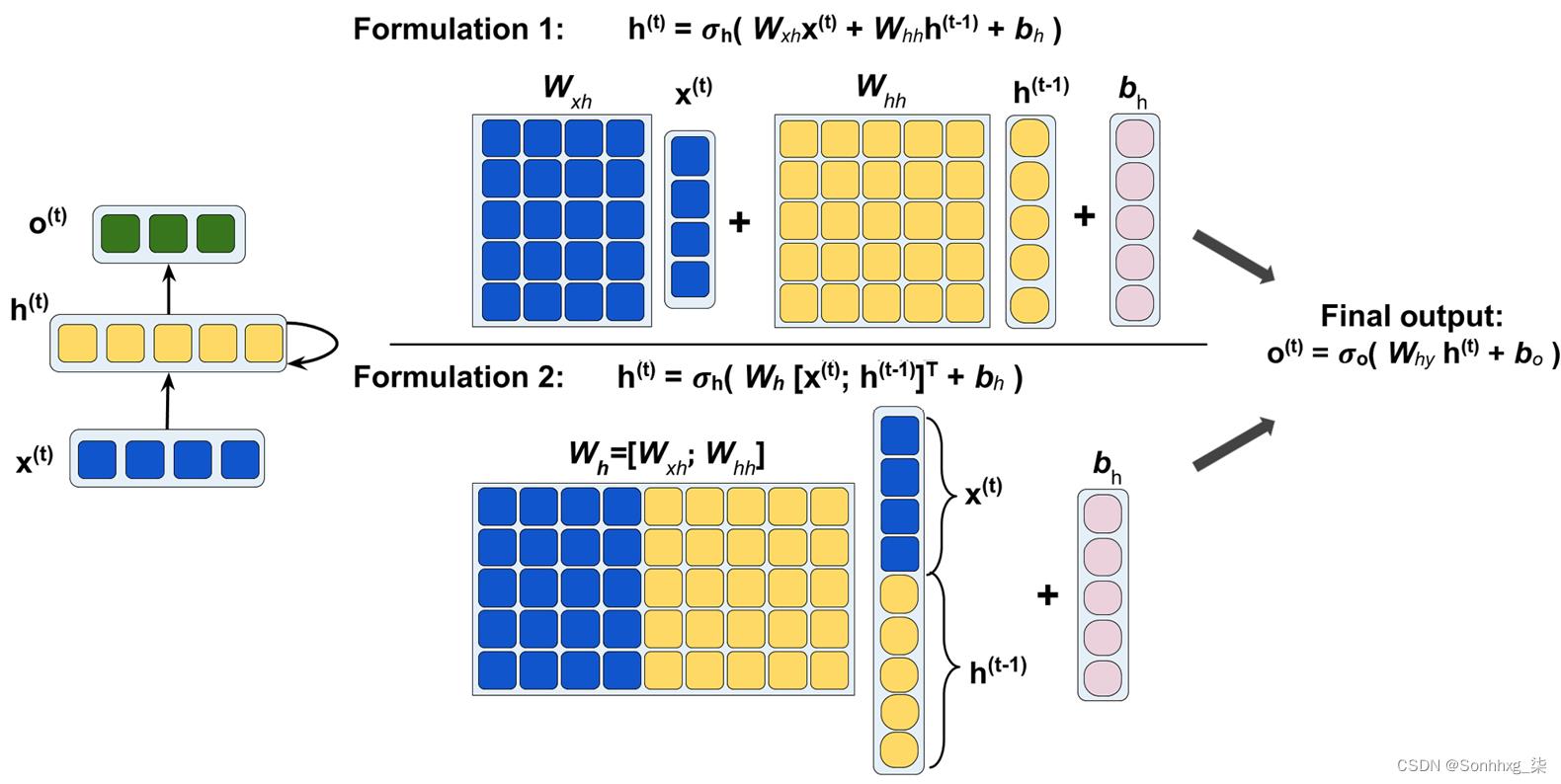

图 15.6：计算激活

使用随时间的反向传播 (BPTT) 训练 RNN

RNN 的学习算法是在 1990 年引入的：Backpropagation Through Time: What It does and How to Do ( Paul Werbos , Proceedings of IEEE , 78(10): 1550-1560, 1990)。

梯度的推导可能有点复杂，但基本思想是总损失L是时间t  = 1 到t  =  T的所有损失函数的总和：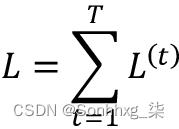

 由于时间t的损失取决于所有先前时间步骤 1 :  t的隐藏单元，因此梯度将按如下方式计算：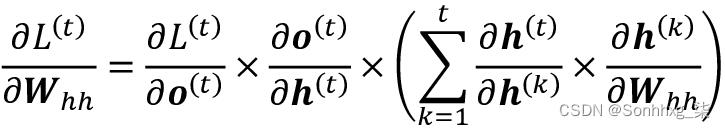

 在这里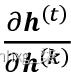，计算为相邻时间步长的乘积：

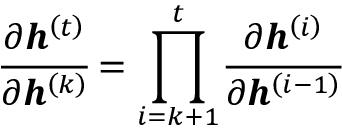
隐藏重复与输出重复

到目前为止，你已经看到循环网络，其中隐藏层具有循环性。但是，请注意，还有另一种模型，其中循环连接来自输出层。在这种情况下，可以通过以下两种方式之一添加上一个时间步的输出层的净激活值o t –1 ：

• 到当前时间步的隐藏层，h t（在图 15.7中显示为输出到隐藏的递归）
• 到当前时间步的输出层，o t（在图 15.7中显示为输出到输出的递归）

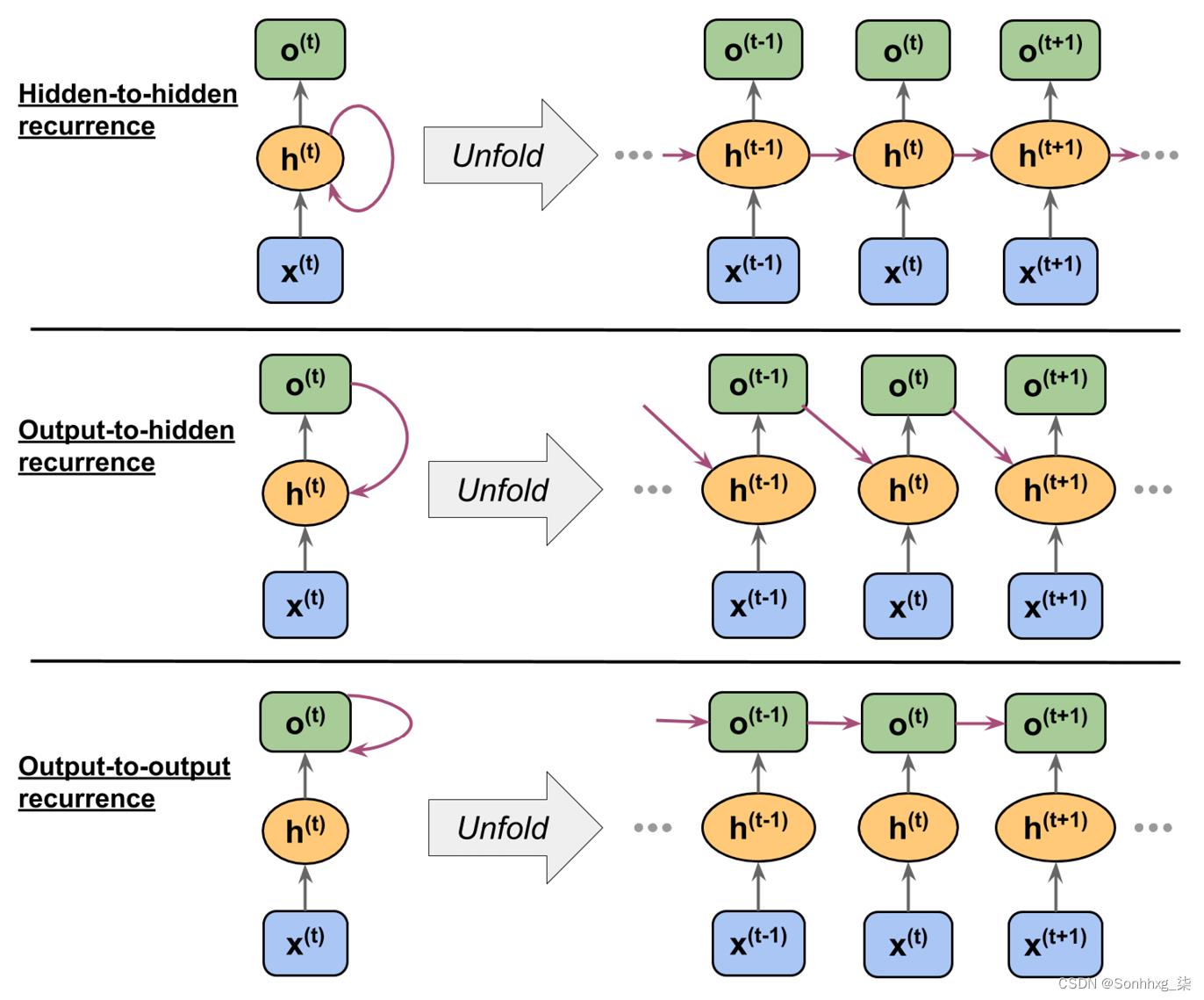
图 15.7：不同的循环连接模型

如图 15.7所示，这些架构之间的差异可以在重复连接中清楚地看到。按照我们的符号，与循环连接相关的权重将用W hh表示隐藏到隐藏的循环，用W oh表示输出到隐藏的循环，用W oo表示输出到输出的循环. 在一些文献中，与循环连接相关的权重也用W rec表示。

看看这个如何在实践中工作，让我们手动计算这些循环类型之一的前向传递。使用该torch.nn模块，可以通过定义循环层RNN，这类似于隐藏到隐藏的循环。在以下代码中，我们将从长度为 3 的输入序列创建循环层RNN并执行前向传递以计算输出。我们还将手动计算前向传递并将结果与RNN​​ .

首先，让我们创建层并为我们的手动计算分配权重和偏差：

>>> import torch
>>> import torch.nn as nn
>>> torch.manual_seed(1)
>>> rnn_layer = nn.RNN(input_size=5, hidden_size=2,
...                    num_layers=1, batch_first=True)
>>> w_xh = rnn_layer.weight_ih_l0
>>> w_hh = rnn_layer.weight_hh_l0
>>> b_xh = rnn_layer.bias_ih_l0
>>> b_hh = rnn_layer.bias_hh_l0
>>> print('W_xh shape:', w_xh.shape)
>>> print('W_hh shape:', w_hh.shape)
>>> print('b_xh shape:', b_xh.shape)
>>> print('b_hh shape:', b_hh.shape)
W_xh shape: torch.Size([2, 5])
W_hh shape: torch.Size([2, 2])
b_xh shape: torch.Size([2])
b_hh shape: torch.Size([2])

该层的输入形状是(batch_size, sequence_length, 5)，其中第一个维度是批量维度（我们设置batch_first=True），第二个维度对应于序列，最后一个维度对应于特征。请注意，我们将输出一个序列，其中，对于长度为 3 的输入序列将产生输出序列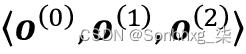。此外，RNN默认使用一层，您可以设置num_layers将多个 RNN 层堆叠在一起，形成一个堆叠的 RNN。

现在，我们将调用前向传递rnn_layer并手动计算每个时间步的输出并比较它们：

>>> x_seq = torch.tensor([[1.0]*5, [2.0]*5, [3.0]*5]).float()
>>> ## output of the simple RNN:
>>> output, hn = rnn_layer(torch.reshape(x_seq, (1, 3, 5)))
>>> ## manually computing the output:
>>> out_man = []
>>> for t in range(3):
...     xt = torch.reshape(x_seq[t], (1, 5))
...     print(f'Time step t =>')
...     print('   Input           :', xt.numpy())
...     
...     ht = torch.matmul(xt, torch.transpose(w_xh, 0, 1)) + b_hh
...     print('   Hidden          :', ht.detach().numpy()
...     
...     if t > 0:
...         prev_h = out_man[t-1]
...     else:
...         prev_h = torch.zeros((ht.shape))
...     ot = ht + torch.matmul(prev_h, torch.transpose(w_hh, 0, 1)) \\
...             + b_hh
...     ot = torch.tanh(ot)
...     out_man.append(ot)
...     print('   Output (manual) :', ot.detach().numpy())
...     print('   RNN output      :', output[:, t].detach().numpy())
...     print()
Time step 0 =>
   Input           : [[1. 1. 1. 1. 1.]]
   Hidden          : [[-0.4701929  0.5863904]]
   Output (manual) : [[-0.3519801   0.52525216]]
   RNN output      : [[-0.3519801   0.52525216]]
Time step 1 =>
   Input           : [[2. 2. 2. 2. 2.]]
   Hidden          : [[-0.88883156  1.2364397 ]]
   Output (manual) : [[-0.68424344  0.76074266]]
   RNN output      : [[-0.68424344  0.76074266]]
Time step 2 =>
   Input           : [[3. 3. 3. 3. 3.]]
   Hidden          : [[-1.3074701  1.886489 ]]
   Output (manual) : [[-0.8649416   0.90466356]]
   RNN output      : [[-0.8649416   0.90466356]]

在我们的手动前向计算中，我们使用了双曲正切 (tanh) 激活函数，因为它也用于RNN（默认激活）。从打印结果中可以看出，手动前向计算的输出与RNN每个时间步的层输出完全匹配。希望这项实践任务能够启发您了解循环网络的奥秘。

学习远程交互的挑战

BPTT，其中前面简要提到过，介绍了一些新的挑战。由于乘法因子 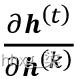，在计算损失函数的梯度时，会出现所谓的梯度消失和爆炸问题。

这些问题由图 15.8中的示例解释，为简单起见，它显示了一个只有一个隐藏单元的 RNN：

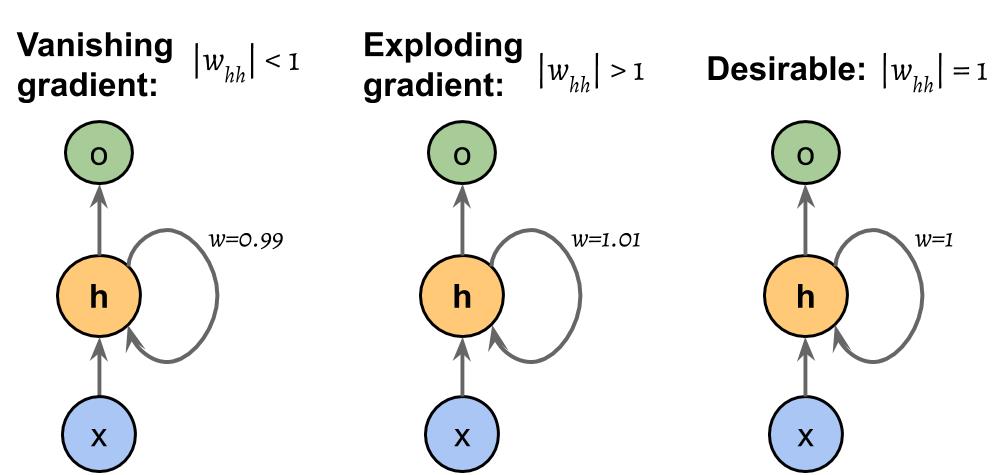
图 15.8：计算损失函数梯度的问题

基本上，

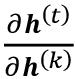
有t  –  k次乘法；因此，将权重w自身乘以t  –  k倍会得到一个因子w t – k。因此，如果 | w | < 1，当t  -  k很大时，这个因素变得非常小。另一方面，如果循环边的权重为 | w | > 1，则当t  -  k很大时， w t - k变得非常大。请注意，大的t  –  k指的是长期依赖。我们可以看到，通过确保 | 可以达到避免梯度消失或爆炸的简单解决方案。w | = 1. 如果您有兴趣并想对此进行更多调查详细信息，请阅读R. Pascanu、T. Mikolov和Y. Bengio的关于训练递归神经网络的难度，2012 年 ( https://arxiv.org/pdf/1211.5063.pdf )。

在实践中，这个问题至少有三种解决方案：

• 渐变剪裁
• 随时间截断的反向传播( TBPTT )
• 长短期记忆体

使用梯度裁剪，我们为梯度指定一个截止值或阈值，并将这个截止值分配给超过这个值的梯度值。相比之下，TBPTT 只是限制了信号在每次前向传播后可以反向传播的时间步数。例如，即使序列有 100 个元素或步长，我们也可能只反向传播最近的 20 个时间步长。

虽然渐变剪裁和TBPTT可以解决爆炸梯度问题，截断限制了梯度可以有效回流并正确更新权重的步数。另一方面，由 Sepp Hochreiter 和 Jürgen Schmidhuber 于 1997 年设计的 LSTM 在通过使用存储单元对长程依赖性进行建模的同时，更成功地解决了梯度消失和爆炸问题。让我们更详细地讨论 LSTM。

长短期记忆细胞

如前所述，LSTM 是首次引入以克服梯度消失问题（S. Hochreiter和J. Schmidhuber的Long Short-Term Memory，Neural Computation，9(8): 1735-1780, 1997）。一个构建块LSTM 是一个记忆单元，它本质上代表或替代了标准 RNN 的隐藏层。

正如我们所讨论的，在每个存储单元中，都有一个具有理想权重w  = 1 的循环边，以克服梯度消失和爆炸的问题。与此循环边相关联的值统称为称为细胞状态。现代 LSTM 单元的展开结构如图 15.9所示：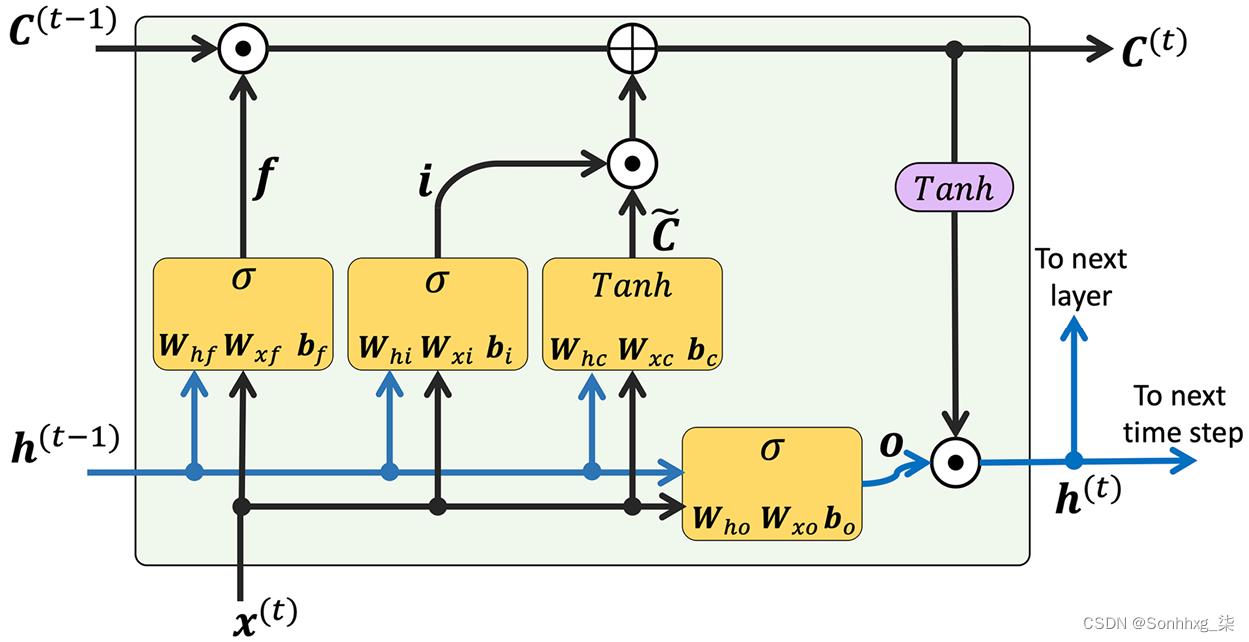

图 15.9：LSTM 单元的结构

请注意，前一个时间步长的细胞状态C ( t –1)被修改以获取当前时间步长C ( t )的细胞状态，而无需直接乘以任何权重因子。这个存储单元中的信息流由几个计算单元（通常称为门）控制，这些计算单元将被描述here。图中，

指逐元素乘积（逐元素乘法），表示逐元素求和（逐元素加法）。此外，x ( t )指的是输入数据时间t和h ( t –1)表示时间t  – 1 的隐藏单元。四个框用激活函数表示，或者是 sigmoid 函数 ( ) 或 tanh，以及一组权重；这些框通过对其输入（即h ( t –1)和x ( t )）执行矩阵向量乘法来应用线性组合。这些使用 sigmoid 的计算单元激活函数，其输出单元通过，是称为门。

在 LSTM 单元中，存在三种不同类型的门，称为遗忘门、输入门和输出门：

遗忘门( f t )允许存储单元重置单元状态而不会无限增长。事实上，遗忘门决定了哪些信息可以通过，哪些信息可以抑制。现在，f t计算如下：

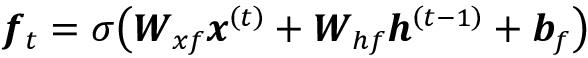
请注意，遗忘门不是原始 LSTM 单元的一部分；几年后它被添加以改进原始模型（学习忘记：F. Gers、J. Schmidhuber和F. Cummins的LSTM 连续预测，神经计算 12 , 2451-2471, 2000）。

输入门( i t )和候选值( 

) 负责用于更新细胞状态。它们被计算为如下：

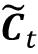
时间t的单元状态计算如下：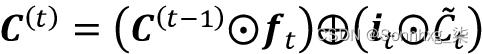

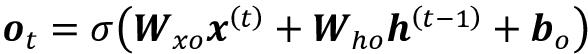
输出门( o t )决定如何更新隐藏单元的值：

鉴于此，当前时间步的隐藏单元计算如下：

一个结构LSTM 单元及其底层计算可能看起来非常复杂且难以实现。然而，好消息是 PyTorch 已经在优化的包装函数中实现了所有内容，这使我们能够轻松有效地定义 LSTM 单元。我们将在本章后面将 RNN 和 LSTM 应用于现实世界的数据集。

其他高级 RNN 模型

LSTM 为序列中的远程依赖关系建模提供了一种基本方法。然而，重要的是要注意文献中描述的 LSTM 的许多变体（Rafal Jozefowicz、Wojciech Zaremba和Ilya Sutskever的循环网络架构的实证探索，ICML 会议记录，2342-2350，2015）。另外值得注意的是一种更新的方法，门控循环单元( GRU )，它于 2014 年提出。GRU 的架构比 LSTM 更简单；因此，它们的计算效率更高，而它们在某些任务（例如和弦音乐建模）中的性能可与 LSTM 相媲美。如果您有兴趣了解有关这些现代 RNN 架构的更多信息，请参阅Junyoung Chung等人在序列建模上的门控循环神经网络的实证评估，2014 年 ( https://arxiv.org/pdf/1412.3555v1.pdf）。

在 PyTorch 中为序列建模实现 RNN

现在我们有了涵盖了背后的基本理论RNN，我们准备好进入本章更实用的部分：在 PyTorch 中实现 RNN。在本章的其余部分，我们将把 RNN 应用于两个常见的问题任务：

1. 情绪分析
2. 语言建模

这两个项目，我们将在接下来的几页中一并介绍，它们既引人入胜，也相当投入。因此，我们不会一次提供所有代码，而是将实现分成几个步骤并详细讨论代码。如果您想在深入讨论之前有一个全面的概览并希望一次查看所有代码，请先查看代码实现。

项目一——预测IMDb电影评论的情绪

您可能还记得第 8 章，将机器学习应用于情感分析，情感分析涉及分析句子或文本文档的表达意见。在本节和以下小节中，我们将实现一个多层 RNN使用多对一架构的情感分析。

在下一节中，我们将为语言建模应用实现多对多 RNN。虽然选择的示例有意简单地介绍 RNN 的主要概念，但语言建模具有广泛的有趣应用，例如构建聊天机器人——使计算机能够直接与人类交谈和交互。

准备电影评论数据

在第 8 章中，我们预处理和清理评论数据集。我们现在也会这样做。首先，我们将导入必要的模块并从中读取数据torchtext（我们将通过 安装pip install torchtext；截至 2021 年底使用的是 0.10.0 版），如下所示：

>>> from torchtext.datasets import IMDB
>>> train_dataset = IMDB(split='train')
>>> test_dataset = IMDB(split='test')

每组有 25,000 个样本。数据集的每个样本都包含两个元素，代表我们要预测的目标标签的情感标签（neg指的是负面情绪和pos指的是正面情绪），以及电影评论文本（输入特征）。这些电影评论的文本组件是单词序列，RNN 模型将每个序列分类为正面 ( 1) 或负面 ( 0) 评论。

然而，在我们将数据输入 RNN 模型之前，我们需要应用几个预处理步骤：

1. 将训练数据集拆分为单独的训练和验证分区。
2. 识别训练数据集中的唯一词
3. 将每个唯一单词映射到唯一整数，并将评论文本编码为编码整数（每个唯一单词的索引）
4. 将数据集划分为小批量作为模型的输入

让我们继续第一步：根据train_dataset我们之前阅读的内容创建一个训练和验证分区：

>>> ## Step 1: create the datasets
>>> from torch.utils.data.dataset import random_split
>>> torch.manual_seed(1)
>>> train_dataset, valid_dataset = random_split(
...     list(train_dataset), [20000, 5000])

原始训练数据集包含 25,000 个示例。随机选择 20,000 个样本进行训练，5,000 个样本进行验证。

为了准备输入到 NN 的数据，我们需要将其编码为数值，如步骤 2和3中所述。为此，我们将首先在训练数据集中找到唯一的词（标记）。虽然找到唯一标记是我们可以使用 Python 数据集的过程，但使用包中的Counter类会更有效collections，它是 Python 标准库的一部分。

在下面的代码中，我们将实例化一个新Counter对象 ( token_counts)，该对象将收集唯一的词频。请注意，在这个特定的应用程序中（与词袋模型相反），我们只对唯一词集感兴趣，而不需要作为副产品创建的词数。要将文本拆分为单词（或标记），我们将重用tokenizer我们在第 8 章中开发的函数，该函数还删除了 html 标记以及标点符号和其他非字母字符：

收集唯一令牌的代码如下：

>>> ## Step 2: find unique tokens (words)
>>> import re
>>> from collections import Counter, OrderedDict
>>> 
>>> def tokenizer(text):
...     text = re.sub('<[^>]*>', '', text)
...     emoticons = re.findall(
...         '(?::|;|=)(?:-)?(?:\\)|\\(|D|P)', text.lower()
...     )
...     text = re.sub('[\\W]+', ' ', text.lower()) +\\
...         ' '.join(emoticons).replace('-', '')
...     tokenized = text.split()
...     return tokenized
>>> 
>>> token_counts = Counter()
>>> for label, line in train_dataset:
...     tokens = tokenizer(line)
...     token_counts.update(tokens)
>>> print('Vocab-size:', len(token_counts))
Vocab-size: 69023

如果您想了解更多关于的信息，请参阅collections — Container datatypes — Python 3.10.7 documentationCounter上的文档。

接下来，我们是将每个唯一的单词映射到一个唯一的整数。这可以使用 Python 字典手动完成，其中键是唯一标记（单词），与每个键关联的值是唯一整数。但是，该torchtext包已经提供了一个类 ，Vocab我们可以使用它来创建这样的映射并对整个数据集进行编码。首先，我们将vocab通过将有序字典映射标记传递给它们对应的出现频率来创建一个对象（有序字典是 sorted token_counts）。其次，我们将在词汇表中添加两个特殊标记——填充和未知标记：

>>> ## Step 3: encoding each unique token into integers
>>> from torchtext.vocab import vocab
>>> sorted_by_freq_tuples = sorted(
...     token_counts.items(), key=lambda x: x[1], reverse=True
... )
>>> ordered_dict = OrderedDict(sorted_by_freq_tuples)
>>> vocab = vocab(ordered_dict)
>>> vocab.insert_token("<pad>", 0)
>>> vocab.insert_token("<unk>", 1)
>>> vocab.set_default_index(1)

为了演示如何使用该vocab对象，我们将示例输入文本转换为整数值列表：

>>> print([vocab[token] for token in ['this', 'is',
...     'an', 'example']])
[11, 7, 35, 457]

请注意，验证或测试数据中可能有一些标记不存在于训练数据中，因此不包含在映射中。如果我们有q个标记（即token_counts传递给的大小Vocab，在本例中为 69,023），那么之前未见过的所有标记，因此未包含在 中token_counts，将被分配整数 1（占位符对于未知令牌）。换句话说，索引 1 是为未知词保留的。另一个保留值是整数 0，它用作占位符，即所谓的填充标记，用于调整序列长度。稍后，当我们在 PyTorch 中构建 RNN 模型时，我们将更详细地考虑这个占位符 0。

我们可以定义text_pipeline函数来相应地转换数据集中的每个文本，以及label_pipeline将每个标签转换为 1 或 0 的函数：

>>> ## Step 3-A: define the functions for transformation
>>> text_pipeline =\\
...      lambda x: [vocab[token] for token in tokenizer(x)]
>>> label_pipeline = lambda x: 1. if x == 'pos' else 0.

我们将使用先前声明的数据处理管道生成批量样本DataLoader并将其传递给参数collate_fn。我们将文本编码和标签转换函数包装到collate_batch函数中：

 ## Step 3-B: wrap the encode and transformation function
... def collate_batch(batch):
...     label_list, text_list, lengths = [], [], []
...     for _label, _text in batch:
...         label_list.append(label_pipeline(_label))
...         processed_text = torch.tensor(text_pipeline(_text),
...                                       dtype=torch.int64)
...         text_list.append(processed_text)
...         lengths.append(processed_text.size(0))
...     label_list = torch.tensor(label_list)
...     lengths = torch.tensor(lengths)
...     padded_text_list = nn.utils.rnn.pad_sequence(
...         text_list, batch_first=True)
...     return padded_text_list, label_list, lengths
>>> 
>>> ## Take a small batch
>>> from torch.utils.data import DataLoader
>>> dataloader = DataLoader(train_dataset, batch_size=4,
...                         shuffle=False, collate_fn=collate_batch)

到目前为止，我们已经将单词序列转换为整数序列，将 or 的标签pos转换neg为 1 或 0。但是，我们需要解决一个问题 - 序列当前具有不同的长度（如执行结果所示以下代码为四个示例）。尽管通常 RNN 可以处理不同长度的序列，但我们仍然需要确保 mini-batch 中的所有序列都具有相同的长度，以便将它们有效地存储在张量中。

PyTorch提供了一种有效的方法，pad_sequence()它会自动使用占位符值 (0) 填充要组合到批次中的连续元素，以便批次中的所有序列都具有相同的形状。在前面的代码中，我们已经从训练数据集中创建了一个小批量的数据加载器并应用了该collate_batch函数，该函数本身包含一个pad_sequence()调用。

但是，为了说明填充的工作原理，我们将获取第一批并打印各个元素的大小，然后再将它们组合成小批量，以及生成的小批量的尺寸：

>>> text_batch, label_batch, length_batch = next(iter(dataloader))
>>> print(text_batch)
tensor([[   35,  1742,     7,   449,   723,     6,   302,     4,
...
0,     0,     0,     0,     0,     0,     0,     0]],
>>> print(label_batch)
tensor([1., 1., 1., 0.])
>>> print(length_batch)
tensor([165,  86, 218, 145])
>>> print(text_batch.shape)
torch.Size([4, 218])

从打印的张量形状中可以看出，第一批的列数为 218，这是将前四个示例组合成一个批次并使用这些示例的最大大小的结果。这意味着该批次中的其他三个示例（其长度分别为 165、86 和 145）将根据需要填充以匹配此大小。

最后，让我们将所有三个数据集划分为批量大小为 32 的数据加载器：

>>> batch_size = 32
>>> train_dl = DataLoader(train_dataset, batch_size=batch_size,
...                       shuffle=True, collate_fn=collate_batch)
>>> valid_dl = DataLoader(valid_dataset, batch_size=batch_size,
...                       shuffle=False, collate_fn=collate_batch)
>>> test_dl = DataLoader(test_dataset, batch_size=batch_size,
...                      shuffle=False, collate_fn=collate_batch)

现在，数据的格式适合 RNN 模型，我们将在以下小节中实现。然而，在下一小节中，我们将首先讨论特征嵌入，这是一个可选但强烈推荐的预处理步骤，用于降低词向量的维数。

用于句子编码的嵌入层

在此期间在上一步的数据准备中，我们生成了相同长度的序列。这些序列的元素是对应于唯一词索引的整数。这些词索引可以通过几种不同的方式转换为输入特征。一种天真的方法是应用 one-hot 编码将索引转换为 0 和 1 的向量。然后，每个词将被映射到一个向量，其大小是整个数据集中唯一词的数量。鉴于唯一词的数量（词汇表的大小）可以在 10 4  – 10 5的数量级，这也将是数字在我们的输入特征中，在这些特征上训练的模型可能会遭受维度灾难。此外，这些特征非常稀疏，因为除了一之外都为零。

一种更优雅的方法是将每个单词映射到具有实值元素（不一定是整数）的固定大小的向量。与 one-hot 编码向量相比，我们可以使用有限大小的向量来表示无限数量的实数。（