创作赢红包＜ 二叉树OJ题 ＞单值二叉树&&二叉树的最大深度&&翻转二叉树&&相同的树&&对称二叉树

Posted Sherry的成长之路

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了创作赢红包＜ 二叉树OJ题 ＞单值二叉树&&二叉树的最大深度&&翻转二叉树&&相同的树&&对称二叉树相关的知识，希望对你有一定的参考价值。

​

​📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：数据结构
🎯长路漫漫浩浩，万事皆有期待

文章目录

二叉树OJ练习(一)

1. 单值二叉树

链接：单值二叉树
题述：如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 1：
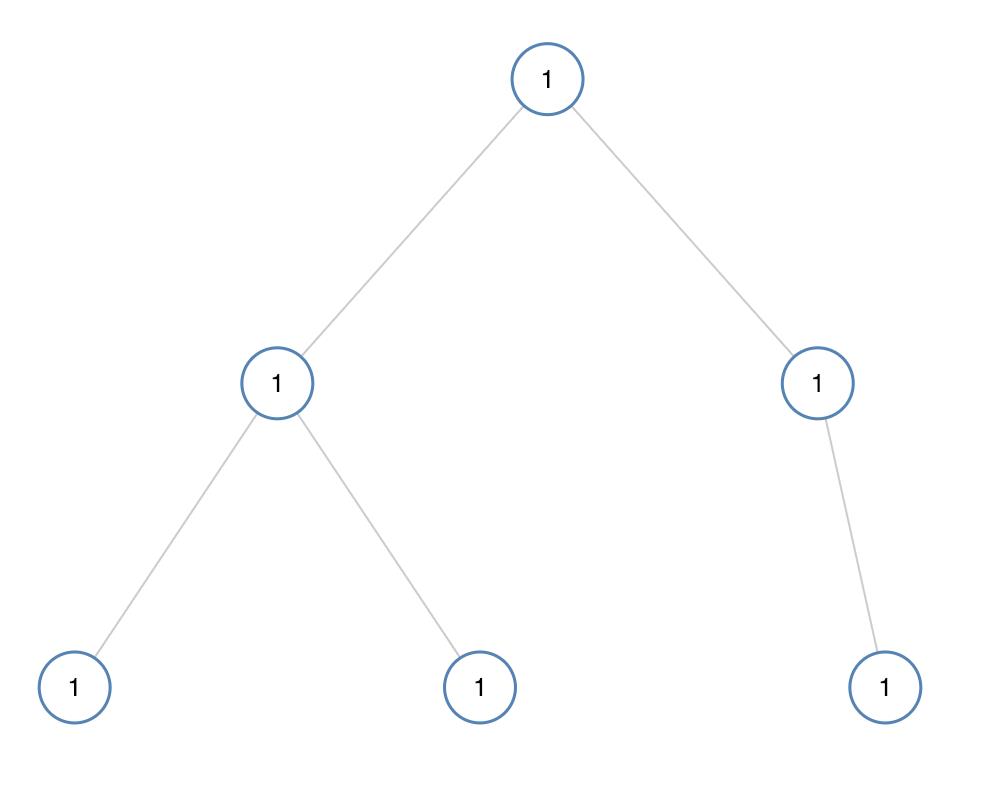
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：
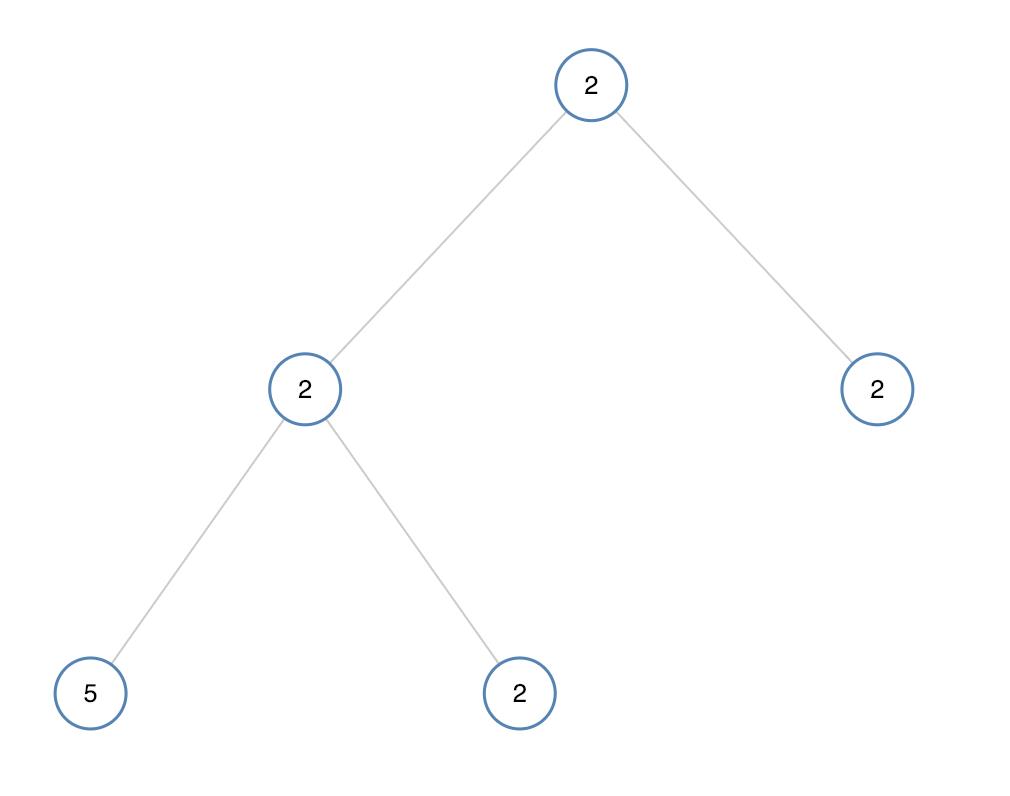
输入：[2,2,2,5,2]
输出：false

提示：
两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

核心思想：

在数学中大家都知道等号具有传递性，如 a = b , b = c，那么 a = c 。那么这里
a == b && a == c
b == d && b == e
… …

思路：
判断两棵树是否相等，我们先思考一下如何才算相等：

1.对于 两棵空树 ，必定相等，返回真；
2.如果 一棵树空，另一棵树不为空 ，那么不相等，返回假
3.如果 树中值相同但是结构不同 ，那么也不相等，返回假；
4.如果 两棵树对应节点的值不相等，那么也不相等，返回假；

那么只要分别递归两棵的左右子树，如果一直递归到底都是真，且左右子树返回的结果都为真，那么这两棵树就相同。

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

typedef int BTDataType;
typedef struct TreeNode 

	int val;
	struct TreeNode *left;
	struct TreeNode *right;
BTNode;
//单值二叉树
bool isUnivalTree(struct TreeNode* root) 
	if (root == NULL)
	
		return true;
	
	//左树不为空且左树不等于根val
	if (root->left && root->left->val != root->val)
	
		return false;		
	
	//右树不为空且右树不等于根val
	if (root->right && root->right->val != root->val)
	
		return false;
	
	//递归
	return isUnivalTree(root->left) && isUnivalTree(root->right);

//malloc空间
BTNode* BuyNode(BTDataType x)

	BTNode* node = malloc(sizeof(BTNode));
	node->val = x;
	node->left = NULL;
	node->right = NULL;

	return node;

//创建树
BTNode* CreatBinaryTree()

	BTNode* node1 = BuyNode('A');
	BTNode* node2 = BuyNode('A');
	BTNode* node3 = BuyNode('A');
	BTNode* node4 = BuyNode('A');
	BTNode* node5 = BuyNode('A');
	BTNode* node6 = BuyNode('A');

	node1->left = node2;
	node1->right = node3;
	node2->left = node4;
	node2->right = node5;
	node3->right = node6;

	return node1;


int main()

	BTNode* root = CreatBinaryTree();
	printf("%d\\n", isUnivalTree(root));
	return 0;

2. 二叉树的最大深度

链接：二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例：

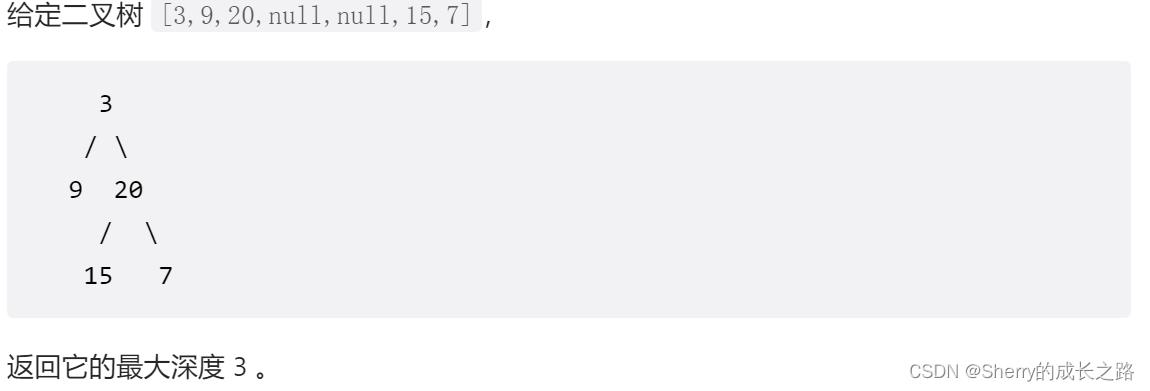
思路：与上一篇博客中求树的高度/深度同理

int maxDepth(struct TreeNode* root)

    if (root == NULL)
	
		return 0;
	
	int leftDepth = maxDepth(root->left);
	int rightDepth = maxDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;

3. 翻转二叉树

链接：226. 翻转二叉树

描述：给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

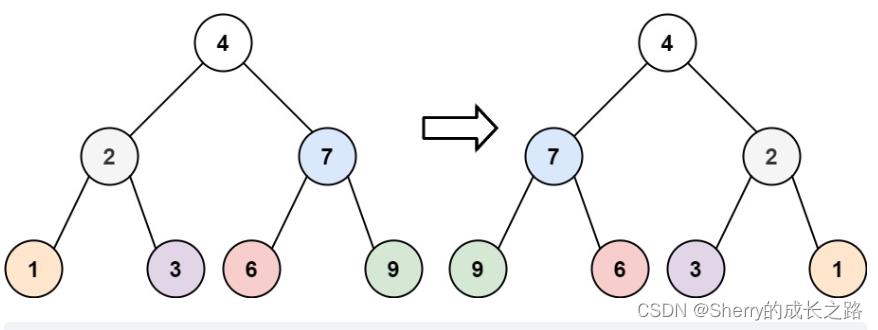
示例1：
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

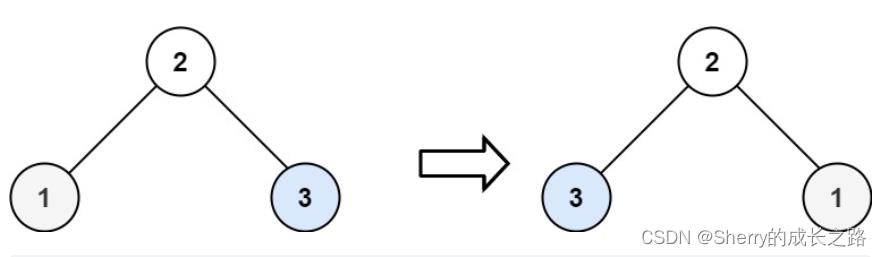
示例2：
输入：root = [2,1,3]
输出：[2,3,1]

示例3：

输入：root = []
输出：[]

提示：
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

思路：对于翻转二叉树，就是把一棵树所有的左右子树对调，这里我们可以使用后序遍历的思想。

那么我们基本就可以写出我们的思路：
如果节点为空，那么无需翻转，返回 NULL；
否则就先递归左子树，再递归右子树，到底后，开始交换左右子树，最后逐层返回。

struct TreeNode* invertTree(struct TreeNode* root)

    //如果root为空，直接返回
    if(root==NULL)
    
        return NULL;
    
    //使用后序遍历的思想，找到最好的左右子树
    //交换他们的左右孩子

    //记录值，防止重复递归
    struct TreeNode*left=invertTree(root->left);
    struct TreeNode*right=invertTree(root->right);

    root->left=right;
    root->right=left;
    //每次递归返回的就是翻转后的子树
    return root;

4. 相同的树

链接：100. 相同的树

描述：
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

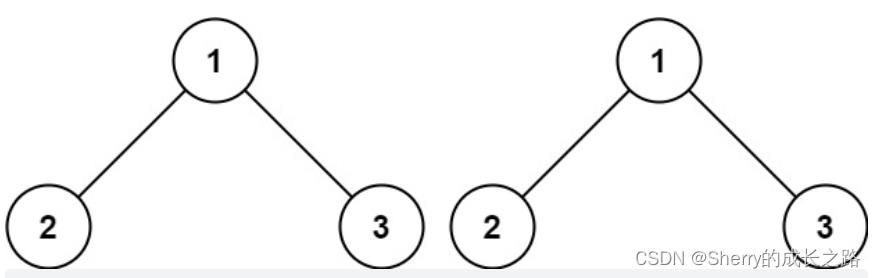
示例 1：
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：
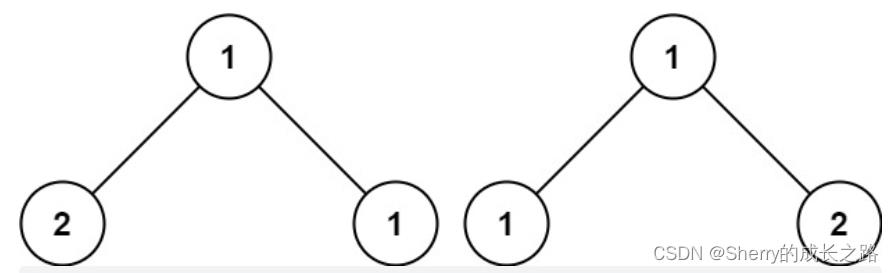
输入：p = [1,2,1], q = [1,1,2]
输出：false

注意：
两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

核心思想：在递归时每一层函数的栈帧中存在这样的条件：p 为空，q 也为空，返回 true；p 或者 q 只有一个为空，返回 false；p 和 q 的 val 不等，返回 false；否则 p 和 q 的 val 是相等的才递归

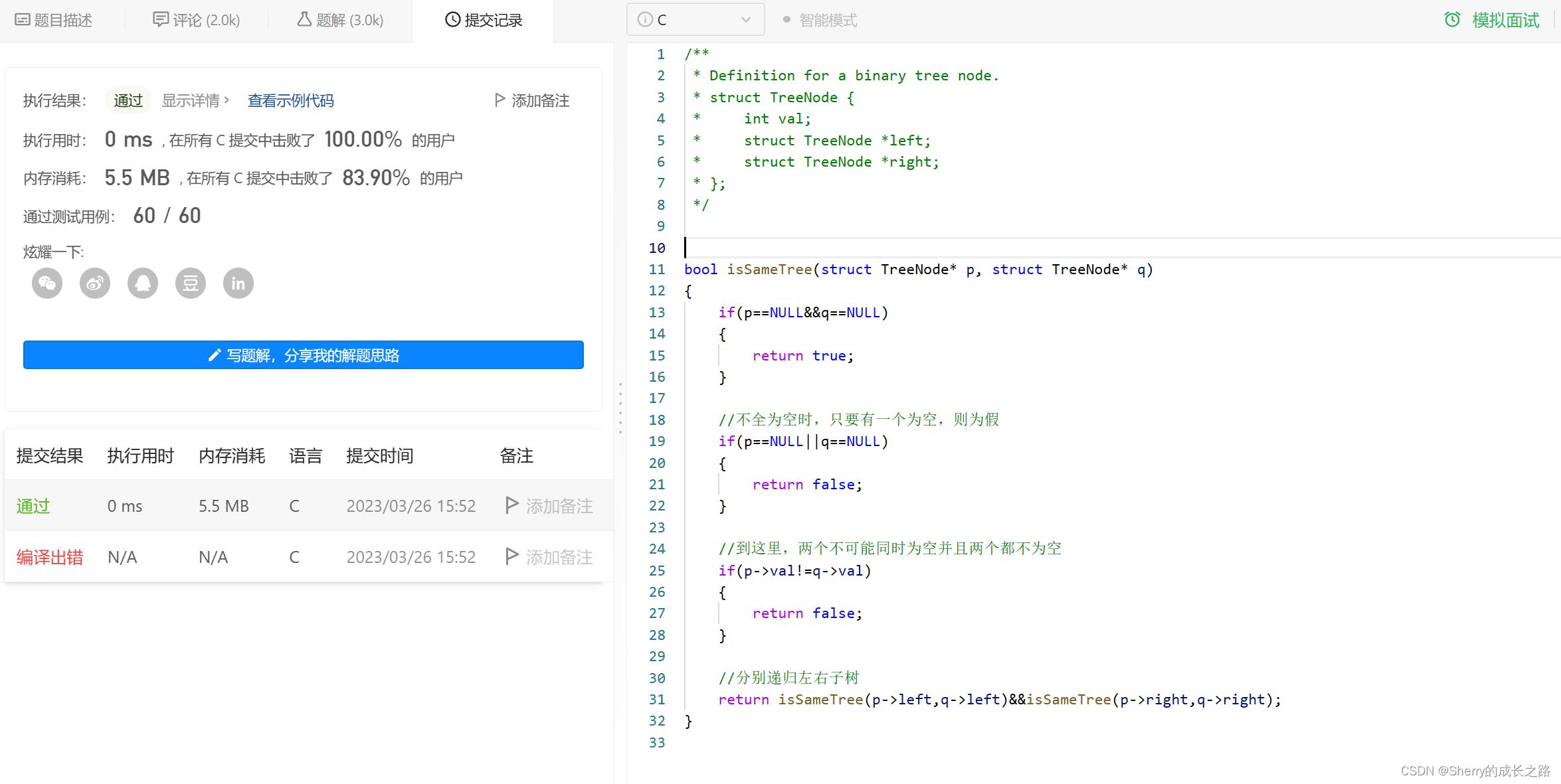
bool isSameTree(struct TreeNode* p, struct TreeNode* q)

	//都为空
    if(p==NULL&&q==NULL)
    
        return true;
    

    //走的这里，至少有一个不为空，不全为空时，只要有一个为空，则为假
    if(p==NULL||q==NULL)
    
        return false;
    

    //到这里，两个都不为空，且两个都不相等，为假
    if(p->val!=q->val)
    
        return false;
    
    
	//到这里，两个都不为空，且两个相等
    //分别比较，递归左右子树
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);

5. 对称二叉树

链接：101. 对称二叉树

描述：给你一个二叉树的根节点 root ， 检查它是否轴对称。

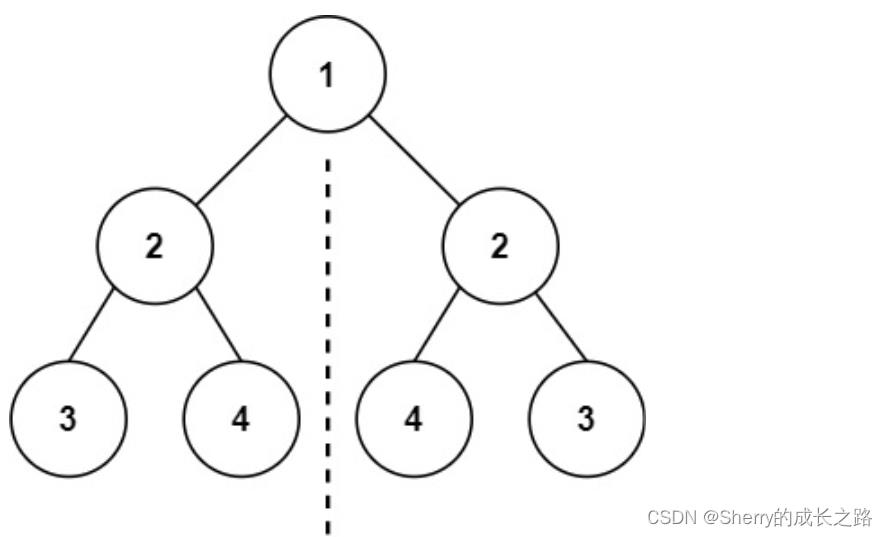
示例 1：
[1,2,2,3,4,4,3] 是镜像对称的

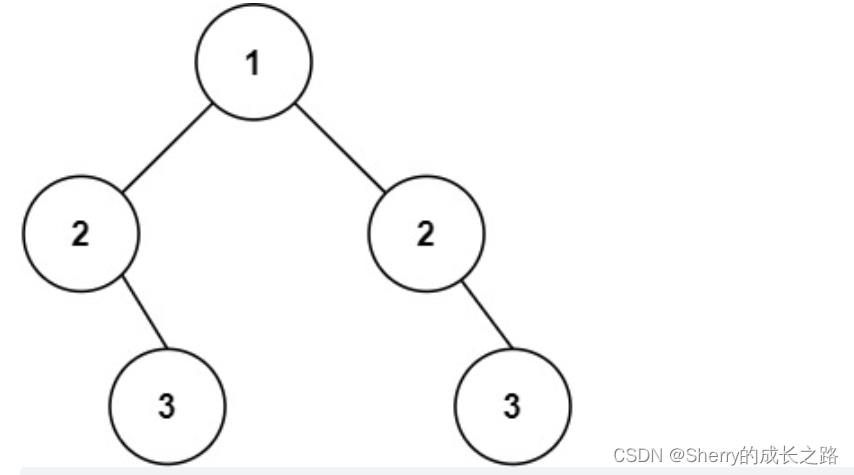
示例 2：
[1,2,2,null,3,null,3] 则不是镜像对称的

思路1：

一棵树是否轴对称，可以理解为它的根节点的某一边子树翻转后是否和另一边为相同的树。

我们上方相同的树和翻转二叉树刚刚写过，那么写这种思路就很简单了。

如果左右子树都为空，为根节点，那么返回真；
如果左右子树一边不为空，那么返回假；
如果左右子树都不为空，那么给定 left 和 right 分别记录左右子树。翻转左边，记录右边；
最后返回判断左右子树是否为相同的树。

struct TreeNode* invertTree(struct TreeNode* root)

    //如果root为空，直接返回
    if(root==NULL)
    
        return NULL;
    
    //使用后序遍历的思想，找到最好的左右子树
    //交换他们的左右孩子

    //记录值，防止重复递归
    struct TreeNode*left=invertTree(root->left);
    struct TreeNode*right=invertTree(root->right);

    root->left=right;
    root->right=left;
    //每次递归返回的就是翻转后的子树
    return root;


bool isSameTree(struct TreeNode* p, struct TreeNode* q)

    if(p==NULL&&q==NULL)
    
        return true;
    

    //不全为空时，只要有一个为空，则为假
    if(p==NULL||q==NULL)
    
        return false;
    

    //到这里，两个不可能同时为空并且两个都不为空
    if(p->val!=q->val)
    
        return false;
    
    //分别递归左右子树
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);



bool isSymmetric(struct TreeNode* root)

    //左右子树都为空
    if(root->left==NULL&&root->right==NULL)
    
        return true;
    

    //左右子树一边不为空
    if(root->left==NULL||root->right==NULL)
    
        return false;
    

    //左右子树两边都不为空
    struct TreeNode*left,*right;
    if(root->left&&root->right)
    
        //翻转左边
        left=invertTree(root->left);
        right=root->right;
    

    //和右边子树比较，返回bool值
    return isSameTree(left,right);

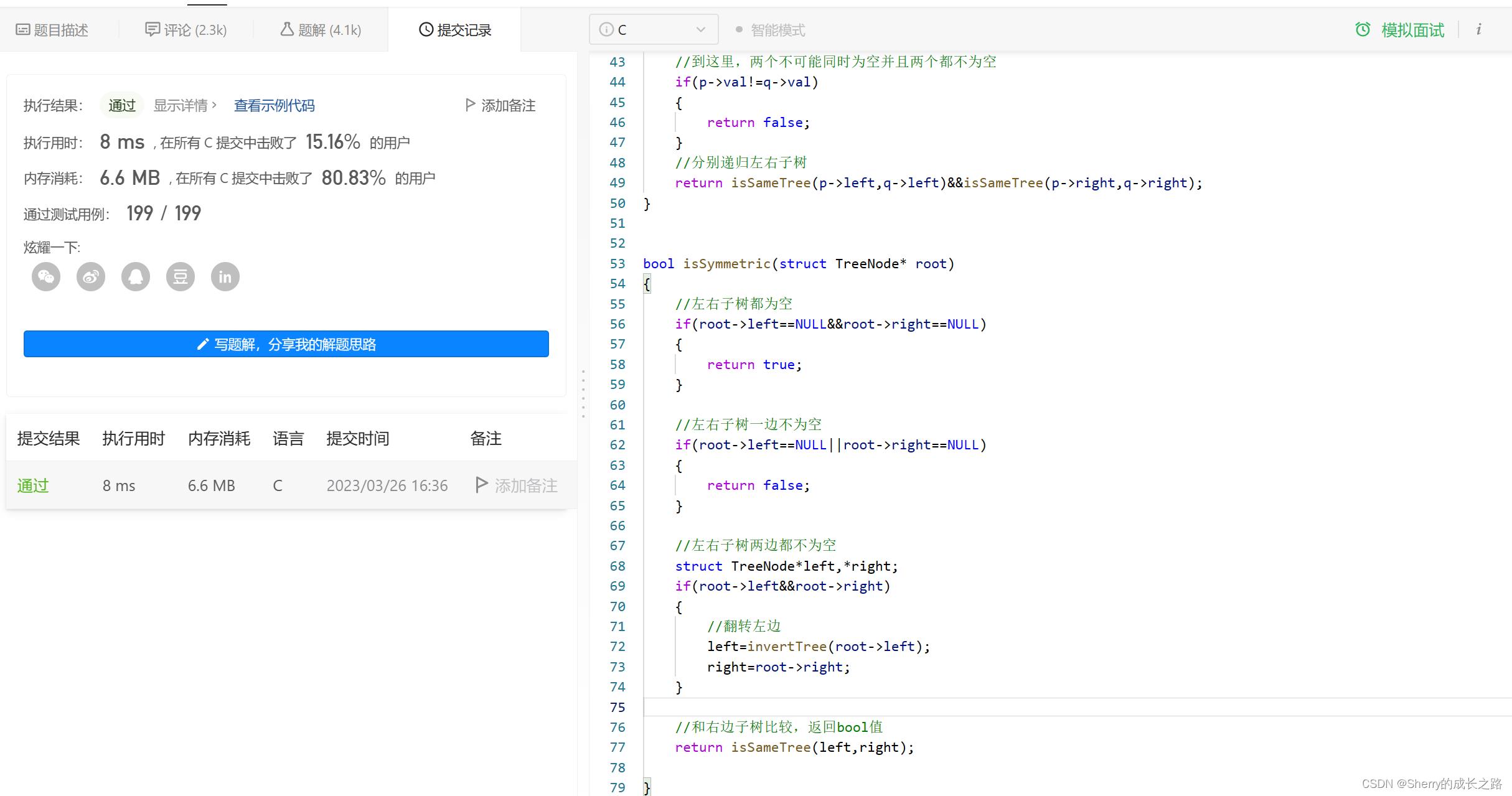
但是这种方法有一定缺陷，因为破坏了原本二叉树的结构，有更好的方法吗？

思路2：

一棵树对称就是 它的左右子树呈镜像状态。说白了就是节点左子树的值等于右子树的值，右子树的值等于左子树的值。

那么我们可以用一个 check 函数来递归检查，并将二叉树的根节点传两份过去

如果两棵树都为空，返回真；
如果两棵树一棵为空，另一棵不为空，返回假；
如果两棵树都不为空，但是值不相等，返回假；
上面都没有返回，那么分别递归第一棵树的左子树和第二棵树的右子树；第一棵树的右子树和第二棵树的左子树。
最后返回 check 函数的值，判断结果。

bool check(struct TreeNode* p,struct TreeNode* q)
 
     if(p==NULL&&q==NULL)
     
         return true;
     

     if(p==NULL||q==NULL)
     
         return false;
     

     if(p->val!=q->val)
     
         return false;
     
    //递归
     return check(p->left,q->right)&&check(p->right,q->left);
 


bool isSymmetric(struct TreeNode* root)

   
    return check(root,root);

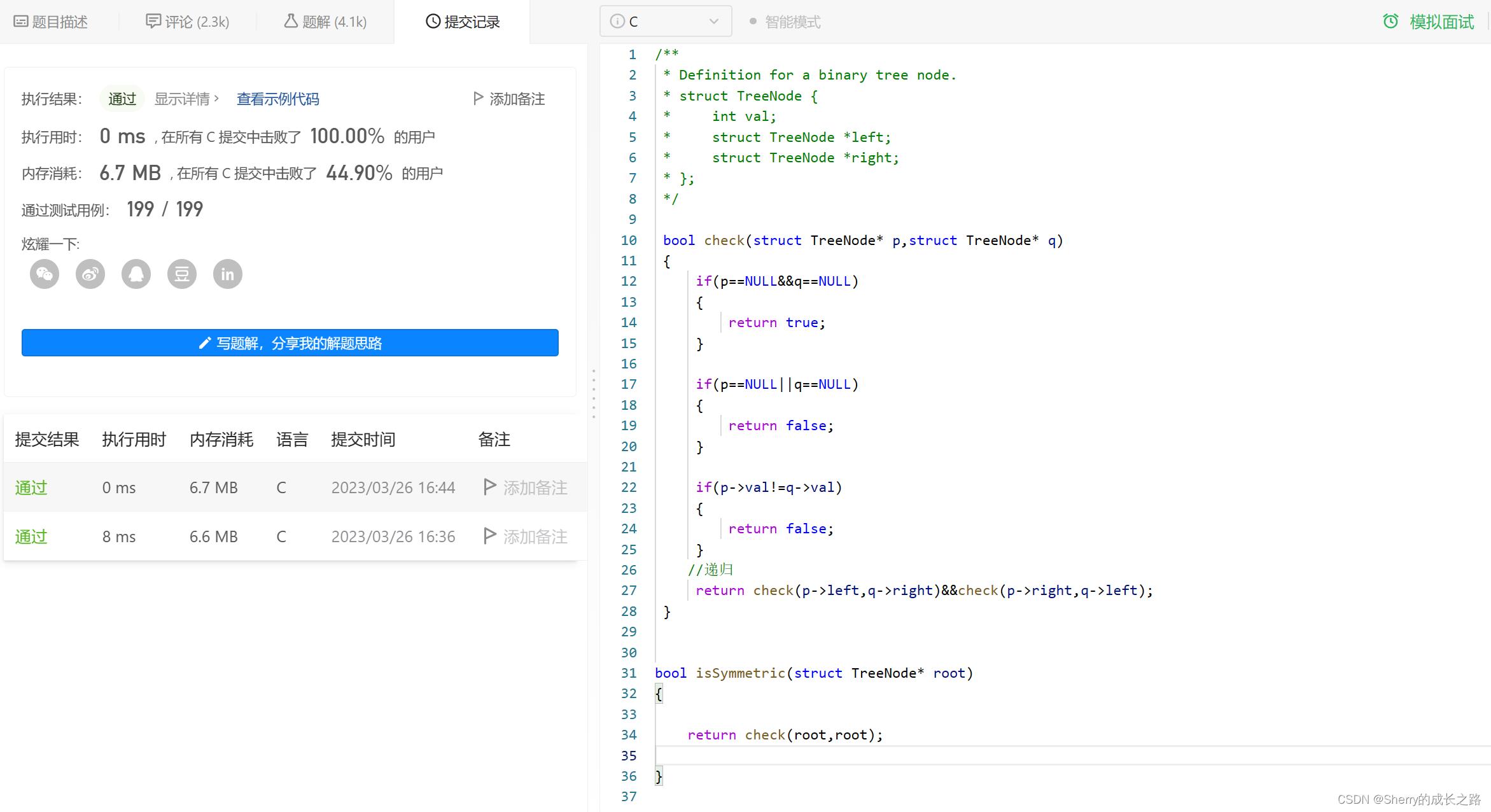
总结：

今天我们分析并完成二叉树OJ题(一)，通过分析明白了原理，愿这篇博客能帮助大家理解这些OJ题，因为二叉树相关OJ题是还是有一些难度和细节需要注意。下一篇博客将继续完成一些二叉树OJ题。希望我的文章和讲解能对大家的学习提供一些帮助。

当然，本文仍有许多不足之处，欢迎各位小伙伴们随时私信交流、批评指正！我们下期见~

数据结构之二叉树基础OJ练习单值二叉树

单值二叉树

题目来源：

单值二叉树

题目描述：

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 1：

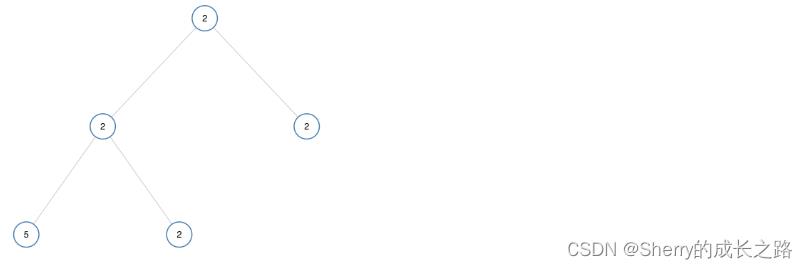
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

输入：[2,2,2,5,2]
输出：false

解题思路：

==具有传递性，比如：a==b && a==c，b==e && b==f，可以得到a==b==c==e==f

该题的思路是比较一个父亲和左右孩子的值是否相等，然后进行递归再判断左子树右子树是不是单值二叉树

代码如下：

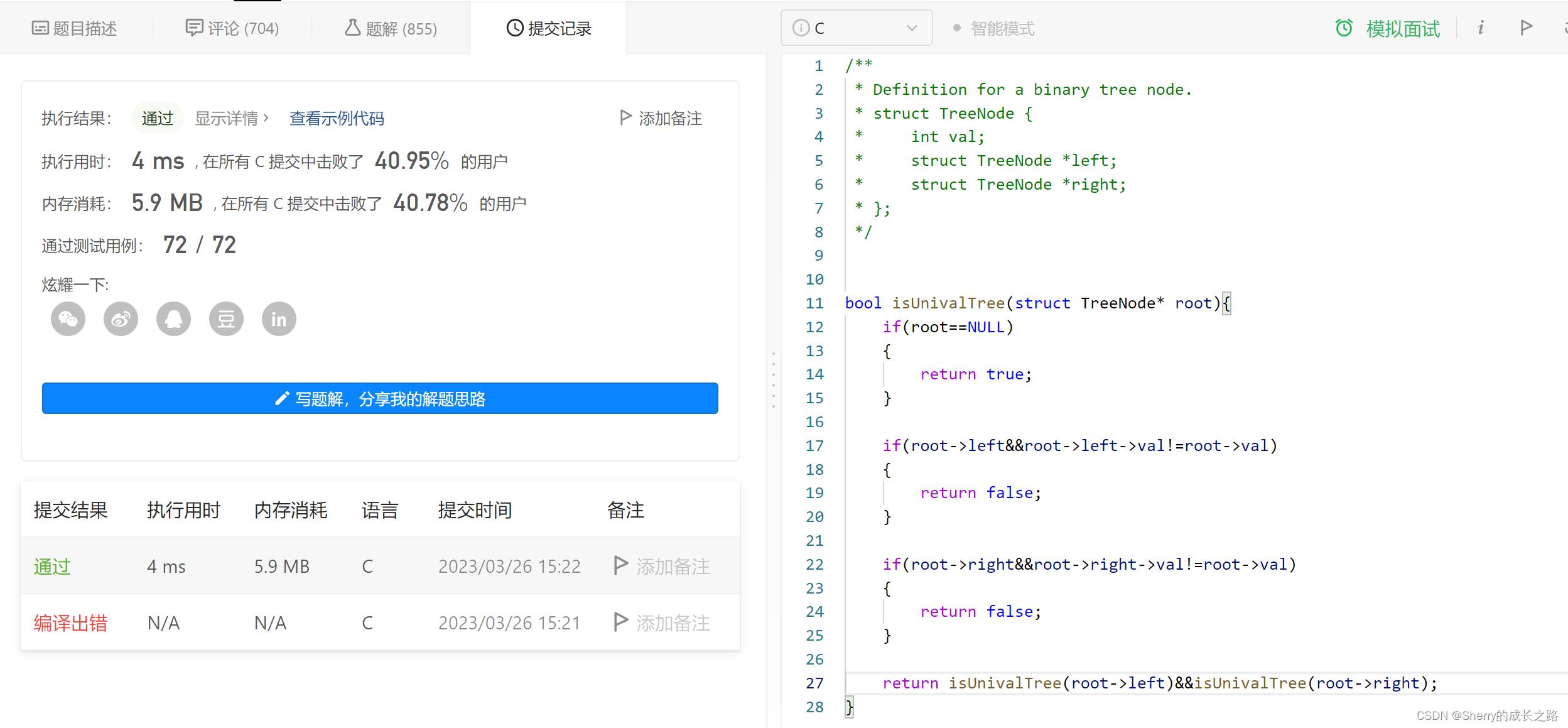
bool isUnivalTree(struct TreeNode* root)
{
    if(root==NULL)//root为空时，返回true
    {
        return true;
    }
    //父亲和左右孩子比
    if(root->left && root->left->val != root->val)//左孩子存在并且左孩子的值不等于父亲的值，返回false
        return false;
 
    if(root->right && root->right->val != root->val)//右孩子存在并且右孩子的值不等于父亲的值，返回false
        return false;
    
    return isUnivalTree(root->left) && isUnivalTree(root->right);//判断左子树和右子树是不是单值二叉树
}

以上是关于创作赢红包＜ 二叉树OJ题 ＞单值二叉树&&二叉树的最大深度&&翻转二叉树&&相同的树&&对称二叉树的主要内容，如果未能解决你的问题，请参考以下文章

数据结构之二叉树基础OJ练习单值二叉树

数据结构学习笔记（二叉树）OJ题总结与整理

数据结构学习笔记（二叉树）OJ题总结与整理

单值二叉树（2021-8-8）

数据结构二叉树经典基础习题

2021-10-22刷题总结