MATLAB | 三个趣的圆相关的数理性质可视化

Posted 2022-09-20 slandarer

椭圆的准圆

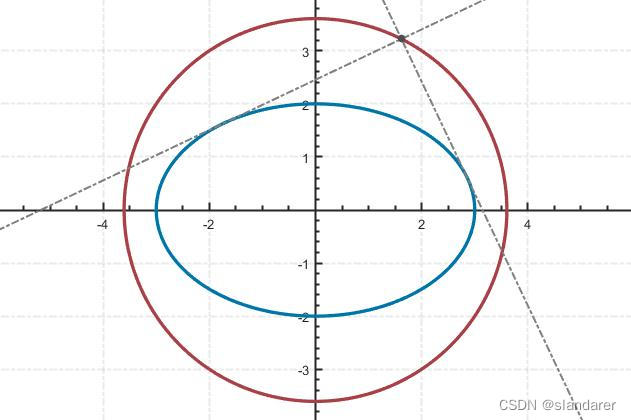
命题1: 椭圆外一点向椭圆做两条切线，若两切线垂直，则点的轨迹为圆形。

简单说明下为啥：
对于椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,假设其过$(m,n)$点的切线方程为$y-n=k(x-m)$，带入得椭圆方程得：

$$\begin{array}{rl}& b^2{x}^2+a^2(k^2(x-m{)}^2+2nk(x-m)+n^2)-x^2{b}^2=0\\ & (a^2{k}^2+b^2)x^2+2k{a}^2(n-mk)x+a^2(km-n{)}^2-a^2{b}^2=0\end{array}$$

由于求的是切线因而$\Delta =0$,即$(m^2-a^2)k^2-2mnk+n^2-b^2$,这是一个关于$k$的约束条件，由伟达定理得到两条切线的斜率$k_1,k_2$满足条件：
$$k_1{k}_2=\frac{n^2-b^2}{m^2-a^2}$$
由于两切线垂直，因此$k_1{k}_2=-1$，因而有:
$$m^2+n^2=a^2+b^2$$
是一个半径为$\sqrt{a^2+b^2}$的圆。

可视化效果：

MATLAB代码:

function directorC
% @author : slandarer
% 公众号  : slandarer随笔
% 知乎    : hikari
a=3;b=2;syms k
% axes基础属性设置
ax=gca;
hold on;grid on
ax.XLim=[-6,6];
ax.YLim=[-4,4];
ax.DataAspectRatio=[1,1,1];
ax.XAxisLocation='origin';
ax.YAxisLocation='origin';
ax.LineWidth=1.5;
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.GridLineStyle='-.';
ax.GridAlpha=.09;
% 绘制圆和椭圆
t=linspace(0,2*pi,200);
plot(a.*cos(t),b.*sin(t),'LineWidth',2.5,'Color',[0,118,168]./255)
plot(sqrt(a^2+b^2).*cos(t),sqrt(a^2+b^2).*sin(t),'LineWidth',2.5,'Color',[169,64,71]./255)
% 绘制切线和交点
thetaList=linspace(0,2*pi,200);
kline1=plot(0,0,'-.','LineWidth',1.5,'Color',[1,1,1].*.5);
kline2=plot(0,0,'-.','LineWidth',1.5,'Color',[1,1,1].*.5);
kpnt=scatter(a,0,'filled','CData',[1,1,1].*.3);
X=-6:.1:6;
% 循环绘图
for i=1:length(thetaList)
    theta=thetaList(i);
    m=sqrt(a^2+b^2).*cos(theta);
    n=sqrt(a^2+b^2).*sin(theta);
    kk=double(solve((m^2-a^2)*k^2-2*m*n*k+n^2-b^2==0)); 
    Y1=kk(1).*(X-m)+n;Y2=kk(2).*(X-m)+n;
    kline1.XData=X;kline1.YData=Y1;
    kline2.XData=X;kline2.YData=Y2;
    kpnt.XData=m;
    kpnt.YData=n;
    drawnow;
    pause(.01)
end
end

旋转的错觉

命题2: 假设有半径为$\frac{r}{2}$的小圆在半径为$r$大圆内滚动，小圆上的点轨迹为直线。

证明很简单，假设此时小圆上有一点与大圆接触，且此时小圆圆心与原点的连线与x轴正方向的夹角为${\theta }_0$，现假设小圆滚动导致小圆圆心夹角变化$\theta$，由于小圆半径为大圆的一半，因而当滚过相同路程时，小圆上的点的夹角反方向变化$2\theta$因而可以求出该小圆上点位置变化参数方程：

x