临界频带和听觉滤波器

Posted 2023-04-01 cucjing

一 实验目的

1、线性频率—听觉心理尺度的转换：将频谱展示的线性频率横轴，转换为Bark尺度值、ERB尺度值、倍频程序号、1/3倍频程序号；

2、频带划分：将0~fs/2的频率范围，划分成一组基于Bark或ERB的感知频带。以整数尺度为中心频率，以对应的Bark或ERB带宽为频带宽度。给出对应的频谱展示。

二 实验原理

1、临界带率尺度（CB Rate Scale）

500Hz以下，临界带宽100Hz左右。之后临界带宽随着频率增加而增大，与0.2f虚线作对比，开始临界带宽增大慢一些，3kHz以后临界带宽增大变得更快。近似表述：即500Hz以下为常量100Hz，500Hz以上则为中心频率的20%。

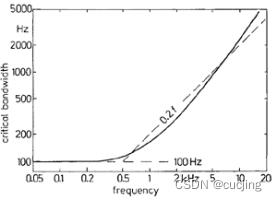
图2.1 临界带宽随频率变化的曲线图

量化模型：Zwicker和Terhard在1980年提出临界带宽数学表达式：

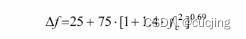
fc是中心频率，以KHz为单位。∆f是对应该中心频率的临界带宽，单位为Hz。以1KHz中心频率为例，经过上式计算，可以得到对应临界带宽是162Hz。

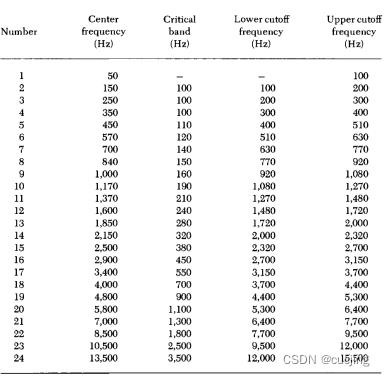
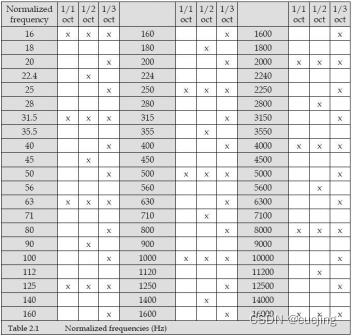
表2.1给出完整临界带参数，包括单个临界带上限和下限以及带宽。共有25个临界带（有的是24个）。前一临界带上限频率即后一临界带下限频率。

表2.1 常用临界带配置

2、Bark尺度

图2.2展示了临界带序号和频率之间的对应关系。纵坐标为可听频率区域划分为24个相邻临界带，产生一个临界带率尺度—Bark 尺度。

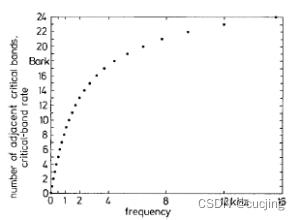
图2.2  Bark尺度与频率尺度的关系曲线

Terhard和Zwicker提出bark尺度和频率之间的转换关系公式：

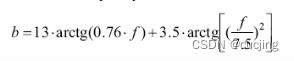
1997年Tsoukalas提出简化的关系公式：

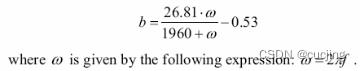
3、等效矩形带宽（Equivalent Rectangular Bandwidth，ERB）

1983年Glasberg和Moore提出ERB，用于从滤波器中心频率计算等效临界带宽。所谓等效，是指和滤波器所通过的能量相同。一般是设计矩形滤波器，高度和听觉滤波器顶点一样，宽度比3dB带宽稍大，保证通过能量相等，如下图：

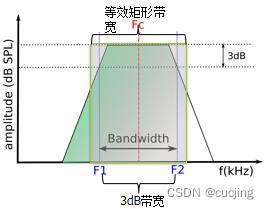
图2.3 矩形滤波器

  

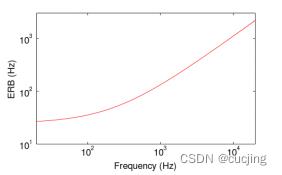
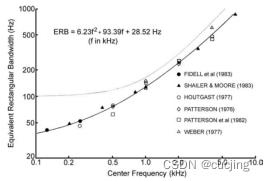
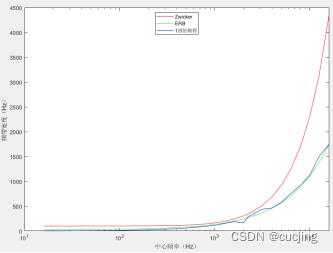
图2.4 ERB带宽和中心频率关系曲线

图2.4左图为ERB带宽和中心频率关系。近似线性公式为：

B=24.7×[(4.37×f_c)+1]Hz

右图是基于多个测量数据拟合的ERB带宽和线性频率的关系曲线，以及与传统Bark临界频带（点线）的对比，频率单位kHz，适用于中心频率100Hz—10kHz之间的情况。更一般的公式为：

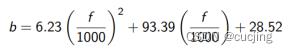
ERB尺度和线性频率之间的转换：

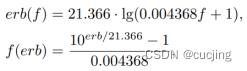
对于数字音频96kHz采样率，其奈奎斯特频率48kHz，对应ERB尺度是40。通常ERB尺度取值在1~40之间。设计滤波器组时，经常用ERB尺度作为频带划分标准，中心频率取ERB尺度的1到40整数值等间隔。

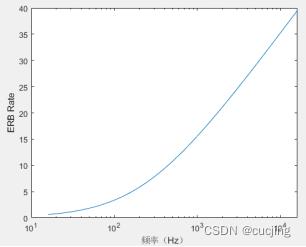
图2.5 ERB尺度和线性频率的关系

4、其他频带划分方法：倍频程和1/3倍频程

1/3倍频程和ERB临界带宽分布接近，所以广泛应用于声学测量和分析领域。

新旧临界带宽计算方法，以及1/3倍频程带宽的对比。中心频率选择表中1/3倍频程的中心频率点。

三、实验程序

1、Bark尺度-频率转换公式：

clear;
clc;
clf;
%Bark尺度值
f=0:1.6*10^4;
Bark_1=13.*atan(0.76*f/1000)+3.5*atan(f.^2 /((7500)^2));
Bark_2=26.81./(1+(1960./f))-0.53;
figure(1);
plot(f,Bark_1);hold on;plot(f,Bark_2);
xlabel('Hz');ylabel('Hz'); grid on;
legend('Bark1','Bark2');
title('Bark Scale');
%ERB尺度值
ERB_1=(24.7*((4.37*f/1000)+1));
ERB_2=6.23*(f.^2/((1000)^2))+93.39*f/1000+28.52; 
ERB_3=21.366*log(0.004368*f+1);
figure(2);
subplot(2,1,1);
plot(f, ERB_1);hold on;plot(f,ERB_2);
xlabel('Hz');ylabel('Hz'); grid on;
legend('ERB_1','ERB_2');
title('ERB Scale');
subplot(2,1,2);
plot(f, ERB_3);
xlabel('Hz');ylabel('Rate'); grid on;
Fs=[50 150 250 350 450 570 700 840 1000 1170 1370 1600 1850 2150 2500 2900 3400 4000 4800 5800 7000 8500 10500 13500];
Band=[100 100 100 100 110 120 140 150 160 190 210 240 280 320 380 450 550 700 900 1100 1300 1800 2500 3500];
figure(3);
bar(Fs,Band);grid on;
title('Bark Frequency Spectrum');

2、频带划分成一组基于Bark的感知频带：

clear;
clc;
clf;
% 三分之一倍频
%F1=@(t)25+75*((1+1.4*t.^2).^0.69);
F1=@(t)6.23*(t.^2/((1000)^2))+93.39*t/1000+28.52
sf=256;
n=16000;
t=0:1:n;
x=F1(t);
f = [16.0 20.0 25.0 31.5 40.0 50.0 63.0 80.0 100.0 125.0 160.0];
fc = [f,10*f,100*f];
oc6 =2^(1/6); %中心频率与下限频率的比值
nc =length(fc); %取中心频率总的长度 
nfft = 2^nextpow2(n); % 大于并最接近n的2的幂次方长度
a =fft(x,nfft); % FFT变换
yc = zeros(1,nc);
for j =1:nc 
    fl = fc(j)/oc6; %下限频率 
    fu =fc(j)*oc6; % 上限频率
    nl = round(fl*nfft/sf+1); % 下限频率对应的序号
    nu = round(fu*nfft/sf+1); % 上限频率对应的序号
    if fu >sf/2 % 如果上限频率大于折叠频率则循环中断
        m = j-1; 
        break
    end
    %以每个中心频率段为通带进行带通频域滤波 
    b = zeros(1,nfft);
    b(nl:nu) = a(nl:nu);
    b(nfft-nu+1:nfft-nl+1) = a(nfft-nu+1:nfft-nl+1);
    c = ifft(b,nfft);
    %计算对应每个中心频率段的有效值
    yc(j) = sqrt(var(real(b(1:n))));
end
%绘制输入时程曲线
subplot(2,1,1);plot(t,x);
xlabel('Hz');ylabel('Hz');grid on; 
%绘制三分之一倍频程有效值图形
subplot(2,1,2); plot(fc(1:m),yc(1:m));
xlabel('Hz');ylabel('Hz'); grid on;

四、实验结果

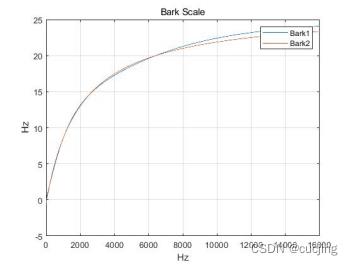
图4.1 Bark尺度值

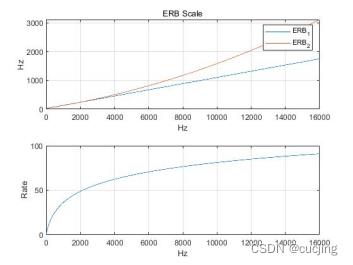
图4.2 ERB尺度值

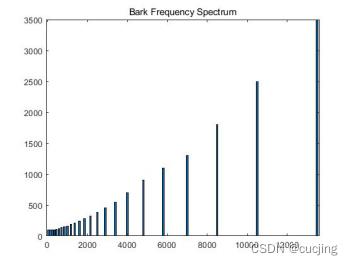
图4.3 Bark频带划分

五、结果分析

物理上的频率尺度并不非常适合用来描述内耳的听觉特性。早期临界带宽计算缺陷，低频数据很少，对临界带的估计方法不够精确。沿着基底膜的方向，Bark尺度看起来应该是最适合描述听觉系统频率选择特性的尺度。临界带率尺度和其他几个描述听觉系统特征的尺度有很强的线性相关性。

评语：对题目理解有误。作业要求的是在频谱展示时，把横轴的线性频率，替换成Bark或者ERB等尺度，而不是直接展示Bark和线性频率之间的关系。你得给出一段声音的频谱，然后把横坐标换掉。第二题中关于1/3倍频程的那段代码，是不需要做滤波的，你只需要计算每个1/3倍频带范围内的能量值之和，也就是把nl到nu的fft的绝对值求平方和即可。b这个参量没有必要，也不用ifft。最后就是要用实际音频来做。

实时音频编解码之八 频带扩展

本文谢绝任何形式转载，谢谢。

1.4.8 频带扩展

在线性预测应用中，由于极点过于靠近单位圆，合成滤波器可能处于临界稳定的状态，在定点实现中这一问题更加严重，定点的量化和计算中的精度损失可能使得临界稳定的滤波器变得不稳定（极点位于单位圆外），这会导致合成的信号偶尔有杂音。可以通过调节LPC系数改善滤波器稳定性：
$$a_{ne{w}_i}={\gamma }^i{a}_i;i=1,2,\cdots ,M$$
其中$0<\gamma <1$，$\gamma$为常量，常取0.988到0.996范围内的值，该运算使得合成滤波器的所有极点向原点迅速靠拢，这提升了滤波器的稳定性。这使得谱峰变平坦，宽度变宽。频带扩展的另一个好处是缩短了脉冲响应的持续时间，这提升了信道的鲁棒性，这是因为由信道引入的激励信号失真会被合成滤波器过滤掉一部分，短的脉冲响应缩短了信道误差的影响。