BulletproofsSigma protocolHalo2等ZK方案小结

Posted 2022-09-09 mutourend

1. 引言

当前的ZK构建方案有：

• 1）Bulletproofs
• 2）Sigma protocol（+ Fiat-Shamir）
• 3）Halo2
• 4）Plonky2
• 5）MPC-in-the-head proof（MPCith）

2. Bulletproofs

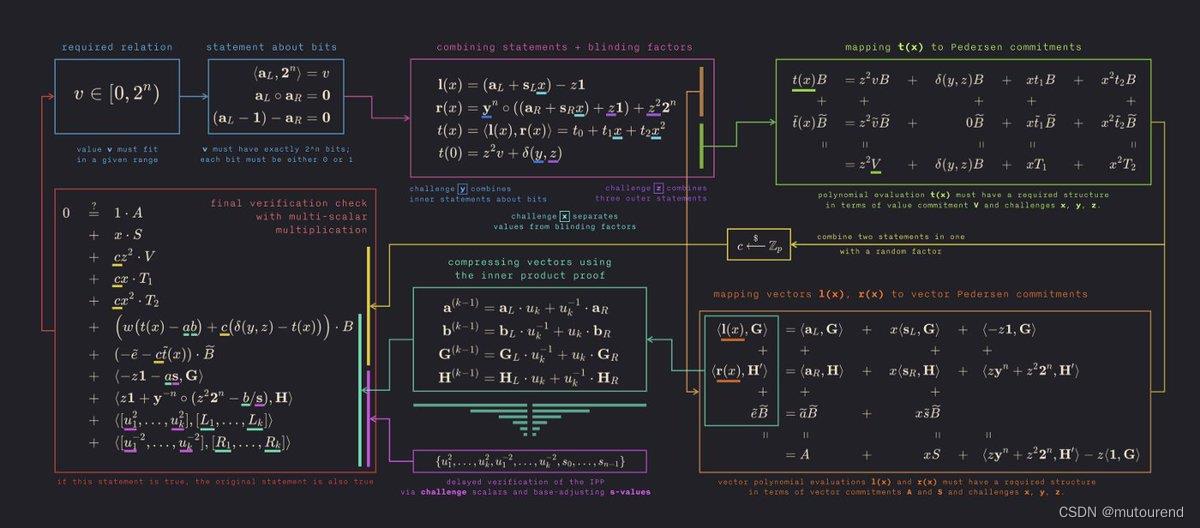
Bulletproofs的特点为：

• 1）无需trusted setup的short NIZK
• 2）基于Pedersen commitment构建
• 3）支持proof aggregation
• 4）Prover time为：$O(N\cdot \log (N))$，约30秒
• 5）Verifier time为：$O(N)$，约1秒
• 6）proof size为：$O(\log (N))$，约1.3KB
• 7）基于的安全假设为：discrete log

Bulletproofs适用的场景为：

• 1）range proofs（仅需约600字节）
• 2）inner product proofs
• 3）MPC协议中的intermediary checks
• 4）aggregated and distributed (with many private inputs) proofs

Bulletproofs不适合的场景有：

• 1）需在链上验证的复杂任意statement

目前Bulletproofs方案已用于：

• 1）比特币的隐私交易：ELEMENTS Confidential Transactions
• 2）Monero：Monero Becomes Bulletproof
• 3）Stellar Shielded Tx（Cloak）：Cloak隐私资产协议

当前Bulletproofs开源库有：

• 1）https://github.com/dalek-cryptography/bulletproofs（Rust）
• 2）https://github.com/adjoint-io/bulletproofs（Haskell）
• 3）https://github.com/bbuenz/BulletProofLib（Java）

Bulletproofs相关学习资源有：

• 1）Stanford Bulletproofs
• 2）论文作者Benedikt Bünz Bulletproofs视频
• 3）Building on Bulletproofs

3. Sigma Protocol（+ Fiat-Shamir）

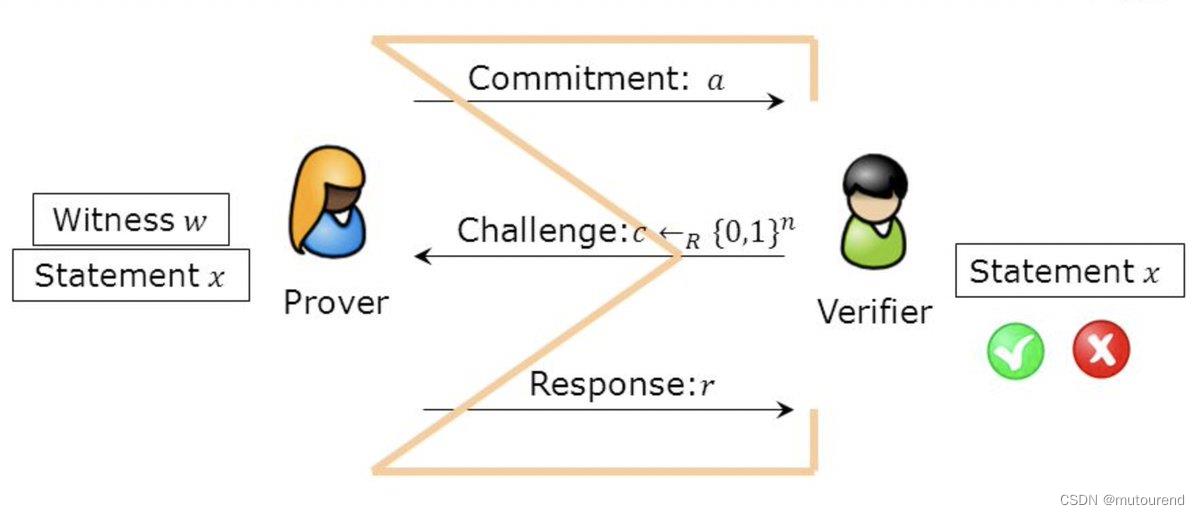
Sigma Protocol（+ Fiat-Shamir）特点为：

• 1）无需trusted setup的short proof。
• 2）需要constant number（3）of public-key operations。
• 3）可配置组合多个Sigma proofs，类似为A and\\or B、eq(A,B)、all(n,A)。
• 4）基于的安全假设为：discrete log，honest verifier。

Sigma Protocol（+ Fiat-Shamir）适于的场景为：

• 1）discrete log（dlog）proofs
• 2）one-of-many dlogs
• 3）discrete log equality（dleq）

Sigma Protocol（+ Fiat-Shamir）不适合的场景有：

• 1）复杂任意计算。

当前Sigma Protocol已用于：

• 1）Signal (Algebraic MACs for group chats)：Technology Preview: Signal Private Group System
• 2）dleq proofs in the adaptor signatures
• 3）verifiable random functions
• 4）ElGamal encryption in the Cryptography for #MeToo

Sigma Protocol相关开源库有：

• 1）https://github.com/LLFourn/secp256kfun/tree/master/sigma_fun（Rust）
• 2）https://pkg.go.dev/go.dedis.ch/kyber/v4/proof（Go）
• 3）https://github.com/cryptobiu/libscapi（C++）
• 4）https://github.com/spring-epfl/zksk（Python）

Sigma Protocol相关学习资料有：

• 1）Zero Knowledge Proofs with Sigma Protocols
• 2）Sigma Protocols and (Non-Interactive) Zero Knowledge
• 3）ZKProof Standardizing Sigma Protocols?

4. Halo2

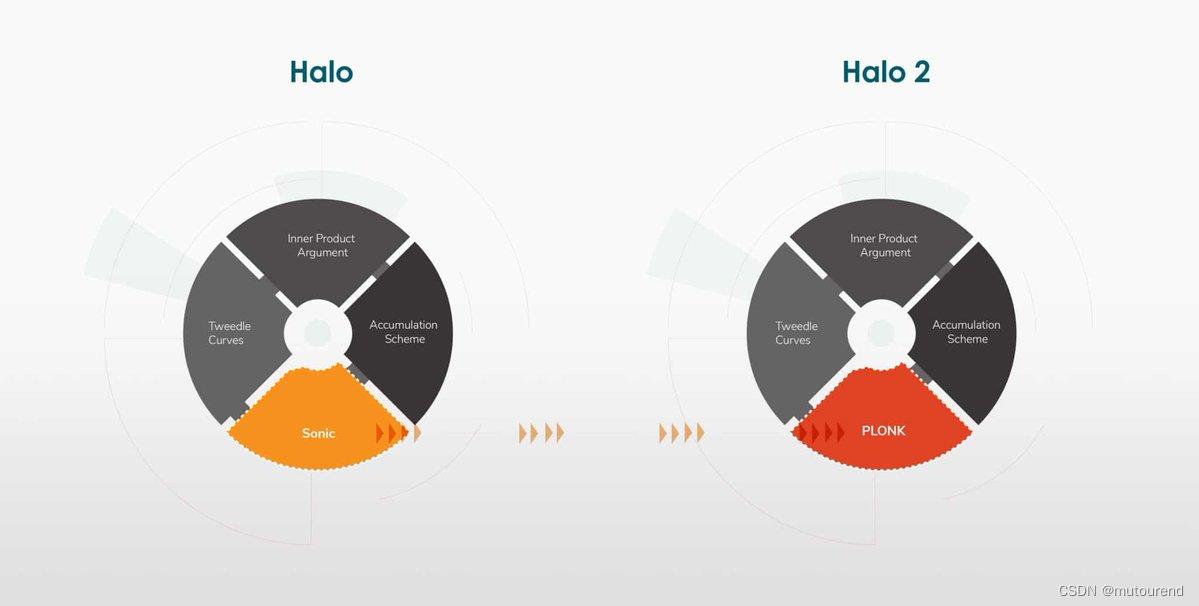
Halo2主要特点为：

• 1）无需trusted setup，将accumulation scheme 与 PLONKish arithmetization高效结合。
• 2）基于IPA commitment scheme。
• 3）繁荣的开发者生态。
• 4）Prover time为：$O(N\ast \log N)$。
• 5）Verifier time为：$O(1)>$Groth16。
• 6）Proof size为：$O(\log N)$。
• 7）基于的安全假设为：discrete log。

Halo2相关开源库有：

• 1）https://github.com/zcash/halo2：ZCash官方版本，采用IPA承诺机制。
• 2）https://github.com/privacy-scaling-explorations/halo2wrong：将ZCash官方版本中的IPA承诺机制替换为KZG承诺机制。
• 3）https://github.com/Orbis-Tertius/halo2：将ZCash官方版本中的IPA承诺机制替换为FRI承诺机制。（开发中）
• 4）Mina Kimchi proof system：Mina版本，Halo2部分见https://github.com/o1-labs/proof-systems（Rust），递归实现见https://github.com/MinaProtocol/mina/tree/develop/src/lib/pickles（OCaml）。

Halo2适于的场景有：

• 1）任意可验证计算
• 2）递归proof composition
• 3）基于lookup-based Sinsemilla function的circuit-optimized hashing

Halo2不适于的场景为：

• 1）除非替换使用KZG版本的Halo2，否则在以太坊上验证开销大。

当前ZCash官方版本暂未支持递归，目前递归可用的有：

• 1）Scroll团队KZG版本的https://github.com/scroll-tech/halo2-snark-aggregator
• 2）Orbis Labs团队正在使用Tiny-RAM架构构建其accumulation scheme：https://github.com/Orbis-Tertius/tiny-ram-halo2

目前Halo2已用于：

• 1）ZCash shielded protocol（Orchard）：Bringing Halo 2 to Zcash
• 2）Scroll zkEVM：Scroll zkEVM
• 3）Orbis ZK-Rollup on Cardano：https://github.com/Orbis-Tertius/Orbis
• 4）Dark Fi L1：Dark.fi

Halo2相关学习资料有：

• 1）基本解释：Explaining Halo 2
• 2）doc：Halo2文档
• 3）视频：Zcash: Halo 2 and SNARKs without Trusted Setups
• 4）数学：2021年11月Vitalik博客Halo and more: exploring incremental verification and SNARKs without pairings
• 5）Halo2生态展示：2022年8月视频Halo 2 Community Showcase - Ying Tong at Zcon3
• 6）更多：https://github.com/adria0/awesome-halo2

5. Plonky2

Plonky2主要特点为：

• 1）无需trusted setup，将FRI与PLONK结合。
• 2）针对具有SIMD的处理器进行了优化，并采用了64 byte Goldilocks fields。
• 3）Prover time为：$O(\log N)$。
• 4）Verifier time为：$O(\log N)$。
• 5）Proof size为：$O(N\ast \log N)$。
• 6）基于的安全假设为：collision-resistant hash function。

Plonky2的主要特色在于：

• 1）支持如下选择：
  • 1.1）选择fewer rows，意味着fast prover；
  • 1.2）选择fewer columns，意味着fast verifier。
• 2）根据https://github.com/Sladuca/sha256-prover-comparison中的对比可知：
  • 2.1）Plonky2 STARK is ~38x faster than Halo2, ~64x faster than Groth16 on 3yo MBP。
  • 2.2）Plonky2 STARK does 142 hashes/sec on a 2021 MBP with an M1 processor。
• 3）FRI中使用Poseidon sponge和GMIMC作为哈希函数。

Plonky2适于的场景有：

• 1）任意可验证计算。
• 2）递归proof composition。
• 3）使用自定义gate进行电路优化。

Plonky2不适于的场景为：

• 1）受限于其non-native arithmetic，不适于包含椭圆曲线运算的statements。

Plonky2已用于：

• 1）Polygon Zero（ZK L2，早期名为Mir protocol）

Plonky2相关开源库见：

• 1）https://github.com/mir-protocol/plonky2

Plonky2相关学习资料见：

• 1）Introducing Plonky2
• 2）Plonky2论文 Plonky2: Fast Recursive Arguments with PLONK and FRI

6. MPC-in-the-head proof

相关论文有：

• 2021年论文 Formal security analysis of MPC-in-the-head zero-knowledge protocols：开源代码见：https://github.com/Nsidorenco/Decomposition-zk。形式化安全分析，采用eC语言。

所谓MPC是指：

• 1）各方可基于其私有输入进行分布式计算。
• 2）每方都生成一个transcript（its view）。
• 3）关键点在于#1：若MPC的最终结果出错，则在某处存在inconsistent view。

所谓Secret Sharing秘密共享：

• 1）为MPC的一种常用抽象，将某个秘密切分给多方，使得他们需共同协作来使用该秘密。
• 2）关键点在于#2：若仅公开共享的部分秘密，则该秘密仍是未知的。

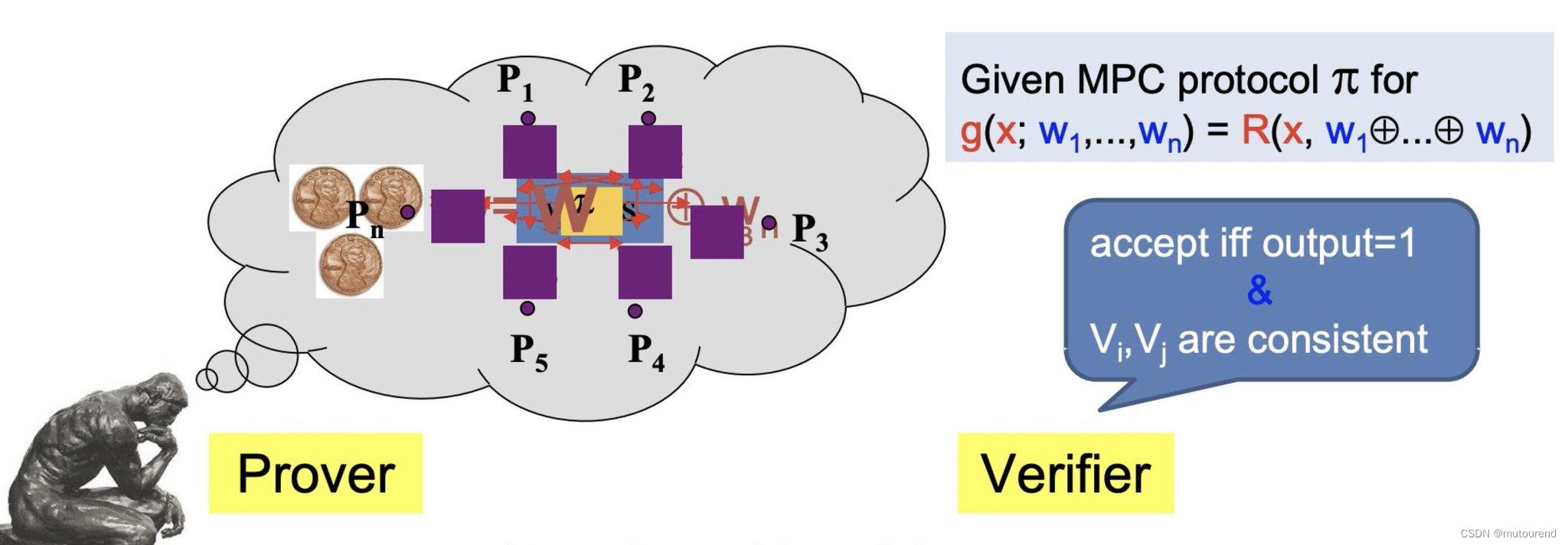
所谓MPC-in-the-head（MPCith）是一个ZK系统：

• 1）Prover会simulate an MPC "in their head"来基于 某private input（已分享给多个虚拟方） 计算任意函数。注意，所simulate的各方会根据其所使用的秘密块来生成a view。
• 2）Verifier会请求公开这些view的一个子集，公开的子集数量不足以恢复出该private input，但是又能从信任发生不一致性的概率很低。若概率不够低，可重复这种交互多次（如约300次）。
• 3）可使用Fiat-Shamir将以上过程实现为非交互式的，并可并行化。
• 4）生成proof所用的底层MPC原语并不重要，仅所生成的views是重要的。从而可将simulated MPC看成是黑盒略过，从而可避免大量开销。

MPCith：

• 1）用于boolean circuits效率很高，不像大多数其它NIZKs仅适于arithmetic circuit。
• 2）可与具有private addresses的RAM进行扩展。从而很容易将verifiable computation circuit编译为任意程序。

MPCith的特点为：

• Prover time为：$O(N)$< Groth16。
• Verifier time为：$O(N)$。
• Proof size为：$O(N)$。
• 加法运算是free的，乘法运算占用大多数开销。
• 进行可验证计算的开销要低很多：为（1/n_reps*n_parties=> 约1/600），要远低于SNARKs的（约1/100万）。

MPCith适于的场景有：

• 1）boolean circuit：
  • 1.1）对于不易于转换为arithmetic circuit的复杂程序，如SHA hashes；
  • 1.2）机器学习以及设计浮点运算的近似计算，可借助boolean circuit实现逐位运算。
• 2）delegated proving（证明委托）：
  • 2.1）如需为某statement创建SNARK，但不想自己计算，也不想将witness告知第三方的情况。可创建一个MPCith proof，然后委托方可创建一个新的证明来验证该MPCith proof。

MPCith不适于的场景为：

• 1）任何需要进行链上验证的场景。

目前MPCith已用于：

• 1）微软PICNIC（抗量子签名方案）：https://github.com/microsoft/Picnic

MPCith相关开源库有：

• 1）https://github.com/trailofbits/reverie/tree/stacked-ikos（Rust）：Reverie is an implementation (prover and verifier) of the MPC-in-the-head NIZKPoK。
• 2）https://github.com/cronokirby/boo-hoo（Rust）：ZKBoo。
• 3）https://github.com/cronokirby/Rem-Boo（Rust）：Fast ZK proofs over boolean circuits with RAM。

MPCith相关学习资料有：

• 1）2022年8月6日episode：MPC In The Head Special
• 2）入门论文：2016年 ZKBoo: Faster Zero-Knowledge for Boolean Circuits
• 3）安全分析：2021年论文 Formal security analysis of MPC-in-the-head zero-knowledge protocols：开源代码见：https://github.com/Nsidorenco/Decomposition-zk。形式化安全分析，采用eC语言。

参考资料

[1] twitter ZK方案之Bulletproofs、Halo2小结
[2] twitter MPC-in-the-head proofs