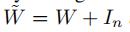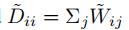GCN笔记：Graph Convolution Neural Network，ChebNet

Posted 2022-09-05 UQI-LIUWJ

在 GNN笔记：图卷积_UQI-LIUWJ的博客-CSDN博客中，我们知道了谱图卷积相当于是

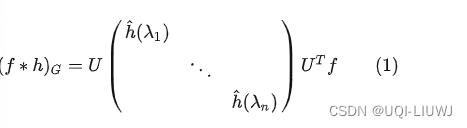
那么问题在于，如何设计含有可训练的、共享参数的kernel呢？ 

1 GCN-ver1.0 （2013）

1.0 原理

Spectral Networks and Deep Locally Connected Networks on Graphs

• 谱图卷积核
• 这里就是可学习的参数

1.1 弊端

• 每一次前向传播，都需要计算和,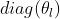和U三者的矩阵乘积
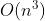
  • ——>计算复杂度高 
• 卷积核需要n个参数
• 不具有spatial localization（即不能很好地体现 k-阶邻居的这个信息）

2 ChebNet

2.1 原理

• 使用切比雪夫多项式作为谱图卷积的卷积核
  • 
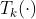  • ——k阶切比雪夫多项式
  • βk——对应的系数（训练中迭代更新的参数）
  • 
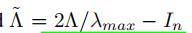
    • λmax表示拉普拉斯矩阵L最大的特征值 
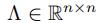    •  是L的特征值组成的对角矩阵
• ——>
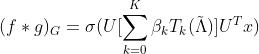
• 进一步推导（把矩阵运算放到切比雪夫多项式里面），有
  • 
  • ——>
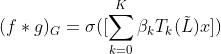
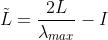
    • 其中        
  • 这样变换的好处是：计算过程中无需对拉普拉斯矩阵进行特征分解

2.1.1 为什么要限制?

 第一类切比雪夫多项式的解析形式是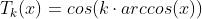

由于有arccos(x)函数，所以输入必须在[-1,1]之间

拉普拉斯矩阵半正定

——>拉普拉斯矩阵的特征值非负

——>

——>

——>

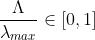
2.1.2 切比雪夫多项式

 2.2 K的含义

即图卷积的感受野

 

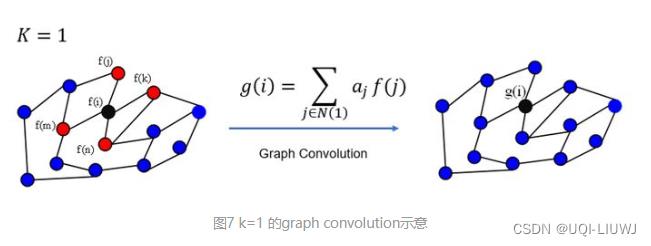
 注：实际的ChebNet 中，每一次卷积是把图中的所有顶点都做了一次上述的邻居点message passing

2.3 好处

• 卷积核只有K个参数（一般K远小于n，这样参数的数量级大大降低了）
• 矩阵变换后，不用再做特征分解了（λmax可以用幂迭代法得出）

   

  • ——>直接用拉普拉斯矩阵L进行计算 
  • 但由于要计算L^j,所以计算复杂度还是

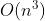
• 具有很好的spatial localization

  • K是卷积核的感受野

3 GCN_ver2.0（ChebNet的一阶近似）

• 一个层线性方程可以由堆叠多个使用拉普拉斯矩阵的一阶近似的局部图卷积层来达到相同的效果
  • （用深度换广度）
• 对ChebNet进行一阶近似，即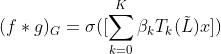中的K=1
• 同时， 由于在神经网络中，参数可以放大缩小，可以归一化，所以我们可以进一步假定

   

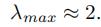
  •   因此，我们可以进一步将谱图卷积简化 （相当于上面切比雪夫多项式近似的时候，K取1，也就是只考虑1阶邻居）
  • 
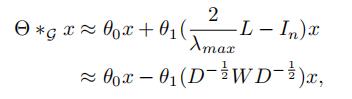
•  是谱图卷积核公用的参数。为了约束参数并为了稳定数值计算 ，θ0和θ1被一个参数θ代替：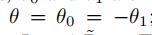

•    我们再令

  • 

    

  那么我们有：

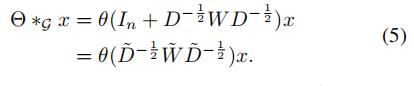
 堆叠K个一阶近似的图卷积可以获得和平行的K阶卷积相同的效果，所有的卷积可以从一个顶点的K阶邻居中获取到信息。