基于 LTspice 研究几种电路的频率特性
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于 LTspice 研究几种电路的频率特性相关的知识,希望对你有一定的参考价值。
§01 频率特性
一、RC无源
下面是单级 RC 低通滤波器电路图。使用 LTspice 研究其小信号 AC 频率特性。
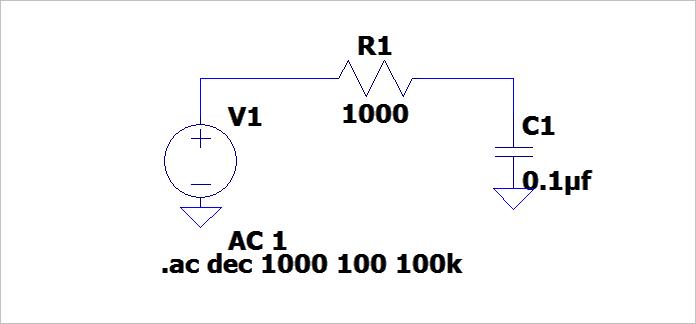
▲ 图1.1.1 测试单级RC低通滤波器
1、输出结果格式
交流分析输出的结果包括两部分,一个是增益部分,使用dB为单位。另一部分则是角度,单位是°。在存储的时候,需要将这两个部分进行分别进行存储,并绘制在幅值与角度部分。
| Freq. | V(n002) | I(C1) |
|---|---|---|
| 1.00000000000000e+002 | (-1.71115043445809e-002dB,-3.59527377986817e+000? | (-8.40535141371823e+001dB,8.64047262201318e+001? |
| 2.00000000000000e+002 | (-6.80451754744641e-002dB,-7.16245580672582e+000? | (-7.80838478950325e+001dB,8.28375441932742e+001? |
| 3.00000000000000e+002 | (-1.51629267198155e-001dB,-1.06747494123688e+001? | (-7.46456068056426e+001dB,7.93252505876312e+001? |
| 4.00000000000000e+002 | (-2.66008621896754e-001dB,-1.41078023715901e+001? | (-7.22612114281752e+001dB,7.58921976284099e+001? |
改造 LTS 程序,使他能够正确反映角度变化特性。
2、仿真结果
下面显示了 C1 上的电压与电流数值的变化与相位的变化。
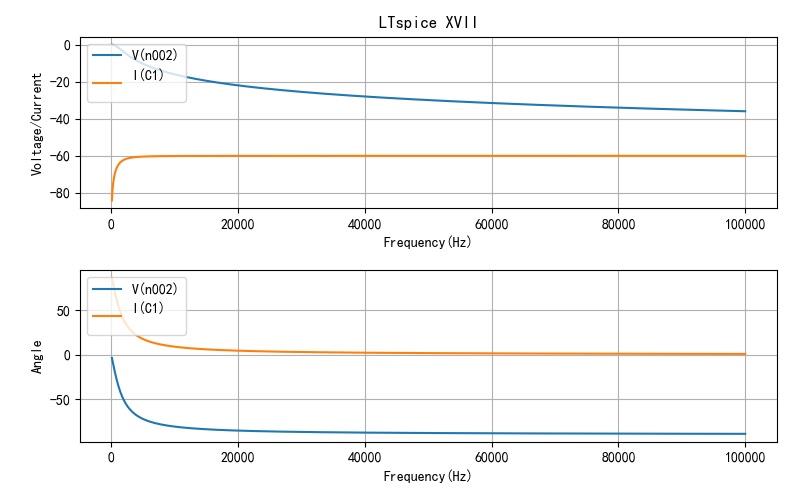
▲ 图1.1.2 LTspice 仿真结果
3、理论分析
根据电路提,可以知道对于不同频率,系统传递函数为:
H ( j ω ) = 1 1 + j ω R C H\\left( j\\omega \\right) = 1 \\over 1 + j\\omega RC H(jω)=1+jωRC1
其中: R = 1000 Ω ; C = 0.1 μ F R = 1000\\Omega ;\\,\\,\\,C = 0.1\\mu F R=1000Ω;C=0.1μF 。根据上面公式计算出输出的幅值和相位,对比仿真的结果,可以看到他们之间是相符的。下图分别绘制出仿真的结果与理论计算的结果, 他们是重叠的。
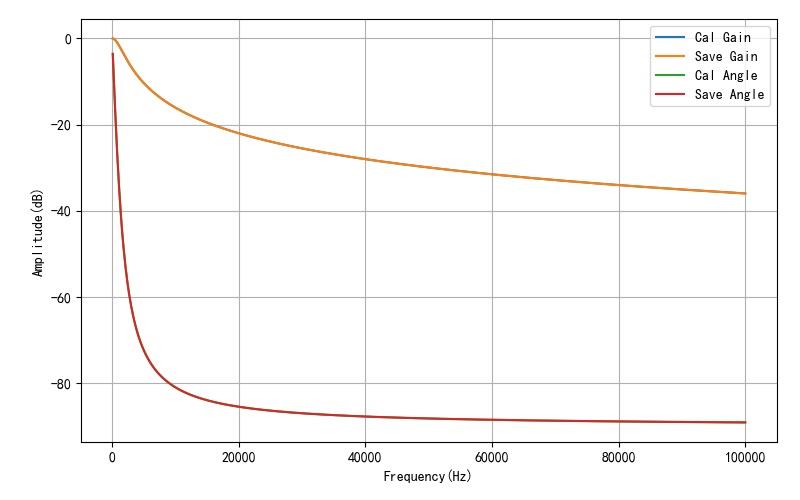
▲ 对比理论分析与仿真结果
#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST2.PY -- by Dr. ZhuoQing 2022-08-15
#
# Note:
#============================================================
from headm import *
data, angle1 = tspload('ltsdata', 'data', 'angle')
R = 1e3
C = 0.1e-6
f = linspace(1e2, 100e3, 1000)
outf = [1/(1+1j * 2 * pi * ff * R * C) for ff in f]
gain = [log(abs(o))/log(10)*20 for o in outf]
angle11 = [angle(o)*180/pi for o in outf]
plt.plot(f, gain, label='Cal Gain')
plt.plot(data[0], data[1], label='Save Gain')
plt.plot(f, angle11, label='Cal Angle')
plt.plot(data[0], angle1[1], label='Save Angle')
plt.xlabel("Frequency(Hz)")
plt.ylabel("Amplitude(dB)")
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
#------------------------------------------------------------
# END OF FILE : TEST2.PY
#============================================================
二、全通系统
1、电路分析
下面是在信号与系统中给出的全通电路原理图以及对应的公式。
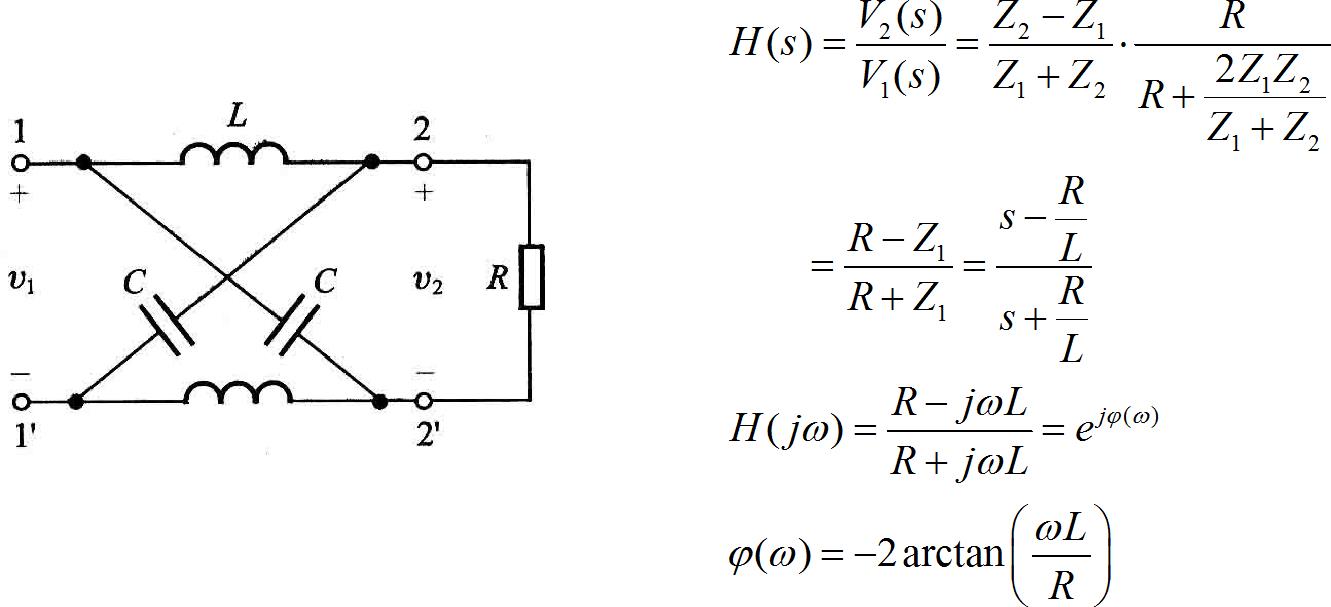
▲ 图1.2.1 信号与系统中列举的全通系统电路
为了求解上述电路,将电路还原成原来的桥式电路。令: Z 1 = j ω L , Z 2 = 1 / j ω C Z_1 = j\\omega L,Z_2 = 1/j\\omega C Z1=jωL,Z2=1/jωC 。利用戴维南电源等效原理,从两个桥臂中间往外,可以等效成一个电压源串联一个内阻。内阻等于 Z 1 , Z 2 Z_1 ,Z_2 Z1,Z2 的并联, 那么两个内阻对外就等于: R 0 = 2 Z 1 Z 2 Z 1 + Z 2 R_0 = 2Z_1 Z_2 \\over Z_1 + Z_2 R0=Z1+Z22Z1Z2
两个桥臂中间的分压 V 1 , V 2 V_1 ,V_2 V1,V2 为:
V 1 = Z 2 Z 1 + Z 2 ⋅ V i n ; V 2 = Z 1 Z 1 + Z 2 ⋅ V i n V_1 = Z_2 \\over Z_1 + Z_2 \\cdot V_in ;\\,\\,V_2 = Z_1 \\over Z_1 + Z_2 \\cdot V_in V1=Z1+Z2Z2⋅Vin;V2=Z1+Z2Z1⋅Vin
所以电压源为:
V
12
=
V
1
−
V
2
=
Z
2
−
Z
1
Z
1
+
Z
2
V
i
n
V_12 = V_1 - V_2 = Z_2 - Z_1 \\over Z_1 + Z_2 V_in
V12=V1−V2=Z1+Z2Z2−Z1Vin 对应的输出为:
H
(
s
)
=
Z
2
−
Z
1
Z
1
+
Z
2
⋅
R
R
+
2
Z
2
Z
1
Z
1
+
Z
2
=
R
(
Z
2
−
Z
1
)
R
(
Z
1
+
Z
2
)
+
2
Z
1
Z
2
H\\left( s \\right) = Z_2 - Z_1 \\over Z_1 + Z_2 \\cdot R \\over R + 2Z_2 Z_1 \\over Z_1 + Z_2 = R\\left( Z_2 - Z_1 \\right) \\over R\\left( Z_1 + Z_2 \\right) + 2Z_1 Z_2
H(s)=Z1+Z2Z2−Z1⋅R+Z1+Z22Z2Z1R=R(Z1+Z2)+2Z1Z2R(Z2−Z1)
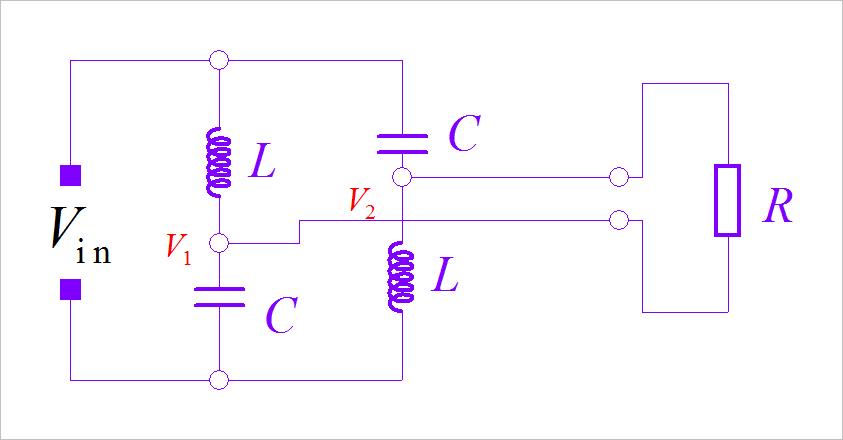
▲ 图1.2.2 桥式输出电路
在往后推导,参见 Lattice phase equaliser ,对于这个网络的推导还是存在的疑惑的。