跟着开源项目学因果推断——CausalImpact 贝叶斯结构时间序列模型(二十一)
Posted 悟乙己
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了跟着开源项目学因果推断——CausalImpact 贝叶斯结构时间序列模型(二十一)相关的知识,希望对你有一定的参考价值。
文章目录
1 Causal Impact与贝叶斯结构时间序列模型
1.1 观测数据下Causal Impact的背景由来
非随机化的效果评估方法(二)
一图讲清因果推断方法论,无法 AB 测试时分析的万能钥匙
下图汇总了目前解决各个分析场景的方法论框架:
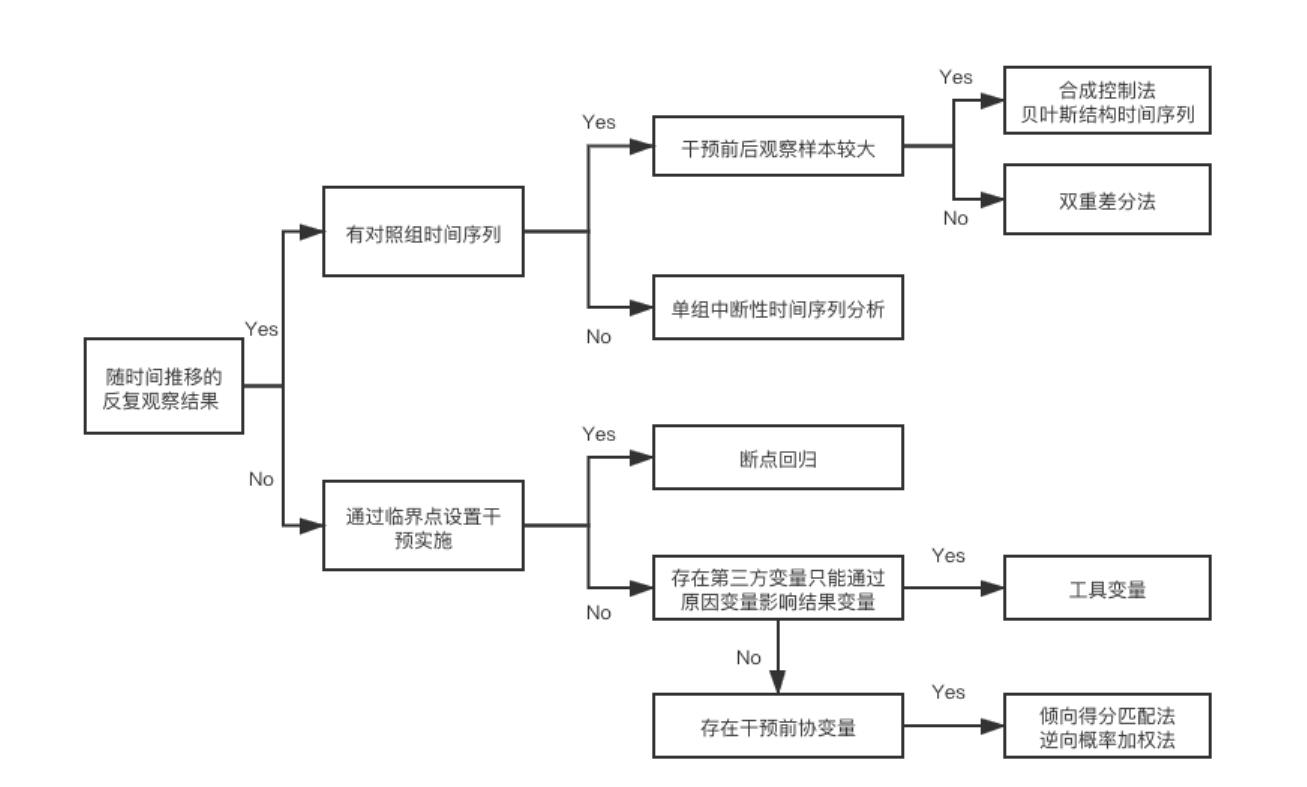
一些无法进行随机实验的场景下,会需要合成控制的方式
大部分运营和产品在评估效果时,最常用的方法就是effect = 上线后效果-上线前效果。这种方法最大的问题在于其关键假设,即上线的功能或者活动是唯一影响效果的变量。但是想想就知道这个假设是有多么不合理。
升级版的评估方案,可能会找到一个城市或者大盘来和上线的城市做对比,这种想法非常类似DID,但是这个里面也隐含着一个关键假设,即可以找到长期变化趋势高度同步的城市,这点对于有较强地域性的商业来说就非常困难。
更加升级版的方案可能是不需要找到一个变化趋势非常趋同的城市,而且通过类似集成学习的方法,将多个城市作为输入,并结合自身长期的时间序列波动来拟合出一个策略没上线的虚拟现实。使寻找高度同步的城市从一个强假设变成一个弱假设。Causal Impact就是这种思想的一个具体实践。
Causal Impact是基于贝叶斯结构时间序列模型,会综合多种信息输入结合自身的时间序列来构造一个策略未上线的虚拟值,以一个案例来进行说明。
1.2 贝叶斯结构时间序列模型
1.3 谷歌的Causal Impact
数据分析36计(12):做不了AB测试,如何量化评估营销、产品改版等对业务的效果.
在不能做AB测试的情况下,产品上线后做效果评估一般会直接选择上线前后的指标做对比,但是不同时期的指标本身受到的影响不一样,比如节假日、季节性影响,使得选择上线前后时间段的指标比较主观。
为了准确的量化产品改版的效果,谷歌推出了开源项目causalimpact工具包,该方法基于合成控制法的原理,利用多个对照组数据来构建贝叶斯结构时间序列模型,并调整对照组和实验组之间的大小差异后构建综合时间序列基线,最终预测反事实结果。即如果没有上线这次的产品改版,那么产品指标该是如何走向。那么这次的产品改版对指标的影响大小即是真实值(产品改版后的指标值)和预测值(预测没有改版该时期的指标值)的差距。
那么该方法中需要准备:
1、时间序列数据
待评估指标在每日或每周或每小时的值,作为方法的输入值,该方法会拟合产品上线前的指标数据进行预测,得到新的时间序列,那么这段新的时间序列和产品上线后指标的真实值差距就是该产品改版的效果。
2、对照组时间序列
在预测前可找到相似趋势的时间序列数据加入模型中,已知相似时间序列可以作为预测序列中的趋势效应,皮尔逊相关系数可以作为时间序列相似性的度量。
3、为达到预测准确需要的数据探索
时间序列本身是由长期趋势、季节性因素、周期性因素和随机变动因素组成(如下图),为了预测准确,需要识别历史数据的这些特征,才能更准确的预测时间序列。
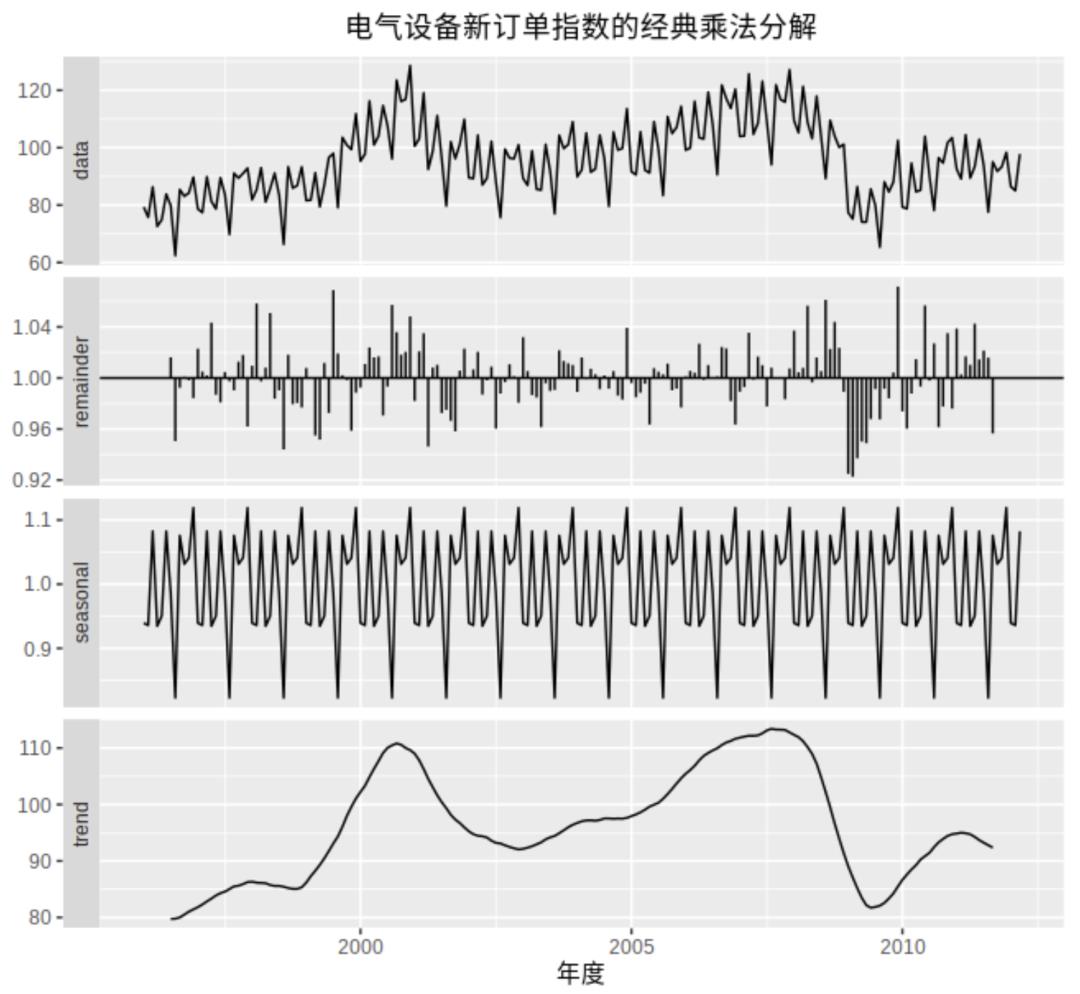
- 趋势,即在一定时间内的单调性,一般来说斜率是固定的。
- 周期性,与季节性很像,但是它的波动的时间频率不是固定的。因为其波动频率不固定,一般会与趋势一起分析而不做拆分,比如上图中trend曲线,跌落谷底之后又反弹,这种往复的运动,被称之为周期性。
- 季节性,固定长度的变化,就像春夏秋冬的温度变化一样。比如上图中每12个月就会出现一次周期循环,不同年中每个月的值都大致相等。
- 节假日,业务通常也会受节假日的影响最终反映在指标的波动上。为了在历史数据中识别出节假日的效应,模拟数据最好有一年的历史数据。
2 一些案例
2.1 CausalImpact的时序选择
外卖公司在A城对外卖骑手上线了S策略以提升拼单率,由于策略管控类实验不能对骑手进行歧视,因此不能够进行AB实验,必须全量上线,需评估策略效果。
CausalImpact构建分为两个步骤:
· 控制的时间序列选择:
通过dtw算法选择与A城拼单率最相似的时间序列,通过距离的计算得到B城干预前的拼单率时间序列与A城最为接近。
· 通过观察拟合后的结果,判断策略是否与显著效果
第一张图(original)黑色实线为A城在策略上线前后的实际结果,蓝色虚线为根据B城拟合的A城结果,也就是模拟的策略未上线时A城结果,蓝色区域为置信区间。
第二张图(pointwise)蓝色虚线为A城策略前后拼单率的差值,可以看到策略上线后,拼单率差值是显著为正的。
第三张图(cumulative)蓝色虚线为策略上线后的累加值,是持续增大的,可见策略有明显的正向作用。
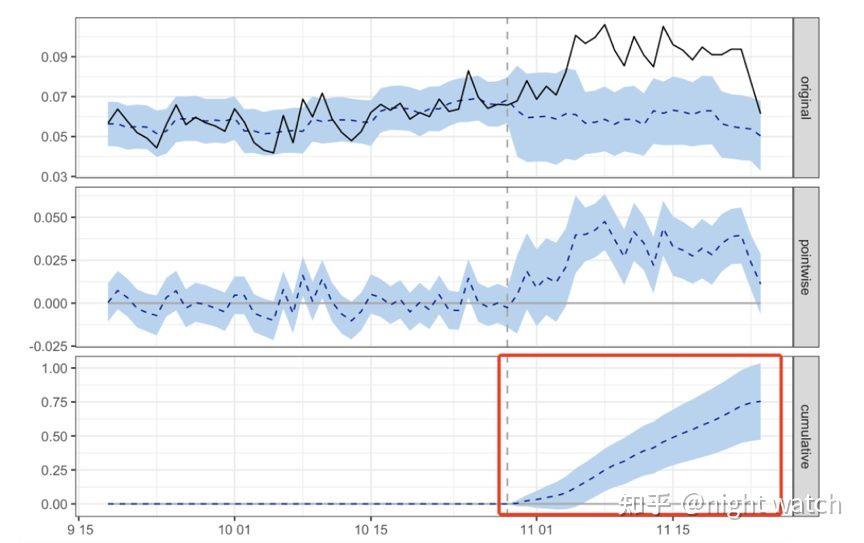
下图为具体的策略效果:
拼单率日均提升3pp
笔者再多解读一些下面的图:
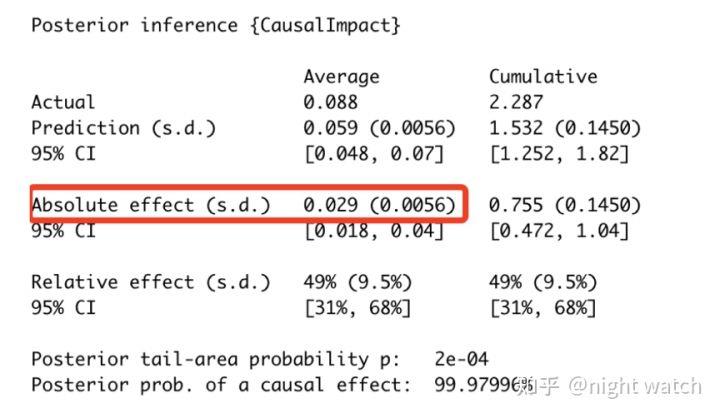
- 第一个数据模块:实验最终的平均预测值(
prediction)为0.059,平均实际值(actual)为0.088;而累计预测值1.532,累计实际值2.287;这里的平均数据范围就是上述虚线之后的时间段- 第二个数据模块:经过MCMC估计指标绝对效应(
absolute effect)平均增长0.029,累计增长0.755;相对比率(relative effect)平均增长49%,累计增长49%
CausalImpact有三个要点:
- 一是在模型拟合过程中(original),AA差异的置信区间要始终包含0,相当于模型的拟合误差在我们的接受范围之内,反之则说明模型的拟合误差过大,模型不可信;
- 二是策略上线后(pointwise),每天的收益水平是否包含0 ,如果包含0则说明收益是不显著的;
- 三是策略长期收益(cumulative),有的策略存在新奇效应,不能得到长期收益,所以需关注累积收益进行决策。
2.2 日文案例:CausalImpactの理解と実装
論文:https://ai.google/research/pubs/pub41854
python実装:https://github.com/dafiti/causalimpact
案例地址:https://github.com/rmizuta3/causalimpact/blob/master/causalimpact_restaurant.ipynb
传统几种在观测数据的工作流(差分差分法+ synthetic control method):
- 选择一个以上符合条件的对照组
- 使用synthetic control method来选择对照组(如果一个有多个)
synthetic control method是通过使多个对照组的加权之和尽量接近处置组,创建假想未处置时的处置组的方法。 - 使用DID,比较处理组和在2中制作的对照组
上述工作流程的问题点:
- 时间序列数据一般都会产生自回归分量,但DID的假设是各时间点独立同分布。
- 由于DID只能观察两点之间的差异,例如,假设活动持续了一周,那么就无法单独观察活动开始和结束前的影响。
- 由于进行synthetic control method→差分的差分法这两个阶段的推算,很难判断哪个阶段的误差影响更大。
CausalImpact的方法介绍:
- 使用状态空间模型,从对照组中生成未采取措施时的对照组,计算出预测值。
- 将其与实际处置组的值进行比较,计算出因果效果。
CausalImpact的亮点:
- 使用状态空间模型可以考虑自回归成分和季节性等时间序列因素
- 可以确认时间序列中每一点的影响
- synthetic control method的部分和DID所做的事情用一个状态空间模型来覆盖,所以很容易知道哪个部分发生了误差。了解模型的不确定性。
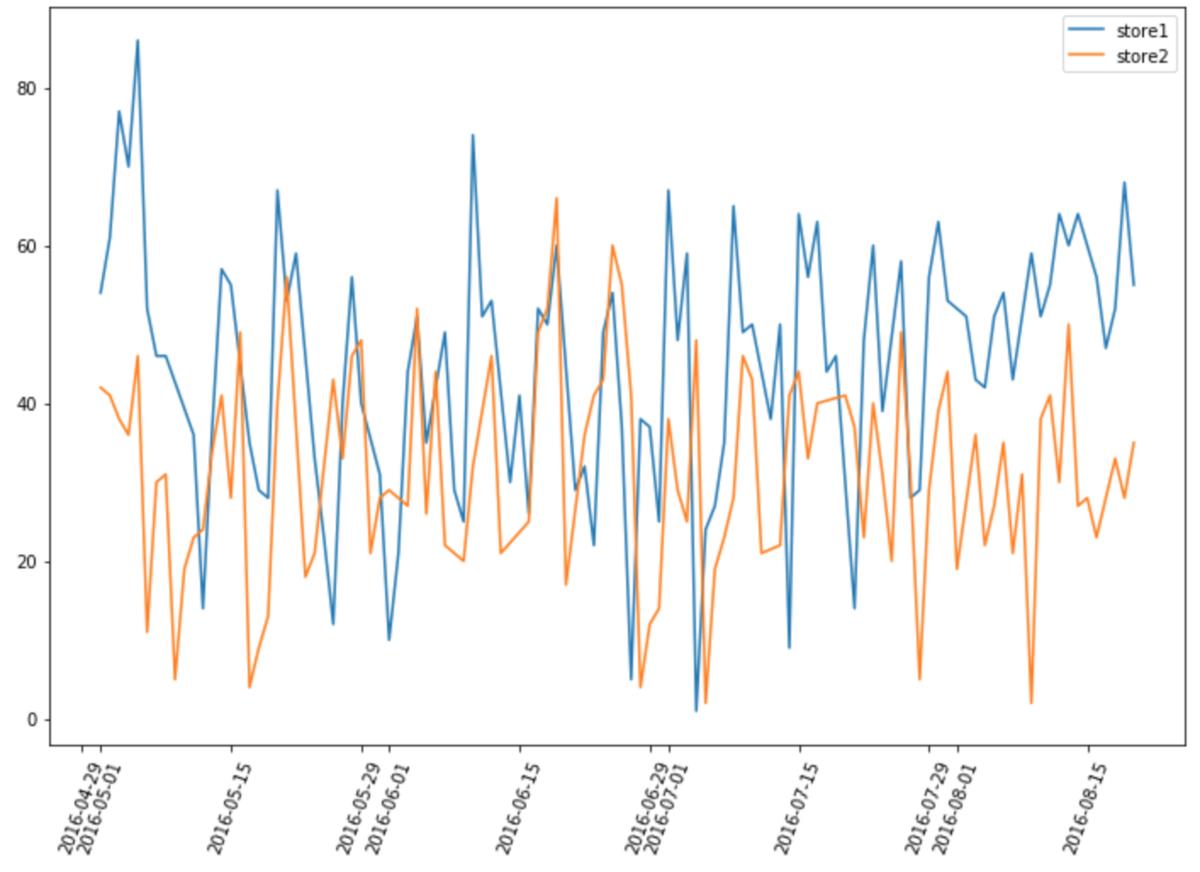
使用的数据和上次使用差分差分法时一样,使用Recruit Restaurant Visitor Forecasting餐厅的来店人数数据,来测定某店铺在盂兰盆节期间(8/11-20)的影响效果。
两家店铺的布局图是这样的。
这里是数据处理的过程:
df=pd.read_csv("air_visit_data.csv",parse_dates=["visit_date"])
#元のデータは欠損があるため日時のベースを作成
basedate=pd.DataFrame(list(pd.date_range('2016-05-01', '2016-08-20')))
basedate.columns=["visit_date"]
#店舗を指定、日時を限定
store1=df[df["air_store_id"]=="air_e55abd740f93ecc4"]
store1=store1[(store1["visit_date"]>="2016-05") & (store1["visit_date"]<="2016-08-20")]
store2=df[df["air_store_id"]=="air_1653a6c513865af3"]
store2=store2[(store2["visit_date"]>="2016-05") & (store2["visit_date"]<="2016-08-20")]
#データを結合
store1.rename(columns="visitors":"visitors_store1",inplace=True)
store2.rename(columns="visitors":"visitors_store2",inplace=True)
data=pd.merge(basedate,store1[["visit_date","visitors_store1"]],on="visit_date",how="left")
data=pd.merge(data,store2[["visit_date","visitors_store2"]],on="visit_date",how="left")
data=data.interpolate() #欠損値を線形補間
data=data.set_index("visit_date")
pre_period 和 post_period 分别代表观测时间段,预测时间段;
因为按周来看影响,所以这里nseason为7。
from causalimpact import CausalImpact
pre_period = ['2016-05-01', '2016-08-10']
post_period = ['2016-08-11', '2016-08-20']
ci = CausalImpact(data, pre_period, post_period,nseasons=['period': 7],trend=True)
print(ci.summary())
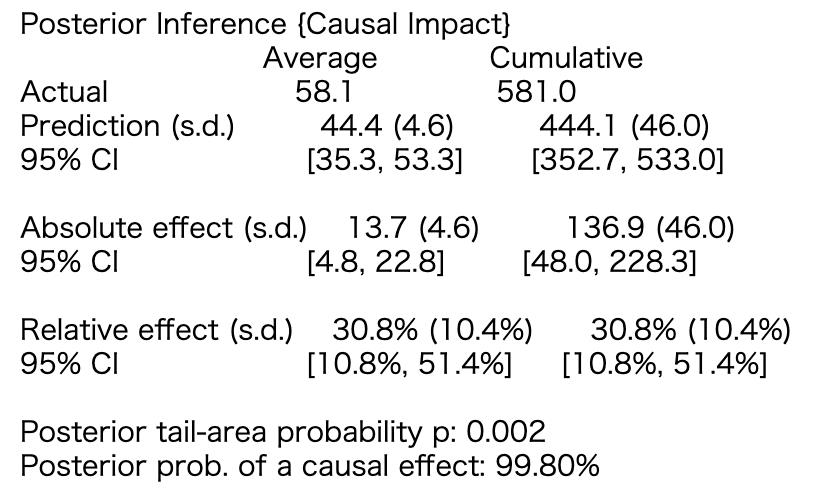
盂兰盆节的效果是平均13.7人,10天累积下来有137人的效果。
使用DID时,得出的数值是13.5人,所以得出的数值差不多。95%置信区间也算出来了,累计来看48.0 ~ 228.3,可以看出结构模型并不稳定。
能看到结果有多不确定性是很好的。
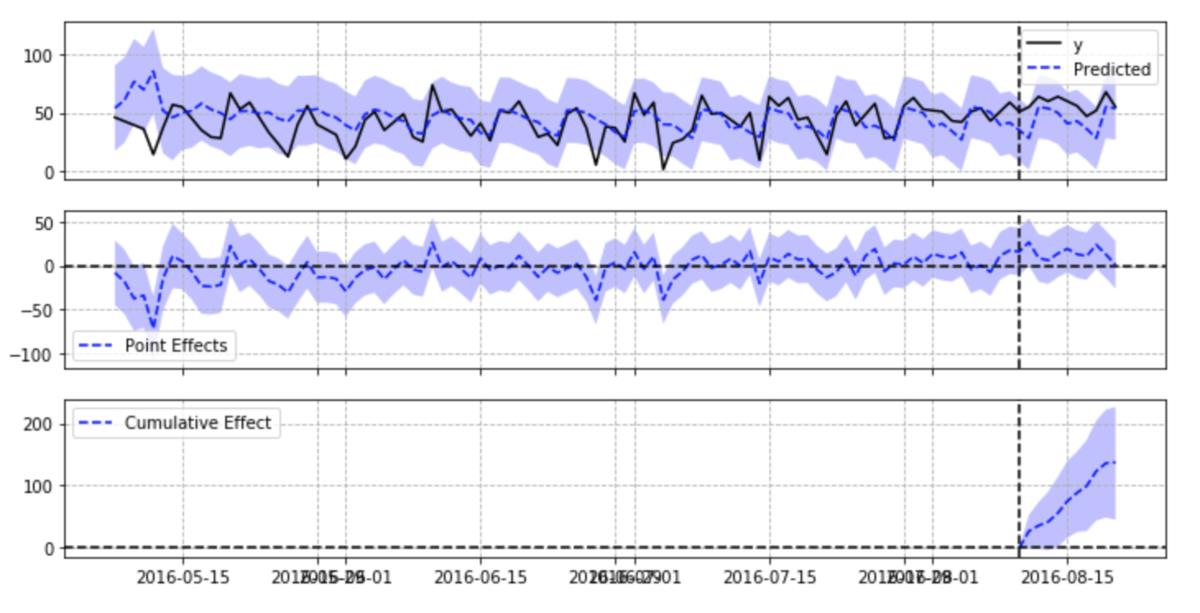
第一张图中y是处置组,Predicted是状态空间模型的预测值,有颜色的部分是预测值的置信区间。
第二个图表表示第一个图表的y-Predicted。
第三个图表表示处置期间y-Predicted的累计和。
顺便说一下,CausalImpact包含了UnobservedComponents,可以查看状态空间模型本身的结果。
ci.trained_model.summary()
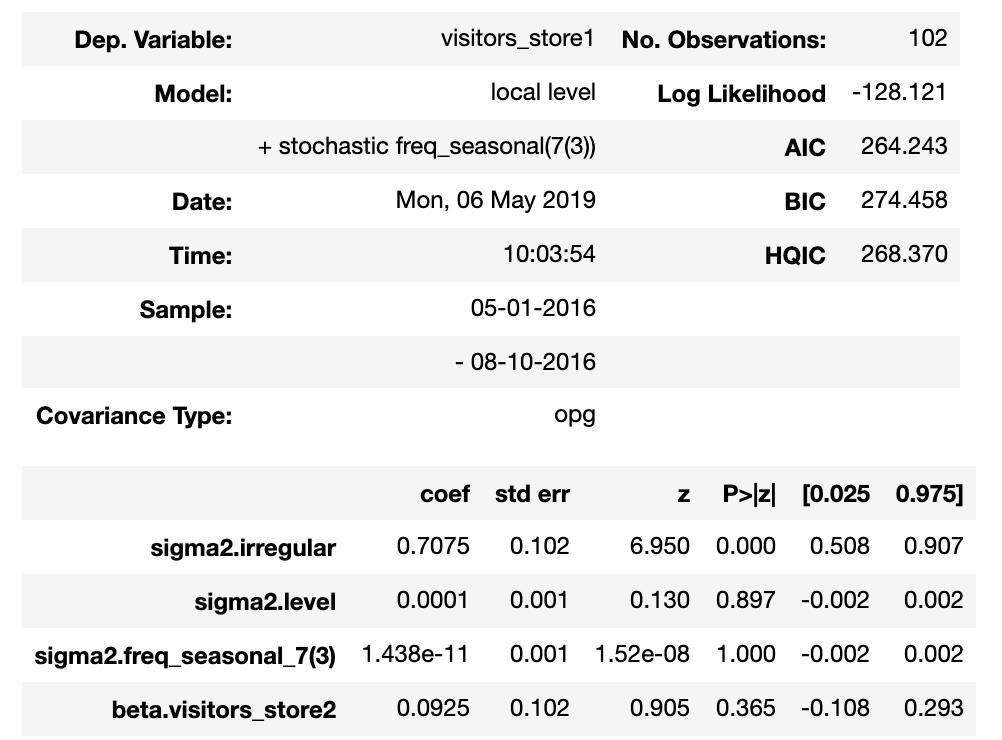
因为创建的状态空间模型的观测误差很大,所以置信区间变得很广。
CausalImpact通常需要输入对照组,但如果没有也可以使用。
这种情况下状态空间模型从实验组的时序开始进行拟合创建。
pre_period = ['2016-05-01', '2016-08-10']
post_period = ['2016-08-11', '2016-08-20']
ci = CausalImpact(data.iloc[:,0], pre_period, post_period,nseasons=['period': 7])
ci.plot(figsize=(12, 6))
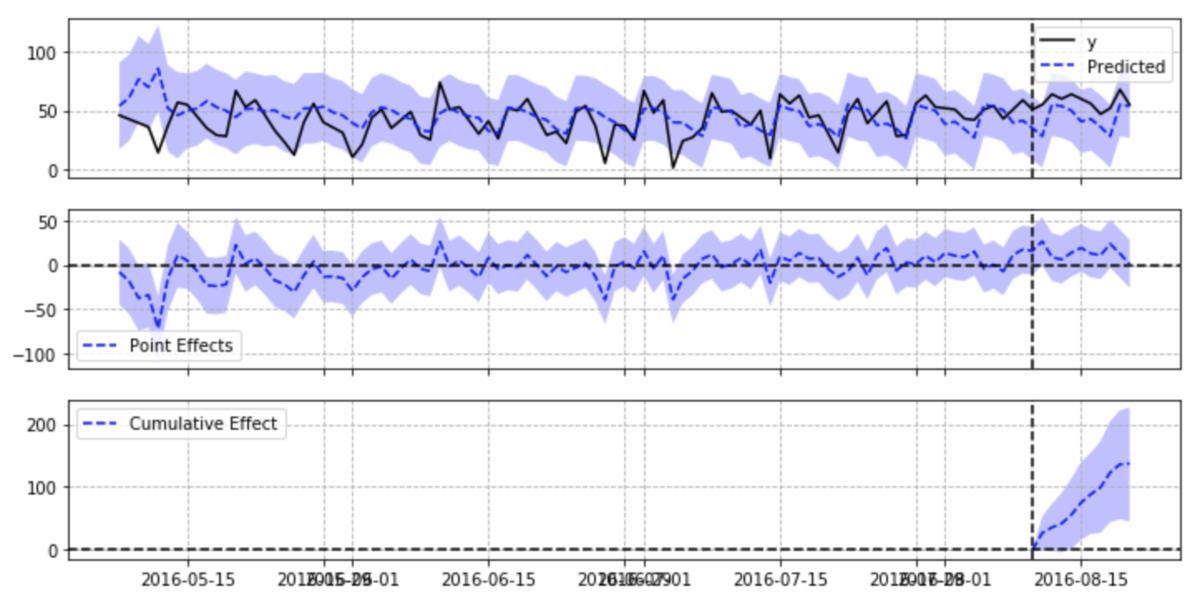
这次的例子和加入对照组的结果没有太大区别。如果对照组可以输入多个数据,结果可能会比较稳定。
很高兴能得出效果的置信区间
因为可以对每一个点进行推测,所以也可以看到处理区间内的变化,这似乎不错。
当你不能输入多个对象时,它可能不会发挥作用。
2.3 [翻译]R语言案例:An R package for causal inference using Bayesian structural time-series models
An R package for causal inference using Bayesian structural time-series models
该包的设计目的是使反事实推理像拟合回归模型一样简单,但在满足上述假设的情况下,功能要强大得多。该包只有一个入口点,即函数CausalImpact()。给定一个响应时间序列和一组控制时间序列,该函数构造一个时间序列模型,对反事实进行后验推理,并返回一个CausalImpact对象。结果可以用表格、文字描述或图表来概括。
# 创建数据
set.seed(1)
x1 <- 100 + arima.sim(model = list(ar = 0.999), n = 100)
y <- 1.2 * x1 + rnorm(100)
y[71:100] <- y[71:100] + 10
data <- cbind(y, x1)
pre.period <- c(1, 70)
post.period <- c(71, 100)
# 画图
impact <- CausalImpact(data, pre.period, post.period)
plot(impact)
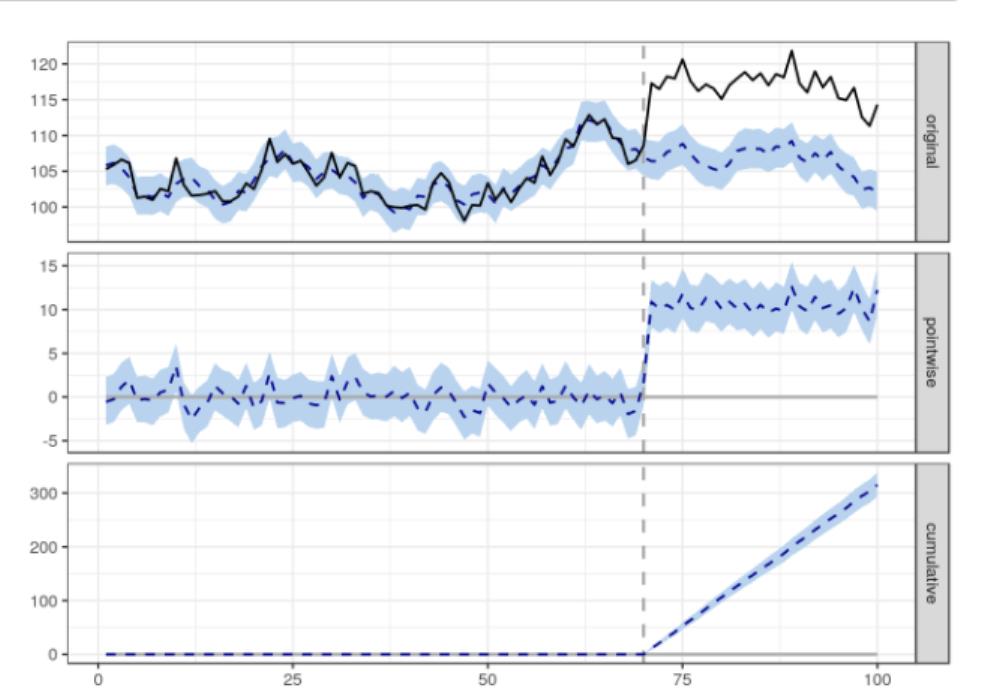
默认情况下,该绘图包含三个面板。
第一个面板显示数据和一个反事实的预测后治疗时期。
第二个面板显示了观测数据和反事实预测之间的差异。这是由模型估计的点态因果效应。
第三组将第二组的逐点贡献相加,得出干预的累积效应。
记住,再一次,所有以上的推论都依赖于一个假设,即协变量本身不受干预的影响。
该模型还假设在前一时期建立的协变量和处理时间序列之间的关系,在整个后一时期保持稳定。
3 官方:TensorFlow Causal Impact
官网地址:getting_started
3.1 背景
谷歌开发的影响模型的工作原理是将贝叶斯结构时间序列模型与观测数据进行拟合,这些数据后来被用来预测在给定的时间段内,如果没有干预,将会产生什么结果,如下图所示:
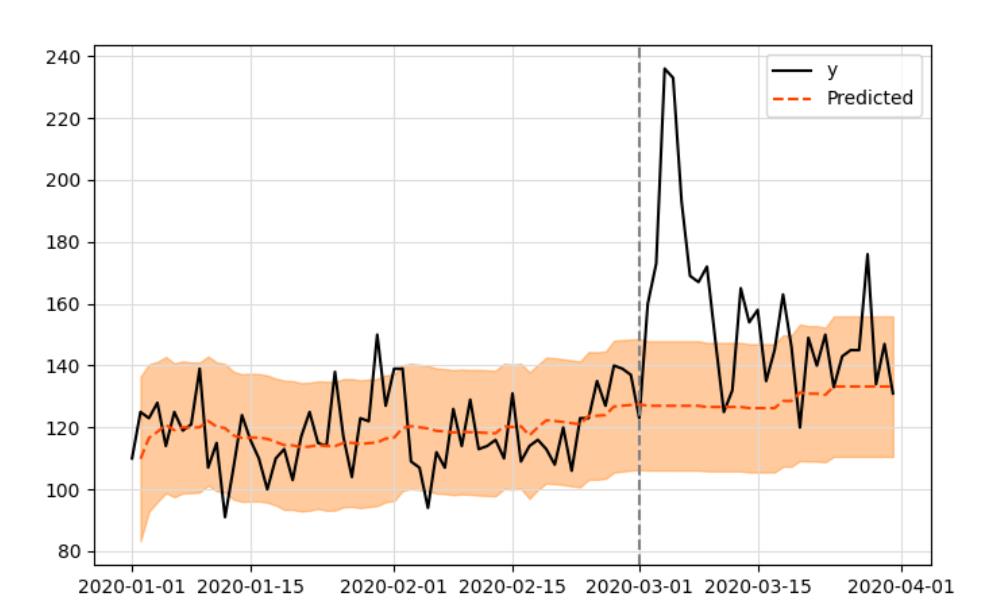
这个想法是使用拟合模型的预测(用橙色表示)作为一个参考,在没有干预发生的情况下,可能会观察到什么。
贝叶斯结构时间序列模型可以用以下公式表示:
y
t
=
Z
t
T
α
t
+
β
X
t
+
G
t
ϵ
t
y_t = Z^T_t\\alpha_t + \\beta X_t + G_t\\epsilon_t
yt=ZtTαt+βXt+Gtϵt
a
t
+
1
=
T
t
α
t
+
R
t
η
t
a_t+1 = T_t\\alpha_t + R_t\\eta_t
at+1=Ttαt+Rtηt
ϵ
t
∼
N
(
0
,
σ
t
2
)
\\epsilon_t \\sim \\mathcalN(0, \\sigma_t^2)
ϵt∼N(0,σt2)
η
t
∼
N
(
0
,
Q
t
)
\\eta_t \\sim \\mathcalN(0, Q_t)
ηt∼N(0,Qt)
a也被称为系列的“状态”,yt是状态的线性组合加上协变量X的线性回归(以及遵循零均值正态分布的测量噪声ϵ)。
通过改变矩阵Z、T、G和R,我们可以为时间序列建模几个不同的行为(包括更著名的ARMA或ARIMA)。
在这个包中(谷歌的R包也是如此),您可以选择任何您想要适合您的数据的时间序列模型(下面将详细介绍)。如果没有使用模型作为输入,则默认构建一个local level,这意味着yt表示为:
y
t
=
μ
t
+
γ
t
+
β
X
t
+
ϵ
t
y_t = \\mu_t + \\gamma_t + \\beta X_t + \\epsilon_t
yt=μt+γt+βXt+ϵt
μ
t
+
1
=
μ
t
+
η
μ
,
t
\\mu_t+1 = \\mu_t + \\eta_\\mu, t
μt+1=μt+ημ,t
-
μ t \\mu_t μt变量,自回归的过程,任何给定的时间点首先由随机游走分量 μ t \\mu_t μt建模,也被称为“local level”分量,自回归的环节也没有新增什么额外的协变量信息
-
模拟季节成分的 γ t \\gamma_t γt变量
-
我们有分量 β X t \\beta X_t βXt这是协变量的线性回归,进一步有助于解释观测数据。该组件在预测任务中越显著, μ t \\mu_t μt变量的影响就越小,是有相对关系的。
-
参数 ϵ t \\epsilon_t ϵt模拟与测量 y t y_t yt相关的噪声,它遵循零均值和 σ ϵ \\sigma_\\epsilon σϵ标准差的正态分布。
生成数据:
%matplotlib inline
import sys
import os
sys.path.append(os.path.abspath('../'))
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
from causalimpact import CausalImpact
tfd = tfp.distributions
plt.rcParams['figure.figsize'] = [15, 10]
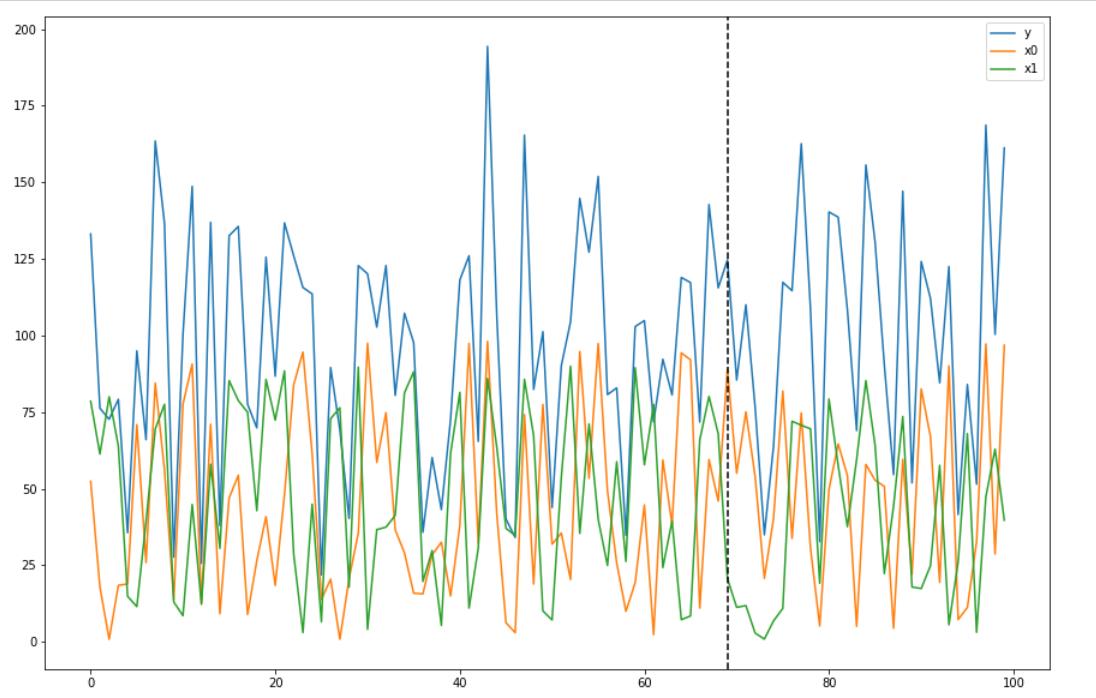
# 生成数据
# This is an example presented in Google's R code.
# Uses TensorFlow Probability to simulate a random walk process.
observed_stddev, observed_initial = (tf.convert_to_tensor(value=1, dtype=tf.float32),
tf.convert_to_tensor(value=0., dtype=tf.float32))
level_scale_prior = tfd.LogNormal(loc=tf.math.log(0.05 * observed_stddev), scale=1, name='level_scale_prior')
initial_state_prior = tfd.MultivariateNormalDiag(loc=observed_initial[..., tf.newaxis], scale_diag=(tf.abs(observed_initial) + observed_stddev)[..., tf.newaxis], name='initial_level_prior')
ll_ssm = tfp.sts.LocalLevelStateSpaceModel(100, initial_state_prior=initial_state_prior, level_scale=level_scale_prior.sample())
ll_ssm_sample = np.squeeze(ll_ssm.sample().numpy())
x0 = 100 * np.random.rand(100)
x1 = 90 * np.random.rand(100)
y = 1.2 * x0 + 0.9 * x1 + ll_ssm_sample
y[70:] += 10
data = pd.DataFrame('x0': x0, 'x1': x1, 'y': y, columns=['y', 'x0', 'x1'])
data.plot()
plt.axvline(69, linestyle='--', color='k')
plt.legend();
3.2 默认模型
使用默认的模型:
pre_period = [0, 69]
post_period = [70, 99]
ci = CausalImpact(data, pre_period, post_period)
ci.plot()
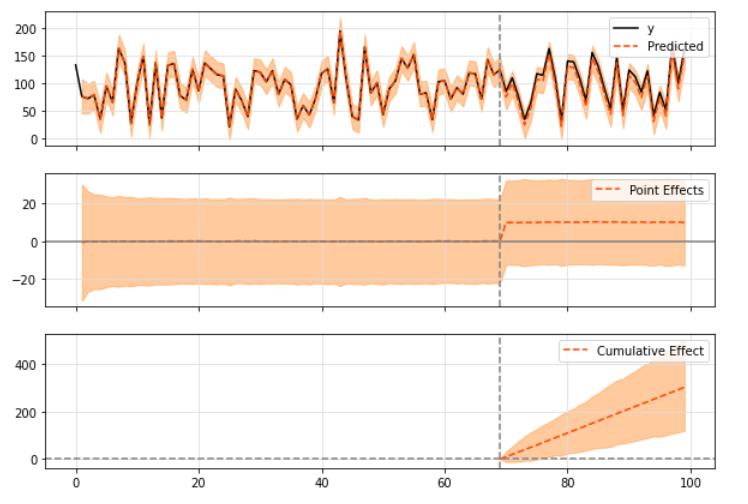
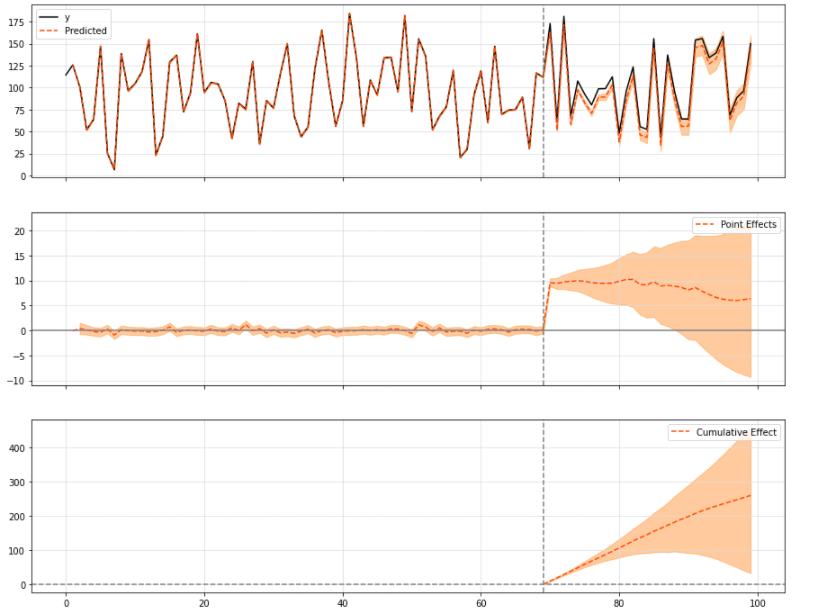
绘制结果时,默认打印三种图形:
- “原始”系列与预期的系列
- “点效应”(即原始序列和预测序列之间的差异)
- 最后是“累积”效应,它基本上是点效应随时间累积的总和。
您可以选择打印上面图中三个模块的某些模块:
ci.plot(panels=['original', 'pointwise'], figsize=(15, 12))
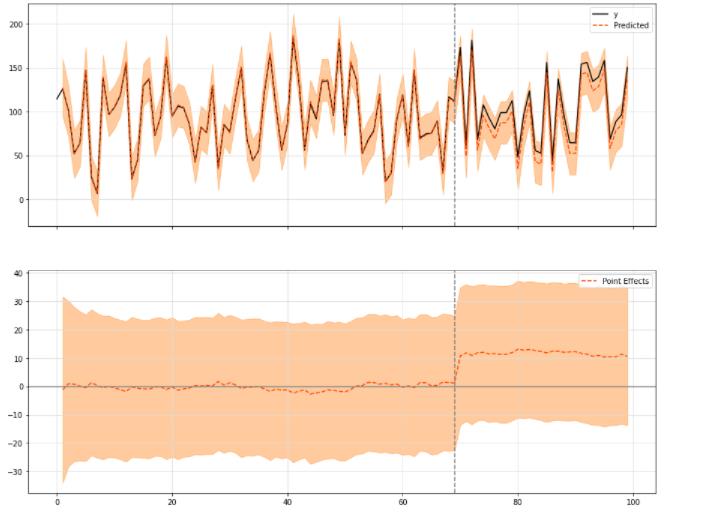
为了查看一般的结果和数字,你可以调用带有默认输入或“报告”的summary方法,它会打印出观察到的效果的更详细的解释:
print(ci.summary())
结果为:
Posterior Inference Causal Impact
Average Cumulative
Actual 106.01 3180.15
Prediction (s.d.) 96.16 (3.6) 2884.67 (107.86)
95% CI [89.16, 103.25] [2674.67, 3097.47]
Absolute effect (s.d.) 9.85 (3.6) 295.49 (107.86)
95% CI [2.76, 16.85] [82.69, 505.48]
Relative effect (s.d.) 10.24% (3.74%) 10.24% (3.74%)
95% CI [2.87%, 17.52%] [2.87%, 17.52%]
Posterior tail-area probability p: 0.0
Posterior prob. of a causal effect: 99.6%
For more details run the command: print(impact.summary('report'))
例如,我们可以在这里看到,观察到的绝对效应大约是9,其预测在95%置信区间从2到15之间变化。
这个置信区间的差异,还是蛮大的
当观察这些结果时,一个非常重要的数字是p值,
P值通过,可以证明确实存在因果效应的概率(而不仅仅是噪声)。
所以,当作一次假设检验来看。
如果你想要一个更详细的总结,运行以下命令:
print(ci.summary(output='report'))
具体可见:
Analysis report CausalImpact
During the post-intervention period, the response variable had
an average value of approx. 106.01. By contrast, in the absence of an
intervention, we would have expected an average response of 96.16.
The 95% interval of this counterfactual prediction is [89.16, 103.25].
Subtracting this prediction from the observed response yields
an estimate of the causal effect the intervention had on the
response variable. This effect is 9.85 with a 95% interval of
[2.76, 16.85]. For a discussion of the significance of this effect,
see below.
ci还有很多信息,比如,每一个序列的:
ci.inferences.head()

print('Mean value of noise observation std: ', ci.model_samples[0].numpy().mean())
print('Mean value of level std: ', ci.model_samples[1].numpy().mean())
print('Mean value of linear regression x0, x1: ', ci.model_samples[2].numpy().mean(axis=0))
3.3 设定一些规范
3.3.1 设定先验标准差
这里还可以设定一些数字上的规范,比如先验标准差控制在某个范围内。这里有一个例子:
ci = CausalImpact(data, pre_period, post_period, model_args='prior_level_sd':0.1)
ci.plot(figsize=(15, 12))
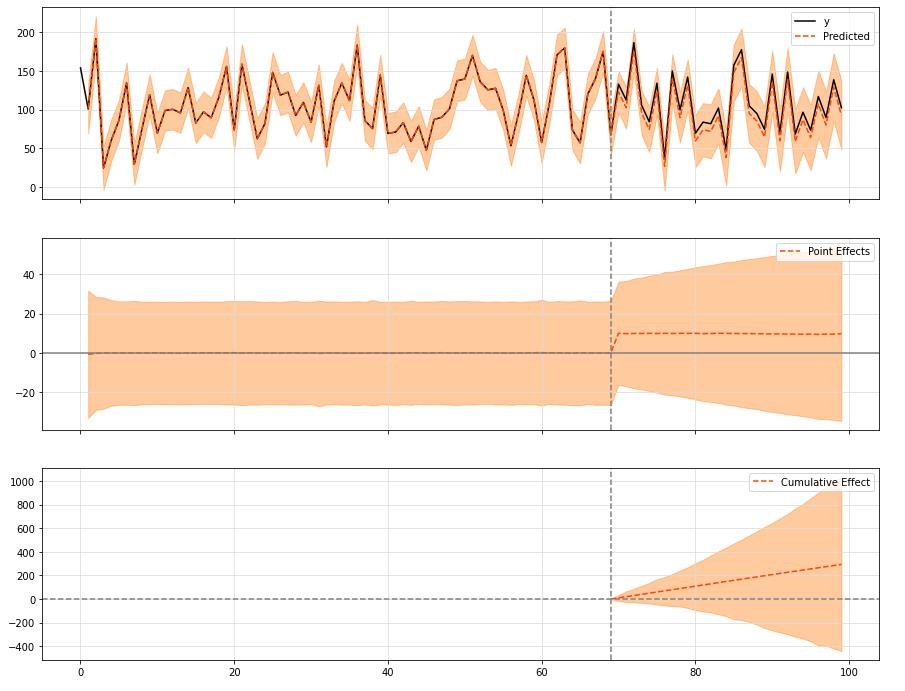
默认值是
0.01
0.01
0.01,表示数据表现良好,方差小,并且可以很好地解释协变量。
如果事实证明对于给定的输入数据并非如此,则可以更改本地标准偏差的先验值,以反映数据中的这种模式。
对于
0.1
0.1
0.1的值,我们基本上是说,数据中有一个更强的随机游走成分,不能用协变量本身来解释。
3.3.2 设定季节因素
observed_stddev, observed_initial = (5., 0.)
num_seasons = 7
drift_scale_prior = tfd.LogNormal(loc=tf.math.log(.01 * observed_stddev), scale=1.)
initial_effect_prior = tfd.Normal(loc=observed_initial, scale=tf.abs(observed_initial) + observed_stddev)
initial_state_prior = tfd.MultivariateNormalDiag(loc=tf.stack([initial_effect_prior.mean()] * num_seasons, axis=-1),
scale_diag=tf.stack([initial_effect_prior.stddev()] * num_seasons, axis=-1))
s_ssm = tfp.sts.SeasonalStataeSpaceModel(
num_timesteps=100,
num_seasons=num_seasons,
num_steps_per_season=1,
drift_scale=drift_scale_prior.sample(),
initial_state_prior=initial_state_prior
)
plt.plot(s_ssm.sample());
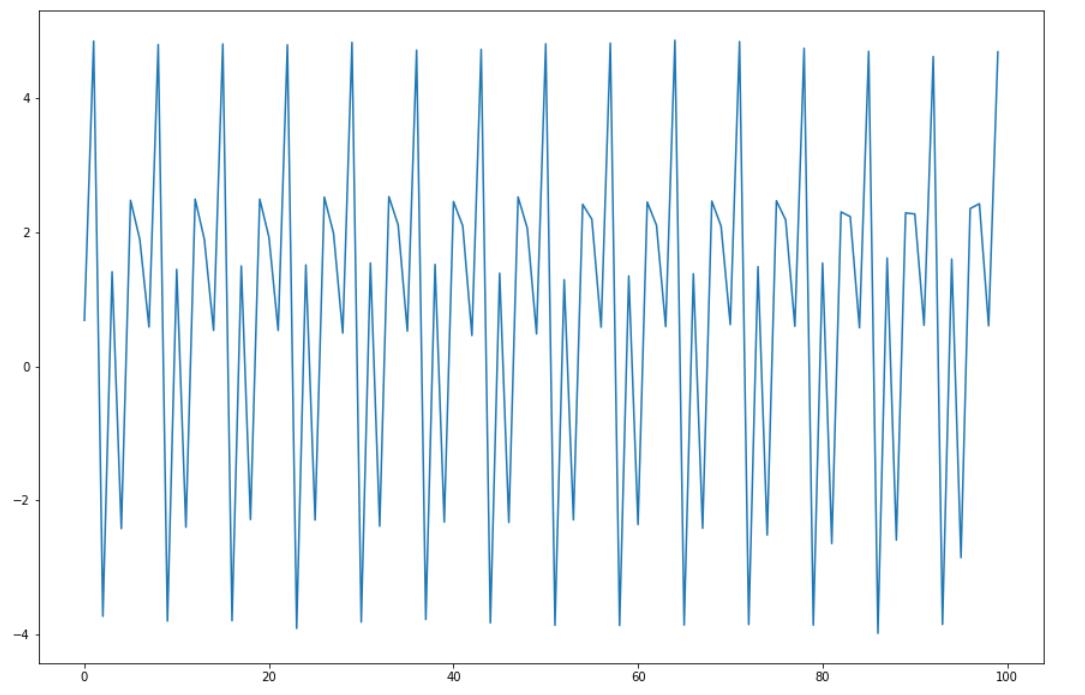
season_data = data.copy()
season_data['y'] += np.squeeze(s_ssm.sample().numpy())
ci = CausalImpact(season_data, pre_period, post_period, model_args='nseasons': 7)
print(ci.summary())
ci.plot()
输出:
Posterior Inference Causal Impact
Average Cumulative
Actual 103.22 3096.61
Prediction (s.d.) 91.52 (3.48) 2745.52 (104.37)
95% CI [84.63, 98.26] [2538.75, 2947.89]
Absolute effect (s.d.) 11.7 (3.48) 351.09 (104.37)
95% CI [4.96, 18.6] [148.72, 557.85]
Relative effect (s.d.) 12.79% (3.8%) 12.79% (3.8%)
95% CI [5.42%, 20.32%] [5.42%, 20.32%]
Posterior tail-area probability p: 0.0
Posterior prob. of a causal effect: 99.9%
For more details run the command: print(impact.summary('report'))
和
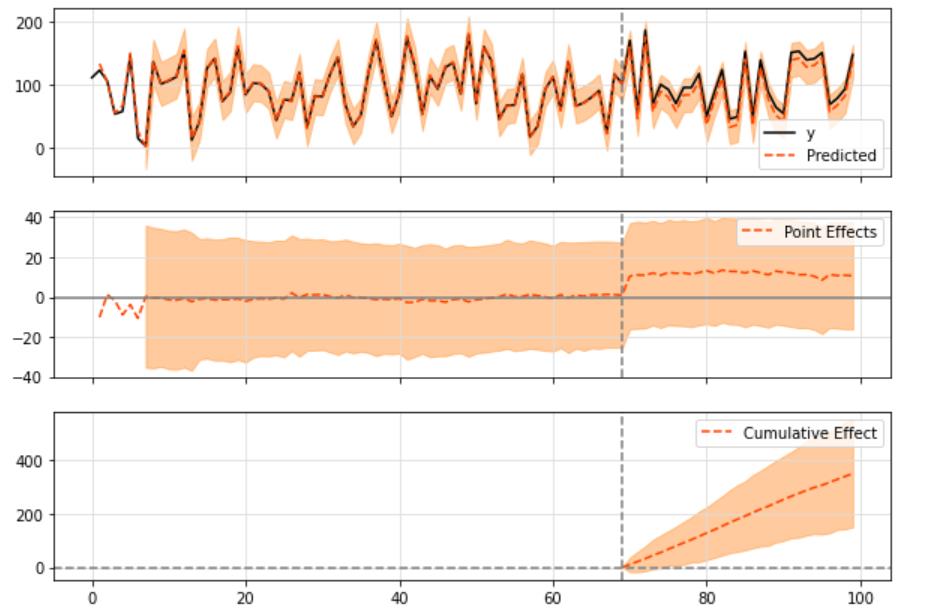
3.3.3 按时间进行筛选构造训练集
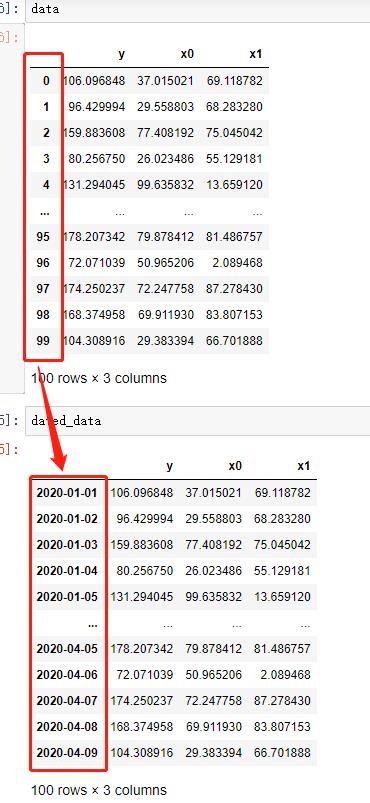
可以设定index为时间,就可以按照时间筛选pre / post时序数据:
dated_data = data.set_index(pd.date_range(start='20200101', periods=len(data)))
pre_period = ['20200101', '20200311']
post_period = ['20200312', '20200409']
figsize = (20, 6)
ci = CausalImpact(dated_data, pre_period, post_period)
ci.plot(figsize=(15, 14))
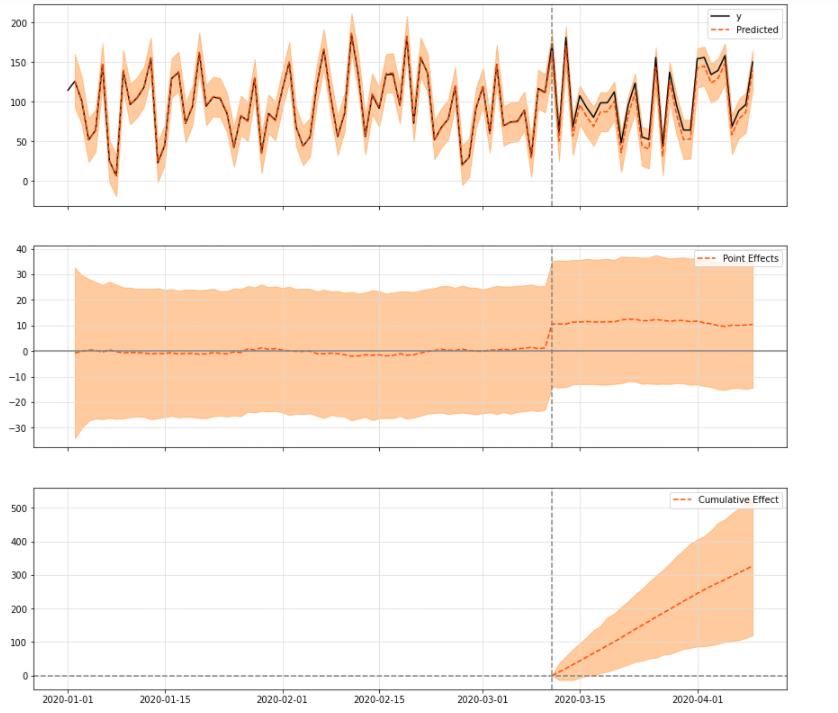
3.4 定制时序模型:线性回归做预测
就像在谷歌r包中一样,您也可以在这里选择一个定制的模型,在干预前阶段进行训练。
需要注意的是,如果希望数据标准化,那你给模型的数据就需要标准化了。
此外,模型必须使用dtype 32字节的数据(np.float32或tf.float32),否则,当运行TensorFlow时,它可能无法工作):
from causalimpact.misc import standardize
normed_data, _ = standardize(data.astype(np.float32))
obs_data = normed_data.iloc[:70, 0]
linear_level = tfp.sts.LocalLinearTrend(observed_time_series=obs_data)
linear_reg = tfp.sts.LinearRegression(design_matrix=normed_data.iloc[:, 1:].values.reshape(-1, normed_data.shape[1] -1))
model = tfp.sts.Sum([linear_level, linear_reg], observed_time_series=obs_data)
pre_period = [0, 69]
post_period = [70, 99]
ci = CausalImpact(data, pre_period, post_period, model=model)
ci.plot(figsize=(15, 12))
print(ci.summary())
3.5 Tensorflow_Probability 时间序列分解
gdata = pd.read_csv('../tests/fixtures/google_data.csv', index_col='date')
pre_period = ['2020-01-01', '2020-03-01']
post_period = ['2020-03-02', '2020-03-31']
ci = CausalImpact(gdata, pre_period, post_period)
print('Mean value of noise observation std: ', ci.model_samples['observation_noise_scale'].numpy().mean())
print('Mean value of level std: ', ci.model_samples['LocalLevel/_level_scale'].numpy().mean())
print('Mean value of linear regression x0, x1: ', ci.model_samples['SparseLine以上是关于跟着开源项目学因果推断——CausalImpact 贝叶斯结构时间序列模型(二十一)的主要内容,如果未能解决你的问题,请参考以下文章