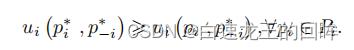激励机制中的经济学和博弈论模型

Posted 2023-03-31 白速龙王的回眸

论文标题：Incentive Mechanisms for Federated Learning: From Economic and Game Theoretic Perspective

分类图

总体而言，分类如下：
博弈论激励：非合作游戏、stackelberg游戏、联盟游戏
拍卖激励：盲拍、前向、倒向、双拍、组合拍卖
合同理论
匹配理论

博弈论

博弈论可以为多参与者交互决策建模，其中一个参与方的决定会潜在影响另一个参与方的。在FL的背景下，参与方可以市MO和DO，我们下面简要介绍一下博弈论的激励机制，然后它们有一些可以很好的奖励FL的参与方。一些术语：

玩家：决策者，可以选择它的动作，它们会倾向让自己的收益最大化
收益：表示玩家从游戏中赚或亏的钱
策略：是一套完整的动作计划，为了到达理想的结果。这个payoff取决于多个玩家的actions
平衡：每个玩家都可以达到它们认为的最大收益，如果它们要改变策略的话它们不会有任何收益，反应了博弈的稳定性

1）非合作博弈：每个player都是自私的，只关心自己收益的最大化，不关心FL系统的整体福利。players之间是不会合作的。我们考虑FL市场中的定价作为例子。DO（卖家）可以为提供的计算资源设置价格给MO（买家）。非合作游戏可以定义为三元组G = （Pi，ui，i belongs to N）这里N表示有N个卖家，Pi是i的卖出价格，ui是对于i来说，所有玩家固定策略时的收益。

我们有如下定义：
DEF1：假设pi是玩家i的最优策略，那么（pi,…,pn*)就是一个纳什均衡，意味着没有玩家可以通过改变当前策略（其他玩家不改变）的时候提高自己的收益，用式子表示就是：

这个式子表明，纳什均衡是这个游戏的稳定结果，因为卖家如果改变它们的策略并不会获得收益（单方面）。
然而，在一个游戏里面，可能会不存在NE或者存在多个NE，这就让palyer很难预测游戏的结果。因此在非合作游戏中，我们要验证NE的存在唯一性。有定理表明，唯一的NE存在当且仅当每一个player的策略空间是凸集（非空，闭集，有界）且收益函数是连续且类凹函数。

非合作博弈假设信息作为特征，player的收益函数和策略是公开的，这个就是一个完全信息游戏。然而，在实际当中，一个player可能不会太注意到其他palyer的信息，可能只知道每种类型出现的概率，这种就叫做不完全信息博弈。在FL市场中，关于DO可靠性和信誉的先验知识可以帮助分配奖励的，这些知识MO可能不知道。一个典型例子就是贝叶斯博弈，游戏的结果可以通过贝叶斯分析来预测。这个的均衡就是BNE，类似完全信息博弈的NE，当每一个player选择一个策略取最优化它们的期待收益（利用它们对其他player类型和策略的估计），BNE可以被计算出来。因为非合作博弈构建了自私players之间的冲突，FL市场中DO是竞争的然后MO的钱是有限的都可以构建为非合作博弈。这个对应的NE匀速DO有一个最优的参与策略。在FL中，这可以利用有竞争力的预测服务提供者进行计算资源交易。

2）Stackbelberg Game：
Stackelberg博弈是一个随着时序移动的博弈，在这里面，player作为leader的首先移动，然后其他player作为follwers的在观察了leader的移动之后再移动。因此，它也叫做leader-follower博弈。这个博弈的目标是建模一个多agent的决策过程，然后最大化在给定leader策略下的leader和follower的最大收益。

重新考虑一下我们有两个player，也就是计算资源的销售方。P1和P2表示两个player各自的策略。1和2都希望最大化它们的效用ui(p1,p2)。假设player 1在阶段1选择了它的策略，因此它就是一个leader。player2在阶段2选择了策略，所以他就是follower。这个关于leader和follower的共同优化问题就是Stackelberg游戏，它们的解构成了SE

DEF2：假设p1和p2分别是leader和follower的最优策略，那么(p1*,p2*)是SE当且仅当对于任意的(p1,p2)
我们有

通常来说，反向推理方法经常用于求解SE。在上述的例子中，给定p1，首先我们可以让follower求解出p2*，然后对于leader而言，我们用p2替换掉p2就可以求解出p1。因为player1知道paler2知道p1作为优势，player1会强加一个对自身有利的solution。
因此，在SE中，leader的效用总是高于follwer的，这个就叫做第一个移动者的优势。对应地，当到达了SE之后，leader可以获得至少和对应NE相当地收益。这个特征使得Stakelberg博弈适合FL的激励机制的设计。例如，它可以允许followers在知道leader（MO）对CPU资源的需求或者奖励的发放后，再来决定计算资源的定价

3）联盟博弈：在合作游戏中，player之间互相合作来使得整个联盟的共同目标最优化。进一步来说，player之间签订了强制性的条款。在这情况下，palyer可以协调策略然后达成一个关于怎么分配总收益给联盟中的player的共识。联盟博弈的目标是为了寻找一个稳定的解可以保证博弈的结果是免疫于player的变更的

拍卖

拍卖是一种经济的机制，它的目的就是分配商品（例如训练数据，计算资源和带宽等），然后建立一个对应的价格通过一个叫“竞价”的过程。一个拍卖包括一个精确的规则集合，这些规则通过市场参与者的基础来决定资源的分配和价格。拍卖中有术语如下：

竞价方：竞价方就是买方，它们希望在拍卖中购买物品。在FL中，买房可能是MO或者是FL需求方
卖方：卖方给卖方提供服务或资源。在FL中，卖方通常是DO或者那些使用本地数据训练共享模型的客户
拍卖中间商：中介，决定价格和获胜方。很多情况下，卖方也担任中介。
价格：可能是asking price或者bidding price。asking price就是seller希望获得的price，然后bidding price就是buyer希望支付的price。Hammer price就是最终拍板的价格。
商品：买方和卖方要交易的东西，它对应着buyer和seller想买的价格和想卖的价格。在FL中，商品可以是一个数据单元（训练数据样例）或者是一个计算资源单元（do提供的）
价值：在拍卖中，价值就是值商品值多少钱。不同的买卖方会根据自己的偏好得到不同的价值。每个参与者心中的价值可以是私有的也可以是公开的。
效用：买方的效用是不同于商品的价值和最终的支付的。卖方的效用，也就是收益，指的是它从buyer那里获得的总支付。在FL中，buyer的效用，例如MO，可以是正比于全局模型的精确度以及反比于给DO的总支付
社会福利：指的是每个user（buyer + seller）的总效用

拍卖机制被广泛地应用在多个领域，例如无线系统地资源分配，安全数据下载，网络安全。接下来，我们介绍在FL中常用的拍卖类型

1）盲拍：不同于公开拍卖，在盲拍中，buyer提交一个隐藏的竞价给中介。对应的，没有bidder知道别人的bidding价格，也不能更换自己的价格。下面是三种类型的拍卖：

• First-price 盲拍：谁bid的钱最多谁就是赢家，然后可以获得item
• Second-price 盲拍（Vickrey）：第二高bid的玩家才是赢家。因为胜者支付的价格比它期待的要少，所以这个协议促使buyer真实的拍卖，因此拍卖很可信。这个特征使得**这个拍卖策略在FL中常被使用，用来防止不可信节点的恶意行为
• Vickrey-Clarke-Groves拍卖（VCG)：是一个冠以的Vickrey拍卖（适用于多个商品）。在VCG里面，商品根据社会最优的行为来分配，然后胜者支付由于赢了商品造成的社会价值的丢失。这种支付规则使得bidder会根据商品之际价值正常的叫价。因此，VCG是一个可信的机制。在FL中，VCG机制可以用来激励DO来报告它们关于网络操作的真实价值，从而来最大化社会的福利。

2）前向拍卖，反向拍卖，二次拍卖：

• 前向拍卖：多个buyer先提交bids，然后对于一个seller来说看看谁的叫价高
• 反向拍卖：多个seller先提交asks，然后对于一个buyer来说看看谁能接受。一般来说，反向拍卖都和盲拍结合之类的。
• 二次拍卖：在FL中，存在多个MO和DO，二次拍卖可以用来匹配供给和需求。在二次拍卖中，buyer和seller同时提供它们的bids和asks，给一个中介。中介会决定一个price p，就是交易费，为了清空市场，一般来说asks < p and bids > p。一般来说p = (pb + ps) / 2,pb是bids，ps是asks。买方接受资源，卖方获得交易费。（那消失的(pb - ps) / 2是不是被中介吞了？）这个过程一直重复，直到没有新的交易出现或者到达预计的结束时间

3）组合拍卖：在组合拍卖中，buyer的每一个bid都意味着一大串的商品。基于bid中的信息和seller中的商品容量，中介可以决定最优的分配策略和获胜者。然而，解决winner对于组合拍卖是NP难问题，没有多项式解法来找到最优的分配。这里有很多算法来得到问题的近似解，例如拉格朗日估值。在FL中，组合拍卖用来分配网络操作者的带宽来掌控FL SP（service provider）

合同和匹配理论

合同和匹配理论被认为是建模关于不同类型的明知且自利的player动态和互相利益关系的两大杀器。特别地，它们可以有效地解决交易市场的高动态性，以及自利和竞争的player。下面，我们简单介绍合同和匹配理论以及FL的设计

1）合同理论：合同理论是一个经济的理论，他认为每个交易和机构都是一种合同。他在雇佣者和雇佣人的非对称信息里面经常使用（也就是说，员工的未来老板是不准确知道的）。在FL里面，因为打工仔都是自私的然后它们可能不会暴露它们的真实bids以及它们在FL中的隐私保护性质，因此存在着信息不对称。合同理论可以设计一个最优的合同来减少道德威胁，不利的选举，以及在信息不对称中的派系扭曲这个特征使得合同理论可以使用于FL中的激励机制的设计。在FL背景下，一个老板可以是一个MO它希望雇佣worker来完成FL的模型训练。同样的，一个员工（do），希望加入到FL中。一个三维的合同激励机制同时考虑任务的支出和隐私问题在70中被提出。一个两阶段的基于动态合同的激励机制在71提出，来激励不同意愿的user来参加。基于个人隐私保护的合同激励72可以提供对不同隐私偏好的worker进行传统的支付（ps：这就是激励+ 隐私嘛？？！！）

2）匹配理论：匹配理论的目标是最优化匹配两个不相交的agent集合（给定它们每个个体的效用下）。在通常的分配博弈模型，可能会有多个agents在matching的两端出现，然后一边的agents会和另一边的agents进行交易。因此，这种游戏叫做双边匹配。在匹配理论中，agents之间互相竞争，从而最大化它们的效用（自私程度），然后总是做那些可以增大它们效用的决定（贪心，理智）。**在FL中，这个被用来进行任务的分配，目标就是最小化系统的延迟（在多任务FL的场景下）

总结

这节介绍了经济学和博弈论模型的知识，然后提出它在FL的应用。具体的，我们介绍了定义，机制描述，合理性分析等。

经济学中的人性抉择（下）

序

上一篇分享了公地悲剧、逆向选择和道德风险三类资源无效配置的场景，在这三种场景下，信息不对称助长了“歪风邪气”。

这一篇我们将引入博弈论的基础知识，通过一个简单的模型来重新审视“信息对称”的重要作用，也重新来认识人性的“自私”。

先简单介绍一下博弈论：

博弈论，英文原文为 game theory ，也就是游戏策略。它需要2个或2个以上的参与者，每个参与者都拥有一定量的信息，并能够选择自己的策略，以争夺某种稀缺的资源或收益。

可以看到，博弈论实质上是生活中诸多场景的简化模拟。

先来介绍一个最基础的博弈场景——囚徒困境。

---

囚徒困境

囚徒困境是一个典型的博弈策略，我们通过一个故事来描述它：

故事的主角是小明和小强，他俩因为从小不好好学习，长大以后没有收入来源，只好合伙入室盗窃为生，结果第一次作案就被警方逮个正着
因为警方怀疑他们作案，但并没有掌握确凿的证据，所以对他俩进行隔离关押、隔离审讯。警方告知他们：如果其中一方供认盗窃之事，则坦白从宽减刑2年，只需要判刑1年，而拒不供认的一方则加以妨碍公务罪加刑两年，共判刑5年；如果两方都供认偷窃之事，则都判刑3年；如果两方都拒不供认，则只能以私入民宅判刑1年。

站在局外人的角度考虑，双方只要都拒不供认，则会得到最好的结果——小明将会无罪释放，回家和小红过日子，小强还可以天天去健身房。假设两人可以沟通协定，或是都是“重义之人”，则他们将能够得到这个结果。但作为“理性”的“局中人”，他们不会选择这种策略。

作为小明来思考：如果小强够“义气”，不供认，在此条件下，自己供认则需要判1年，自己不供认也要判1年；如果小强选择了供认，那么在此条件下，自己供认需要判3年，自己不供认需要判5年。因此，无论在哪种条件下，自己选择供认都是占优策略。
同样作为小强，也面临着同样的选择，图表如下：

强\明	抵赖	招供
抵赖	1  1	5  1
招供	1  5	3  3

从图表中也可以直观的看出，两人的优势策略都是招供，但整体上确是最无效的选择。这种无效性是由于每个人都不知道对方最终的选择，即只具有局部信息，以至于合作无法进行，个人只能在对方选择特定策略的条件下来选择自己的占优策略，这种最终必然被选定的策略可以称作均衡策略，也可以叫做纳什均衡。

---

官场中的囚徒

我们常常感觉到官场是一个染缸，圣人进去，出来也成了墨色。这又是为什么？同样先来看一个故事：

玉戭（yǎn）生和三乌丛臣是朋友。玉戭生说：“我辈应该自我激励，他日入朝（为官），权势人的门绝不涉足。”三乌丛臣说：“这是我痛恨得咬牙烂心的行为，干吗不对这事发个誓？”玉戭生很高兴，就歃血盟誓道：“二人同心，不徇私利，不为权位所诱，不趋附奸邪献媚的人而改变自己的行为（准则）。如有违背此盟誓，神明杀死他。”
没多久，他们一起在晋国为官。玉戭生重申以前的誓言，三乌丛臣说：“说过的誓言犹如还在耳畔，怎么敢忘记啊！”当时赵宣子在国王前得宠，各位大夫每天奔走于他家。三乌丛臣反悔（当初的誓言），又怕玉戭生知道他反悔，又不能不去（赵宣子家）。鸡一报晓，就前去 侍侯宣子。进得门来，见在正屋前东边的走廊有个端正地坐在那里的人，举灯一照，是玉戭生。各自羞惭退去。

在这个故事中，两人最终都背叛了誓言，选择了巴结权贵，这个模型的图表如下：

玉\三乌	巴结权贵	不巴结
巴结权贵	升官  升官	升官  落选
不巴结	落选  升官	落选  落选

从图表中可以看出，无论其他人怎么做，自己选择巴结权贵都是占优策略，也就是说，官场上的策略均衡点落在了“巴结权贵”上。因此，在古往今来的所有官场之中，趋炎附势、贪污腐败从来都是常态。

---

比比皆是的囚徒困境

除了官场之外，囚徒困境的例子在生活中比比皆是，以下举几个常见的例子：

1.职工权益：职员在要求提高福利或拒绝加班时面临典型的囚徒困境。如果所有职员都拒绝加班，那么每个人的收益可能是1；但倘若其中有一个人不拒绝加班，则势必会得到老板的青睐，从而收益可能是5；当每个人都选择加班时，老板就不会只青睐某个人，所有人的收益都变成了-1；如果其他人都选择加班，而某个人拒绝加班，则有可能被穿小鞋或借故辞退，他的收益为-5。那么，策略表如下：

个人\其他人	加班	不加班
加班	-1  -1	5  1
不加班	-5  -1	1  1

从表中我们可以看出，无论其他人选择加班或是不加班，个人选择加班的收益都更大，所以最终的纳什均衡点落在了（加班、加班）上，从而每个员工都只能选择加班。

2.消费者权益：与职工权益类似，团体消费者（比如购买同一个小区住房的业主）在维权时，也存在着同样的囚徒困境，因而所有人都愿意选择等待其他人维权最终自己享受同样的成果。这种做法最终的结果就是维权难以成功，总是便宜了商家。

3.学生时代在操场长跑时涌现的各路bitch，“曾经说好了一起跑，可你却偷偷加了速”。实际上，在跑步之前约定一起慢慢跑就是在制造一个虚假的“共识”，从而形成一个囚徒困境，这时选择背叛的人就能够获得最大的利益。

4.势均力敌的公司之间所进行的价格战：无论对方是否降价，自己降价都是占优策略，均衡点在“双方都降价”。

5.国家之间的关税战：无论别国是否提高关税，自己提高关税都是占优策略，均衡点在“双方都提高关税”。

6.恋爱：无论对方是否付出，为你付出多少，自己选择不付出都是占优策略，均衡点在“双方都不付出”，所以这也是现在谈恋爱走心越来越困难的愿意之一。

7.不忠：无论对方是否对自己忠诚，自己不忠都是占优策略，均衡点即是“双方都不忠”，所以婚姻很难保鲜啊。。。

虽然上面列举了如此多的囚徒困境，均衡点都很阴暗，似乎囚徒困境的均衡点总是“背叛”，以至于让笔者对人生产生了些许绝望之情，，但是尽管如此，社会并没有完全发展到这样负面的境地，为什么？

最后一个小节我们将用来回答这个问题。

---

囚徒困境的结果为什么并不一定落在均衡策略上？

其中一个原因是人类并非“完全理性”，感性、感情等在决策中占据了一席之地；另一个更重要的原因在于，道德和法律制度的约束改变了矩阵中的收益，从而改变了均衡点。

举个例子，选择对伴侣不忠的人尽管享有了多个伴侣带来的收益，但同时也受到道德的强烈谴责，选择离婚还会失去财产，而重婚则是犯罪行为，，如果一个人足够的重视道德品质或重视财产，那么选择不忠可能就不是一个占优策略，这时的纳什均衡点就落在了“忠诚，忠诚”上。见下表：

对伴侣不忠，而且没有其他外在约束时可能的矩阵收益：

自己\伴侣	忠诚	不忠
忠诚	3  3	-5  5
不忠	5  -5	-3  -3

上述矩阵我们可以理解为，两人都忠诚时，爱情的收益为3；两人都不忠诚时，失去爱情的收益为-3；而当自己忠诚伴侣却不忠诚时，自己不仅需要承担失去爱情的-3，还会产生被欺骗等负面的情绪-2；反之如果自己不忠而伴侣忠诚，则不仅自己享有爱情的收益3，还享有“出轨”的收益2。最终我们发现，无论伴侣是否忠诚，自己选择不忠都是占优策略，所以纳什均衡点落在“不忠，不忠”上。

但如果有其他约束存在，比如选择忠诚可以得到更多的美誉+1，而选择不忠则会身败名裂-2，这时矩阵的收益变化如下：

自己\伴侣	忠诚	不忠
忠诚	3+1  3+1	-5+1  5-2
不忠	5-2  -5+1	-3-2  -3-2

整理如下：

自己\伴侣	忠诚	不忠
忠诚	4  4	-4  3
不忠	3  -4	-5  -5

我们可以看到，此时无论伴侣是否忠诚，自己选择忠诚都是占优策略，因此纳什均衡点又落在了“忠诚，忠诚”上。

但是，一旦外部条件发生变化，纳什均衡点就会再次发生变化，常见的，比如新遇到的“外遇对象”颜值足够高，那么选择“不忠”的收益将扩大，均衡点可能会回落到“不忠，不忠”上。

在上面的例子中，实质上结果始终是落在均衡策略上的，只不过加入了新条件的困境实际上已经不是原来的那个困境了，所以看起来好像是结果发生了变化，实际上只是条件发生了变化而已。

囚徒困境的结果不一定落在均衡策略上，还有第三个最重要的原因——多次博弈。

你是否注意观察过，火车站附近的小饭店做的饭常常十分难吃，而你们家附近的小饭馆做的饭却比较可口且实惠？

在博弈论中这一点非常好解释，因为火车站附近的小饭馆顾客们基本只会来一次，所以偷工减料不用心做将带来更多的收益，我们看下图——火车站附近小饭店的收益矩阵：

饭店\顾客	仅一次
好吃	1  3
难吃	3  1

这个矩阵不是标准的囚徒困境矩阵。在这里我们只需要理解核心部分，因为顾客只来一次，所以饭店采取“难吃”的策略将会获得更多的收益。

但在家附近的小饭馆，如果做的不好吃，下一次就不会再来吃了，

饭店\顾客	第一次	第二次	第三次	第n次
好吃	1  3	1  3	1  3	1  3
难吃	3  1	0  0	0  0	0  0

观察矩阵我们可以看到，店家做的难吃将会断送以后所有的收益机会，因此店家的占优策略就是做的好吃。

类似的，在第一节中描述的两个囚徒，如果需要做多次博弈，他们必然会在不断的博弈中从背叛走向合作，因为尽管信息无法共享，但每个人都知道，如果自己选择合作赢取对方的信任，那么在下一次的博弈中，对方也会选择合作（如果对方依然选择背叛，自己也可以通过背叛来惩罚他，多次之后双方必然共同选择合作）

在关税问题上的囚徒困境问题就是通过多次博弈来调节的。因为A国增加关税必然引起B国同时增加关税，而这样会对A国也造成不利影响，多次博弈之后两国必然遵守契约同时降低关税。

类似上述的情景在生活中还有很多，比如人们在认识的人中更愿意展现自己优秀的一面，更谦让，而对不认识的人可能会不讲礼貌；又比如人们在生活中可能竭力扮演一个谦和、听话、认真、乐于助人的角色，而在网络上却变得肆无忌惮。

在上一篇中我们说到逆向选择问题，实际上二手车市场也可以看作一个囚徒困境，因为无论车子好不好买家支付更低的价格都是占优策略，因此，拥有好车的卖家只好退出市场。而且二手车交易基本是单次博弈，所以不存在多次博弈的调节机制。

---

结束语

博弈论是一门宏大的学问，但却不是一门完备的学问。借助这个工具，我们能更好的探索世界，也能更好的了解人性，但它并不是对这个世界最好的描述——最好的描述可能只是世界本身。

囚徒困境产生的其中一个条件是局中人面临不完备的信息。这种信息的不对称性，其一在于信息的获取往往是不对称的，可能是由于成本过高或是其他原因导致的信息闭塞；其二在于人们相互之间的不信任，即便某人说出了自己会采取的策略，别人也无法断定他将会按照自己所说的策略行事（即可能存在欺骗）。

因此，在这个世界上，想要减少类似的困境，真正实现集体资源的有效配置，实现集体价值和个体价值的统一，可能是比探索宇宙起源更难的事情，我们要做的还有很多。

愿天下大同，再无纷争，愿人类相互理解的时代终有一天能够到来。