PCL 计算空间三角形的面积
Posted 点云侠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PCL 计算空间三角形的面积相关的知识,希望对你有一定的参考价值。
目录
一、算法原理
1、空间三角形面积
空间三角形面积的计算公式为:
A = P ( P − S 1 ) ( P − S
PCL:getCircumcircleRadius ❤️ 计算三角形外接圆半径
文章目录
1 外接圆半径公式
经过三角形各顶点的圆叫做三角形的外接圆,表示三角形外接圆半径的方法有:
- 用三角形的边和角来表示它的外接圆的半径;
- 用三角形的三边来表示它的外接圆的半径;
- 用三角形的三边和面积表示外接圆半径的公式。
1.1 用三角形的边和角来表示它的外接圆的半径
设在
△
A
B
C
\\triangle ABC
△ABC 中,已知一边和它的对角,由正弦定理的推论知,外接圆的半径
R
R
R 可由已知边和角来表示:
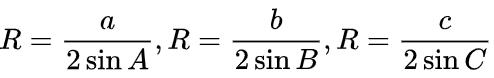
1.2 用三角形的三边来表示它的外接圆的半径
设在
△
A
B
C
\\triangle ABC
△ABC 中,已知三边
a
,
b
,
c
a,b,c
a,b,c,则
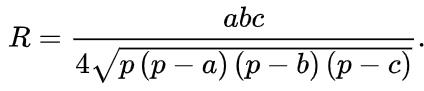
其中,
p
=
a
+
b
+
c
2
p=\\cfrac{a+b+c}{2}
p=2a+b+c
1.3 用三角形的三边和面积表示外接圆半径的公式
R
=
a
b
c
4
S
R=\\cfrac{abc}{4S}
R=4Sabc
其中,
a
,
b
,
c
a,b,c
a,b,c 为三边边长,
S
S
S 为三角形面积
本文就是用这种方法计算三角形外接圆半径
2 函数原型
pcl::getCircumcircleRadius (const PointT &pa, const PointT &pb, const PointT &pc)
3 代码实现
给定三角形的三个顶点,返回三角形外接圆半径。
#include <iostream>
#include <pcl\\io\\pcd_io.h>
#include <pcl\\common\\common.h>
using namespace std;
int main()
{
pcl::PointXYZ p1, p2, p3; //三角形的三个点
p1.x = 0;
p1.y = 0;
p1.z = 0;
p2.x = 10;
p2.y = 0;
p2.z = 0;
p3.x = 5;
p3.y = 10;
p3.z = 10;
float radius; //三角形外接圆半径
radius = pcl::getCircumcircleRadius(p1, p2, p3);
cout << "->三角形外接圆半径为:" << radius << endl;
return 0;
}
4 输出结果
->三角形外接圆半径为:7.95495
5 源码
template <typename PointT> inline double
pcl::getCircumcircleRadius (const PointT &pa, const PointT &pb, const PointT &pc)
{
Eigen::Vector4f p1 (pa.x, pa.y, pa.z, 0);
Eigen::Vector4f p2 (pb.x, pb.y, pb.z, 0);
Eigen::Vector4f p3 (pc.x, pc.y, pc.z, 0);
double p2p1 = (p2 - p1).norm (), p3p2 = (p3 - p2).norm (), p1p3 = (p1 - p3).norm ();
// Calculate the area of the triangle using Heron's formula
// (http://en.wikipedia.org/wiki/Heron's_formula)
double semiperimeter = (p2p1 + p3p2 + p1p3) / 2.0;
double area = sqrt (semiperimeter * (semiperimeter - p2p1) * (semiperimeter - p3p2) * (semiperimeter - p1p3));
// Compute the radius of the circumscribed circle
return ((p2p1 * p3p2 * p1p3) / (4.0 * area));
}
相关链接:
以上是关于PCL 计算空间三角形的面积的主要内容,如果未能解决你的问题,请参考以下文章