Super easy to understand decision trees (part one）
Posted Huterox
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Super easy to understand decision trees (part one）相关的知识，希望对你有一定的参考价值。
文章目录
- The preface
- What can it do
- how it work
- The data format
- Information entropy and GINI coefficient
- The Gini coefficient
- Code the decision tree algorithm
- summary
The preface
How Long so see gays,okey i don’t know what will be happen if i wriiten this papay by English but i want to try,hey~.
welcome to my channel for reading something about machine learnning. Today i will talk something about decision tree.
In this blog we have two target!
- What about decision tree and how it work.What’s the math involved?
- How to write a decision tree algorithm by Python
But in this blog i will just make a simple Decision Tree mode,so this is why i need add an explanation in blog title.
Okey ,let’s go!
What can it do
First decision trees can do a lot of things, such as the classification of the classic problems, as well as the continuous prediction problem, and most importantly, the implementation of a decision tree algorithm, only need to know about the most basic information entropy principle can write a decision tree algorithm, and this is also why I choose this algorithm first, Because it’s the simplest and easiest to understand for us just like linear regression.
such as i give you a table which has some data in and then i will give you some new data without in that table hoping you can forcast the result.
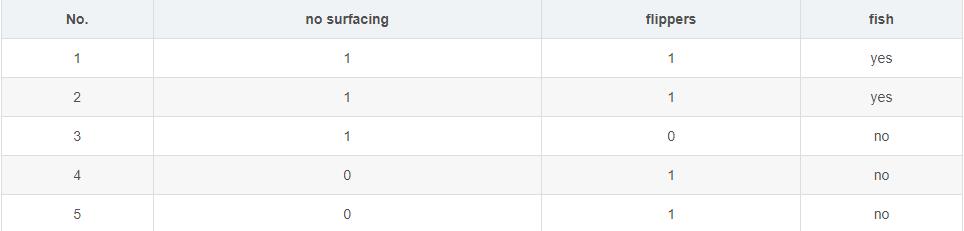
how it work
Before we how it.we should to know “In the past many years, machine learning has been divided into many schools, among which machine learning theory based on statistical mathematics is widely used in today’, and decision tree is definitely a very classical representative algorithm.” so it working principle just like you play many games to guess what will be happend next time in you game,for that you should to play enough times to find some rules and this is the core in today’s algorithm.You use a great deal of experience in playing games to determine what your current state is in order to make a decision.
But the machine can’t thinking like us, it means we must input accurate data and define a funcation when it running and then we can get some return.So for fishing these wrok we need use mathematical statistics.
The data format
This is very important for us to lean a new machine algorithm,because it involve what we will do in our algorithm.
So let’s take a closer look at the picture above, although you might see at a glance what it means
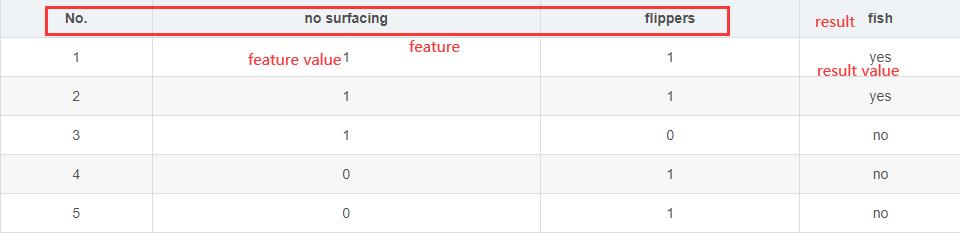
When you want to find some rules,i think you must will be find by feature,and then forcast your result by feature value.So the most imporant is that what feature can easy to show some relation in these data and how use these feature to help us make forcast. The decision tree is great idea,such as this:
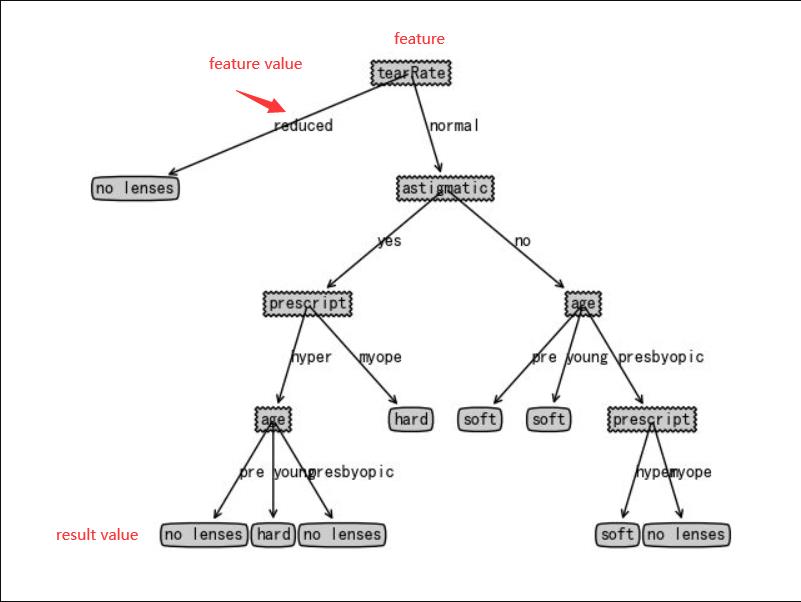
Okey,now we know we can use decision to help us to find some relationship(you can also use neural networks),but how to determine the location relationship of decision trees as features, the execution process becomes another problem we need to solve.
Information entropy and GINI coefficient
Entropy is an important concept in statistics. It is used to select features and measure the uncertainty of results. The smaller the information entropy, the more uniform the results. And our goal is really to try to find a relationship that will allow us to get closer to some kind of unity in our classification, in our prediction.Therefore, we can use entropy as a basis for determining the shape of the decision tree.
Information entropy
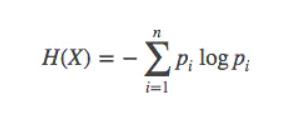
Conditional entropy:
When a feature is fixed, the uncertainty of the result is the conditional entropy:
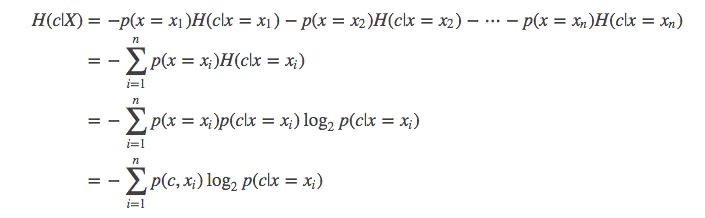
With this, when selecting nodes in the decision tree, we can calculate the conditional entropy of each feature on the resulting value and choose the smallest one.
Information gain
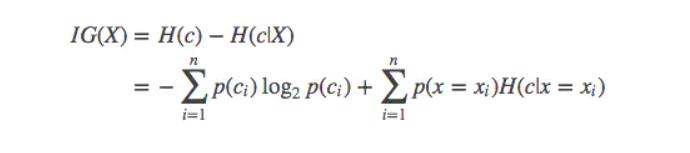
The original entropy - conditional entropy is the stability gain of the system brought by this determined variable
Information gain ratio
A big problem of information gain is that the attributes with more branches are preferred to be overfitting, and the information gain is punished by fitting more values than the formula (pruning is necessary anyway).
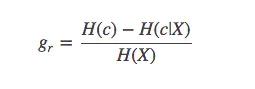
The Gini coefficient
In CART, Gini coefficient is used to construct binary decision tree. In binary classification problem, it is approximately half of entropy, but the calculation is simpler:
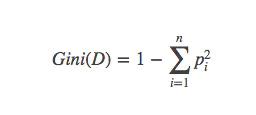
And similar Gini gain and gain rate are similar to the entropy above
Code the decision tree algorithm
Well, with some basic principles in mind, it’s time to start our coding work
Algorithm process
To write our algorithm, we need to determine the specific algorithm process, which is roughly as follows:
1. Calculate the entropy of the original result
2. The entropy/GINi gain ratio of each feature to the result is calculated, and the node with the largest gain ratio is selected as
the current node
3. Determine the branch of the current node, the calculated value of the current as the characteristic of node, as a kind of situation (in
the performance of the decision tree as the branches of the tree) to
calculate the corresponding conditional entropy (can determine whether
the entropy between 0, if zero current branch no longer generate a new
node, instead need to access the new node) behind
4. Call recursively until the build is complete
Don’t worry, we’ll do it in code:
def BulidTree(self,dataSet:list, labels:list)->dict:
resClass = [sample[-1] for sample in dataSet]
if (resClass.count(resClass[0]) == len(resClass)):
return resClass[0]
if (len(dataSet[0]) == 1):
return self.__majorityCnt(resClass)
bestFeature, index = self.__chooseBestFeatureToSplit(dataSet, labels)
myTree = bestFeature:
del labels[index]
# divide branch
featValus = set(sample[index] for sample in dataSet)
for value in featValus:
sublabels = labels[:]
myTree[bestFeature][value] = self.BulidTree(self.splitDataSet(dataSet, index, value), sublabels)
return myTree
(We can tell if entropy is 0 by seeing if all the values in the result set are the same)
The representation of a tree
Okey,the next problem is how to representation a tree in machine?Now will code by python.So the easiest thing to think of is to use Python’s dictionary data structure.
such as:
Select the node
this code include how to caculate gini or entropy.
def __chooseBestFeatureToSplit(self,dataSet:list, index_labels:list)->(object,int):
numFeatures = len(dataSet[0]) - 1
baseEntorpy = self.__computeEntropy(dataSet)
bestInfoGainlv = 0
index = 0
for i in range(numFeatures):
featList = [feat[i] for feat in dataSet]
uniquvalues = set(featList)
newEntorpy = 0
for value in uniquvalues:
subDataSet = self.splitDataSet(dataSet, i, value)
prob = len(subDataSet) / (len(dataSet))
newEntorpy += prob * self.__computeEntropy(dataSet=subDataSet)
current_featEntropy = self.__computeEntropy_indexLabels(dataSet,i)
infoGainlv = (baseEntorpy - newEntorpy)/(current_featEntropy+1)
def __computeEntropy(self,dataSet:list)->float:
num = len(dataSet)
resultCounts =
for data in dataSet:
if (resultCounts.get(data[-1])):
resultCounts[data[-1]] += 1
else:
resultCounts[data[-1]] = 1
Entropy = 0.
if(self.mode=='gini'):
Entropy=1.0
for value in resultCounts.values():
prob = (value / num)
if (self.mode == "gini"):
Entropy -= (prob * prob)
else:
Entropy -= prob * (math.log2(prob))
return Entropy
def __computeEntropy_indexLabels(self,dataSet:list,index:int)->float:
num = len(dataSet)
labelsCounts =
for data in dataSet:
if(labelsCounts.get(data[index])):
labelsCounts[data[index]]+=1
else:
labelsCounts[data[index]] =1
Entropy = 0.
if(self.mode=='gini'):
Entropy=1.0
for value in labelsCounts.values():
prob = value/num
if(self.mode=="gini"):
Entropy-=(prob*prob)
else:
Entropy-=prob*(math.log2(prob))
return Entropy
It should be noted that we need to calculate two kinds of entropy /gini here, one is the feature on the result, and the other is the feature itself, in addition, the index_labels here is actually the feature names
To predict
This is pretty simple, just make a prediction, we just have to parse the structure of the tree
def forcast(self,Tree:dict,data:list):
node = list(Tree.keys())[0]
return self.__forcast_self(Tree,data,node)
def __forcast_self(self,Tree:dict,data:list,node=None):
if(not isinstance(Tree,dict)):
return Tree
index = self.index_labels.index(node)
key = data[index]
Tree_values = Tree.get(node).get(key)
if(isinstance(Tree_values,dict)):
return self.forcast(Tree_values,data)
else:
return Tree_values
The complete code
Here is our complete code, where we also have some methods for validation
import copy
import math
class TreeMode(object):
def __init__(self,dataSet,index_labels,mode="entropy"):
"""
suport tow mode entropy and gini
:param mode:
"""
self.dataSet = dataSet
self.index_labels = copy.deepcopy(index_labels)
self.mode = mode
def __majorityCnt(self,resClass:list):
# find majorityCnt number
count =
max_maj = 0
majority = None
for key in resClass:
if (count.get(key)):
count[key] += 1
else:
count[key] = 1
if (count[key] > max_maj):
max_maj = count[key]
majority = key
return majority
def __computeEntropy_indexLabels(self,dataSet:list,index:int)->float:
num = len(dataSet)
labelsCounts =
for data in dataSet:
if(labelsCounts.get(data[index])):
labelsCounts[data[index]]+=1
else:
labelsCounts[data[index]] =1
Entropy = 0.
if(self.mode=='gini'):
Entropy=1.0
for value in labelsCounts.values():
prob = value/num
if(self.mode=="gini"):
Entropy-=(prob*prob)
else:
Entropy-=prob*(math.log2(prob))
return Entropy
def __computeEntropy(self,dataSet:list)->float:
num = len(dataSet)
resultCounts =
for data in dataSet:
if (resultCounts.get(data[-1])):
resultCounts[data[-1]] += 1
else:
resultCounts[data[-1]] = 1
Entropy = 0.
if(self.mode=='gini'):
Entropy=1.0
for value in resultCounts.values():
prob = (value / num)
if (self.mode == "gini"):
Entropy -= (prob * prob)
else:
Entropy -= prob * (math.log2(prob))
return Entropy
def splitDataSet(self,dataSet:list, index:int, value:object)->list:
resDataSet = []
for data in dataSet:
if (data[index] == value):
reduceData = data[:index]
reduceData.extend(data[index + 1:])
resDataSet.append(reduceData)
return resDataSet
def __chooseBestFeatureToSplit(self,dataSet:list, index_labels:list)->(object,int):
numFeatures = len(dataSet[0]) - 1
baseEntorpy = self.__computeEntropy(dataSet)
bestInfoGainlv = 0
index = 0
for i in range(numFeatures):
featList = [feat[i] for feat in dataSet]
uniquvalues = set(featList)
newEntorpy = 0
for value in uniquvalues:
subDataSet = self.splitDataSet(dataSet, i, value)
prob = len(subDataSet) / (len(dataSet))
newEntorpy += prob * self.__computeEntropy(dataSet=subDataSet)
current_featEntropy = self.__computeEntropy_indexLabels(dataSet,i)
infoGainlv = (baseEntorpy - newEntorpy)/(current_featEntropy+1)
if (infoGainlv > bestInfoGainlv):
bestInfoGainlv = infoGainlv
index = i
return index_labels[index], index
def BulidTree(self,dataSet:list, labels:list)->dict:
resClass = [sample[-1] for sample in dataSet]
if (resClass.count(resClass[0]) == len(resClass)):
return resClass[0]
if (len(dataSet[0]) == 1):
return self.__majorityCnt(resClass)
bestFeature, index = self.__chooseBestFeatureToSplit(dataSet, labels)
myTree = bestFeature:
del labels[index]
# divide branch
featValus = set(sample[index] for sample in dataSet)
for value in featValus:
sublabels = labels[:]
myTree[bestFeature][value] = self.BulidTree(self.splitDataSet(dataSet, index, value), sublabels)
return myTree
def forcast(self,Tree:dict,data:list):
node = list(Tree.keys())[0]
return self.__forcast_self(Tree,data,node)
def __forcast_self(self,Tree:dict,data:list,node=None):
if(not isinstance(Tree,dict)):
return Tree
index = self.index_labels.index(node)
key = data[index]
Tree_values = Tree.get(node).get(key)
if(isinstance(Tree_values,dict)):
return self.forcast(Tree_values,data)
else:
return Tree_values
def evaluate_predication(self,Tree,eval_data:list):
count_right = 0
num = len(eval_data)
for data in eval_data:
data_ = data[:len(data)-1]
pred = self.forcast(Tree,data_)
if(pred==data[-1]):
count_right+=1
return count_right/num
if __name__ == '__main__':
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 0, 0, 0, 'no']
]
labels = ["A", "B", "C",以上是关于Super easy to understand decision trees (part one）的主要内容，如果未能解决你的问题，请参考以下文章
One example to understand SemFix: Program Repair via Semantic Analysis
Teaching Machines to Understand Us 让机器理解我们 之二 深度学习的历史
Teaching Machines to Understand Us 让机器理解我们 之三 自然语言学习及深度学习的信仰
[React] Understanding setState in componentDidMount to Measure Elements Without Transient UI State(代
性能优化Observability Tools C++: Beyond GDB and printf - Tools to Understand the Behavior... - 知识点目录