模型并行 | 大规模语言模型架构 Megatron

Posted 2023-03-31 幻方AI小编

随着AI模型的规模越来越大，分布式训练技术越来越被广泛使用。现行的分布式训练方法主要包含两个部分：数据并行（Data Parallel）和模型并行（Model Parallel）。数据并行是将模型完整拷贝到多张显卡中，对批次数据进行并行计算，适合规模小而数据多的训练场景；而模型并行适合超大规模参数的模型训练，将模型不同的部分分别加载到不同的显卡中，依次计算得出结果。

Megratron是NVIDIA提出的一种分布式训练大规模语言模型的架构，针对Transformer进行了专门的优化，主要采用的是模型并行的方案。这篇文章将描述幻方AI对于NVIDIA Megatron在萤火二号平台上运行的一些实验，以及与我们目前的方法的对比。 ​

模型：GPT

代码：GitHub - NVIDIA/Megatron-LM: Ongoing research training transformer models at scale

环境：幻方萤火二号，16个节点共128张A100（A100-40GB x128）

---

Megatron简介

Megatron是NVIDIA提出的一种由于分布式训练大规模语言模型的架构，针对Transformer进行了专门的优化（也就是大矩阵乘法）。

第一篇论文发表于2019年9月：Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism，主要提出了通过将矩阵分块提高并行度的方法。

第二篇论文发表于2021年4月：Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM，对于分布式中的一些重要的设计，如tensor parallel、pipeline parallel、micro batch size等进行了一些分析与讨论。同时提出了更加精细的pipeline结构与communication模式。

Megatron作者提供的性能结果如下：

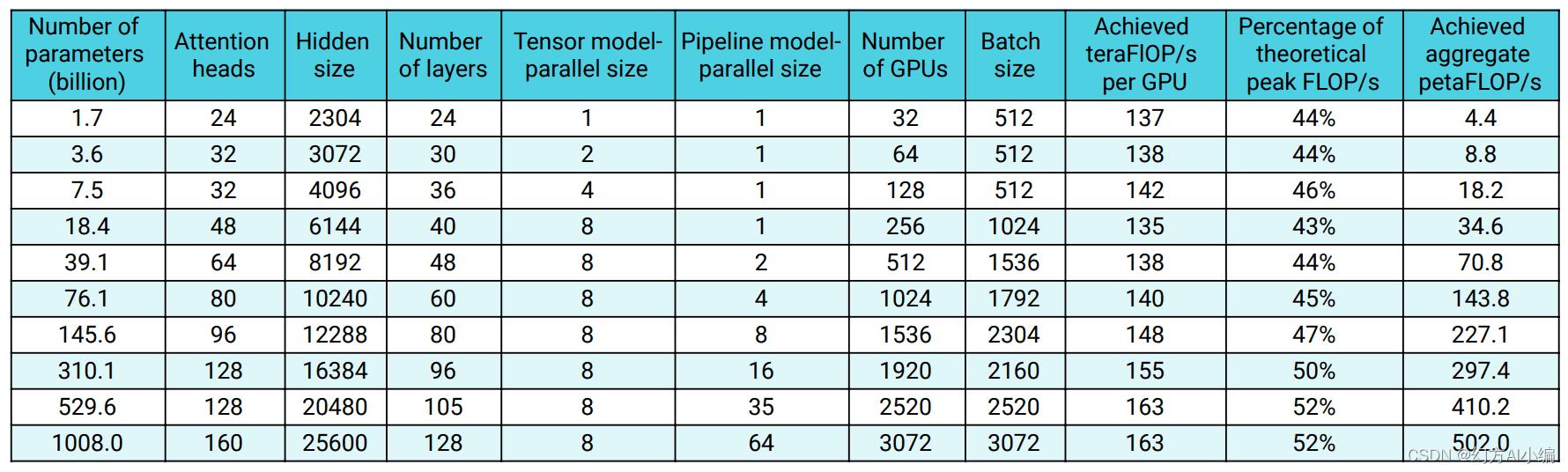
 这些测试是基于DGX A100-80GB集群完成的。和萤火二号的测试环境相比，硬件环境上主要存在着如下区别：

• DGX配备了NVLINK、NVSWITCH与IB，使得AllReduce的效率非常高。萤火二号的通讯效率相对更低，尤其是在不使用hfreduce的前提下。
• Megatron使用了A100-80GB而萤火二号使用了A100-40GB。除了显存大小不同之外，二者的内存带宽也不同（2.0T/s vs 1.6T/s）。

除此之外，除去实现细节上的差异，Megatron和我们的方法的主要不同在于

• Megaton支持tensor parallel，并相应地优化了数据传输。
• Megatron对于pipeline机制进行了一些优化（原论文Fig.4）。
• Megatron自行实现了一套DDP框架，而非使用pytorch提供的DDP。
• Megatron自行实现了一些fused kernels，但是为了公平对比被我们disable掉了。

我们关心的问题是，在萤火平台上，Megatron的架构能够达到怎样的训练效率。

我们用于测试的模型配置为：

• hidden size = 3072
• layers = 32
• attention heads = 32
• batch size = 512
• context size = 1024
• vocabulary size = 50264
• micro batch size = 4

总参数量为 3.8 B，单次迭代计算量为 16.53 PFLOP。

Tensor Parallel vs. Pipeline Parallel

在Megatron的论文中，作者的建议是在节点内尽量使用tensor-parallel。pipeline-parallel主要在节点间使用，目的在于增大可用显存，而且应当尽量少。这一观点的原因在于pipeline会不可避免地引入bubble而降低效率。然而，另一方面，tensor-parallel需要更多的AllReduce操作，不适合在带宽较低的设备之间进行。

在这一节中我们测试不同的tensor parallel与pipeline parallel的训练效率。我们的实验观察到了与论文结论相反的现象：

	TP = 1, PP = 4	TP = 2, PP = 2	TP = 4, PP = 1
time (s)	4.43	5.41	9.54
percentage of peak	9.4%	7.6%	4.3%

其中，TP = tensor parallel，PP = pipeline parallel。为了避免跨numa，每个进程使用4块GPU。更细致的log显示，无论是forward还是backward，在使用tensor parallel后的时间开销都显著增加。此外，GPU利用率远远低于论文中的结果（48%）。

为了排除数据传输的影响，我们在单卡上跑了一个小模型作为测试，单次迭代需要的计算量约为119.4 TFLOP，时间约为1950ms，那么也只有理论峰值的 19.6%。

Model Shape

第二个有趣的发现是，在总运算量一定的情况下，不同的（layers，hidden size）组合的计算效率会有较大的差别。

layer, hidden	20, 3872	32, 3072	52, 2400	80, 1920	80, 2048
PFLOP	16.4	16.5	16.5	16.5	18.6
Params (B)	3.99	3.94	3.84	3.74	4.24
Megatron (s/iter)	5.79	4.34	7.48	8.07	5.90
Ours (s/iter)	8.47	6.31	8.00	8.11	7.76
Megatron / Ours	68.4%	68.8%	93.5%	99.5%	76.0%

在一些特殊的形状下，（也就是GPU恰好效率不高的形状下），我们的方法和Megatron还是很接近的…在最优的形状下，差距还是很明显。猜测Megatron的论文里选用这个形状也是因为它的执行效率最高。背后的原因可能是某种尺寸的矩阵的GEMM效率最高。由此进一步推测，tensor parallel也能由于类似的原因实现优化。

Mixed Precision

Megatron默认是使用mixed precision（fp16）进行计算的。而且在前面的图里也能看到A100对于FP16的算力是TF32的两倍。我们做了一个简单的实验对比fp16与tf32在Megatron上的性能差异：

	FP16	TF32
s/iter	4.43	7.53

TF32的时间开销增加了约70%，这个结果是符合预期的。

但是：

1. 我们在过去的测试中，发现开关AMP并没有产生太大的性能差距
2. Megatron在TF32下的迭代时间与我们的方法有些接近

因此，一个怀疑是，尽管我们在代码中加入了torch.cuda.amp，它并没有真正生效，又或者是使用的方法并不是最恰当的。这可能是我们的方法和Megatron的性能差距的一个来源。当然，也有可能是Megatron完全使用了fp16（而不是mixed precision），这个问题还有待检查。

更新2022 Feb 17：经过检查代码，Megatron 的 —fp16 应该是启用了 mixed precision 的。在 optimizer.py 中可以看到对 fp32 参数的维护。

Pipeline Parallel vs DDP

 然而，另一个问题在于，当总GPU数量固定为n时，p 越小，data parallel的进程数 d=n/p 就越多。如果节点间的数据交换需要通过一个中心交换机的话，数据传输的效率可能成为一个问题。

在Megatron中，tensor parallel与pipeline parallel都是将大模型装进显存的方法。但前面的实验已经验证了，在萤火二号的平台上，需要大量带宽的tensor parallel并不合适。那么，理论上，只需要选取最小的 ppp 使得模型能够装入显存就可以了。

接下来是一个关于pipeline的简单实验。为了能够将模型装入单个GPU，我们将hidden size缩小到2048。

pipeline parallel	1	2	4	8	16
Megatron (s/iter)	2.84	3.25	3.19	3.01	3.40
Ours (s/iter)	OOM	2.80	4.40	7.69	not supported
Megatron / Ours		116%	72.5%	39.1%

对于Megatron来说，单卡是最快的，这个符合预期。然而，2卡反而是最慢的，8卡也并没有因为跨numa而显著变慢，16卡也没有因为跨node而显著变慢。作为对比，我们的方法随着pipeline parallel规模的增加，性能下降非常明显。猜测是因为Megatron的pipeline实现更加高效。

补充 2022 Feb 17：在上表中，Megatron 的 pipeline parallel 没有因为跨numa/node而显著性能下降是因为其显卡分配方式本来就是优先跨node的。即使当pipeline深度仅仅为2时，两块显卡也分布在不同的节点上。详见这份文档。

此外，我们的方法在单卡下会OOM而Megatron不会，可能是同样是因为我们没有正确地启用fp16，又或者是我们的实现有一些粗糙（考虑到我们只是调用torch，Megatron也是，按理说不该有很大差别）。

PyTorch自带的pipeline基于RPC实现，无法支持跨节点的pipeline。Megatron中的pipeline应该是作者自行实现的，还有待确认。

另外，上述关于pipeline的分析均基于一个假设：在pipeline的每一步，GPU都能够跑满。然而，实际情况可能并非如此。

先放张示意图：

 为了简单，只画了forward部分，backward本质上是一样的。现在假设每个GPU的算力没有跑满，所以它有两行。最上面的图表示一个常规的做法，分成3个micro batch。中间的图表示，如果GPU没有跑满的话，可以拆成6步流水线，每个GPU处理两步，那么效率会明显高于3步流水线。而最下面的图表示了另一种可能：尽管我们拆成了6步流水线，但是每一步都会把GPU跑满，体现为每个时间点GPU都只在处理一步运算。然而，在这种情况下，也并不会比拆成3步流水线的情况差。

由于Megatron的实现已经固定了每个GPU只能承载流水线中的一步，我们用我们自己的实现做个实验。

pipeline stages	4	8	16	32
forward	0.63	0.64	0.66	0.70
backward	4.53	4.19	3.83	3.59
total	5.50	5.11	4.74	4.53

可以看到，随着流水线变深，时间开销缩减到了原来的 83%。尽管foward小幅变慢，但是backward时间显著缩短。

需要指出的是，类似的提升 并不 总是能够在任何模型结构上都会发生。推测这是由于一些特殊的矩阵形状在GPU上的执行效率不高导致GPU没有跑满。上述结果来自于 layers = 54，hidden size = 1920，attention head = 20。这个实验仅仅提示在某些情况下，这样做可能带来加速。

在这些分析中，我们并没有考虑到pipeline带来的sync等overhead。但是从实验结果来看，这些开销是可以接受的。

实际上，我们真正应该减少的是pipeline所占用的GPU数量，而非总的流水线步骤。当我们观察到GPU并没有跑满的时候，在单个GPU内增加pipeline数量是有可能提高效率的：存在着某一个配置，能够平衡过多的pipeline数量带来的overhead与GPU利用率之间的关系。但是理论计算很难给出这个结果，因为overhead受到大量因素的影响。我们更可能需要经验性的实验去寻找这个平衡。显而易见的是，在节点，或者numa内部去分割pipeline的开销是注定远小于跨节点的pipeline的。

一般而言，总的GPU数量是一定的。在这种情况下，pipeline占用更多的GPU，就意味着其它“完美并行”（无bubble）的方式会占用更少的GPU，比如DDP与tensor parallel。二者中，DDP的传输可以和backward并行，但tensor parallel不行，所以会更加显著地受到带宽的限制。一个经验性的建议是，应该尽量减少单个进程占据的GPU的数量，但是可以考虑适当增加每个GPU内的pipeline数量。最后，我们再来解释一下Megatron的pipeline。

本质上，pipeline的bubble来自于启动时GPU i 要等待GPU i-1 的计算结果。每个GPU执行的时间越久，等待的时间就越久，bubble也会更大。核心的思路在于，如何减少GPU处理每个stage的时间。一方面，我们可以通过减少micro batch size的大小，这个接下来会有讨论。另一方面，我们可以把stage拆得更细致，让每个stage的执行时间更短。这实际上就是Megatron中提出的pipeline的做法。

这里放一张图帮助理解：

 假设三个颜色分别代表3个micro batch，总的forward时间为18个格子，backward时间为24个格子。

在默认做法中，我们将计算平均分配到三个GPU上，每个GPU分到6个格子，执行完再传给流水线上的下一个GPU。对应上半个示意图。

另一种方式是，我们将计算拆成6份，每个GPU负责 不连续 的两份，以”interleaved”的方式进行分配。这样，GPU i只需要三个单位的时间就能够执行完毕传递给 GPU i + 1。本质上就是让启动时间尽量短。

这样做带来的额外开销是，数据的传输量增加了。假设每个GPU负责 v 个stage，那么传输量就变为了原来的 v 倍。

Megatron论文里的图片把forward和backward拆散了，看起来不那么直观。注意backward和forward是否并行都不会影响pipeline的执行效率，因为GPU已经跑满了（没跑满的话可以参照前面的讨论）。

Megatron拆开forward和backward的目的在于节约显存占用。如果等待forward全部完成后再进行backward，那么全部的micro batch都要被存下来留着backward时用。但是如果拆散forward与backward，可以理解为对于每一个单独的micro batch都尽可能早地完成forward+backward（而不是等待所有forward都完成后再一起backward），完成backward后就不需要再保留micro batch的数据了，所以节约了显存。

如果等待全部forward完成再进行backward的话，需要保存的数据量正比于micro batch的数量 m；如果拆散了的话，需要保存的数据量正比于pipeline的深度 p。考虑到 m≫p，拆散了更好。

Micro Batch Size

 在Megatron上，一个经验性的实验是：

micro batch size	2	4	8
time (s)	4.79	4.43	5.69

Checkpoint Layers

 由于 c的取值理论上并不会影响训练效率，最终不超过显存容量即可。根据Megatron论文中的建议，c取1或2是比较合适的值。

在Megatron上的实验验证了checkpoint的粒度并不会对效率产生显著的影响，浮动约为8%：

checkpoint layers	1	2	4	8
total	4.39	4.43	4.74	4.55

在我们的方法上得到的结果类似，浮动仅为4%：

checkpoint layers	1	2	4	8	16	32
forward	0.60	0.59	0.60	0.60	0.60	0.59
backward	5.64	5.62	5.38	5.38	5.40	5.42
total	6.41	6.37	6.15	6.14	6.16	6.18

Fused Kernels

Megatron的作者提供了一些fused kernels来提高计算效率。通过将bias-gelu和masked-softmax两个fusion，模型能获得约8.5%的提升，单次迭代时间从4.43s提高到4.08s。

总结

1. pipeline优化。pytorch自带的pipeline还是有比较大的改进空间的，尤其是在发生跨numa的时候，与Megatron的实现产生了非常大的差距（而且pytoch的pipe不支持跨节点）。好的pipeline实现是训练大模型必不可少的一部分，可以考虑像hfreduce一样实现一个hfpipe。

2. 关注硬件特性。不同的 (layers, hidden size) 的组合，即使具有相同的理论计算量，实际执行起来的效率差异可以高达85+%。背后的原因应该是矩阵形状的不同。尽管在设计一个模型的时候，训练效率并不是第一考量，但是我们可以通过轻微的调整来追求更高的训练效率。与此同时，另一个可行的做法是通过tensor parallel将矩阵变为最合适的形状。

3. 当硬件架构、带宽已经确定后，tensor parallel能否被高效执行是存疑的。但是依旧可能存在某种专门的实现，使tensor parallel的传输开销能够小于pipeline parallel的bubble开销，来达到Megatron中所宣称的执行效率。

OneFlow的大模型分片保存和加载策略

撰文 | 李响

1、大规模模型分片存储简介

在模型比较小时（如 100G 以下），还有可能采用单机存储。当模型参数量比较大时，要求的样本数也更大，训练后做 dump 出来的模型也会很大，单机肯定放不下。

比如，由 DeepSpeed 和 Megatron 驱动的 Megatron 图灵自然语言生成模型（MT-NLG）具有 5300 亿个参数，是迄今为止训练过的最大和最强大的单片 Transformer 语言模型，支持这样的大规模语言模型需要分片保存和加载，不会使用单机内存。此外，在其他 CV、搜索、推荐和广告类等场景下，读取样本量增多和模型复杂度增加都会带来模型存储上的难题。

本文将介绍 OneFlow 的大模型分片保存、加载策略以及使用方法。

2

OneFlow 模型分片保存和加载

OneFlow 的大模型分片保存和加载的实现基于全局视角（Global View，https://docs.oneflow.org/master/cookies/global_tensor.html）的概念，既利用 Placement 与 SBP 完成模型文件（下文都用 state dict 表示）在各个物理设备上的切分，适用于当模型大到无法在单个设备的内存或显存上容纳下的场景。

flow.utils.global_view.to_global() 接口介绍

为了更好理解下文保存模型和加载模型两个部分的内容，首先对 flow.utils.global_view.to_global() 接口和其实现思路进行分析。

区别于现有的 Tensor.to_global() 模式（可以处理普通的 Tensor，https://oneflow.readthedocs.io/en/master/generated/oneflow.Tensor.to_global.html?highlight=to_global%28%29），提供了多种类型的输入支持，包括 None、Tensor、List、Tuple、nn.Module 的 state dict 、nn.Graph 的 state dict 和几种类型的任意组合，既将 List/Tuple/Dict 中的输入 Tensor 转换为 Global Tensor。值得注意的是，其传入参数中的 SBP 支持用户自定义一个 (x, tensor) -> sbp 的函数来解决不同 Tensor 对应不同 SBP 的需求。

并且，与 to_global() 对应的还有 flow.utils.global_view.to_local() 接口。可以参考 API 文档中关于 to_global() 和 to_local() 更详细的介绍（https://oneflow.readthedocs.io/en/master/utils.global_view.html）。在 flow.utils.global_view.to_global() 的实现（https://github.com/Oneflow-Inc/oneflow/blob/master/python/oneflow/utils/global_view/to_global.py）中，支持了多种输入类型适用于现有的 Tensor.to_global() 接口。实现的整体思路大致为检查输入、广播（空）结构，遍历节点、调用回调函数和返回 to_global() 后的结果。

再回到我们关注的地方，这个接口如何做到模型分片保存和加载？

比如对于模型并行/流水并行，模型的参数分散在多个 Rank 上，在保存模型前通过 flow.utils.global_view.to_global() 将 state dict 里的每个 Tensor 在指定 Placement 上转为 Global Tensor，SBP 的类型为 flow.sbp.split，可以设置在特定维度上的切分。同样的，模型也可以按 Split 被加载。当然，SBP 也可以为 Broadcast，支持不同的 SBP 和 Placement 组合。这样，超大规模模型分片存储的问题就被非常好地解决了。

保存模型

大致了解 flow.utils.global_view.to_global() 接口后，在这一部分演示了如何分片保存模型，代码如下：

# 自定义 get_sbp 函数。
def get_sbp(state_dict, tensor):
    if tensor is state_dict["System-Train-TrainStep"]:
        return flow.sbp.broadcast
    if tensor is state_dict["module_pipeline"]["m_stage3.linear.weight"]:
        return flow.sbp.split(1)
    if tensor is state_dict["module_pipeline"]["m_stage3.linear.bias"]:
        return flow.sbp.broadcast
    return flow.sbp.split(0)


model_file_state_dict = flow.utils.global_view.to_global(
    state_dict, placement=model_file_placement, sbp=get_sbp, 
    ) # 使用 sbp=get_sbp 处理特殊的键，也支持指定普通的 SBP。


rank_id = flow.env.get_rank()
# 保存模型分片的路径，一个 rank 对应一个路径。
state_dict_dir = "./graph_save_load_global_" + str(rank_id)


if flow.env.get_rank() in model_file_placement.ranks:
    flow.save(
        flow.utils.global_view.to_local(model_file_state_dict),
        state_dict_dir,
    )

首先，将原模型（state_dict）转化到模型文件的 Placement 和 SBP 上，model_file_placement 为要分片保存模型的设备阵列，也就是将 state dict 按 split(0) 分片到 model_file_placement 上。

这里之所以自定义 get_sbp 函数，是因为用户可以传进来一个 (x, tensor) -> sbp 的函数来解决特殊 Tensor 对应不同 SBP 的需求。

举个例子(当前例子基于 Graph 模式)，对于 state_dict["System-Train-TrainStep"] 这种 shape 为 [1] 的 Tensor，我们就不能按 split(0) 分片了，SBP 可以选用 broadcast。而 state_dict["module_pipeline"]["m_stage3.linear.weight"] 只能在第 1 维度切分，对于 state_dict["module_pipeline"]["m_stage3.linear.bias"] 这种不可切分的小 Tensor(s)，SBP 可以选用 broadcast。这样支持用户 DIY SBP 的处理，更加灵活。

在后面的处理中，使用 flow.utils.global_view.to_local() 接口得到 model_file_state_dict 的本地分量，并调用 save() 保存模型。其中，state_dict_dir 是带有设备 id 的目录，需要区分不同设备，推荐一个 rank 对应一个路径，路径名用 rank id 的方式。

加载模型

在指定设备上分片保存模型后，加载模型的代码如下：

if cur_rank in model_file_placement.ranks:
    local_state_dict = flow.load(state_dict_dir)
else:
    local_state_dict = None


global_state_dict = flow.utils.global_view.to_global(
     local_state_dict, placement=model_file_placement, sbp=get_sbp,
)
graph_model.load_state_dict(global_state_dict)

首先，用 load() 方法在每个保存切片的设备上加载 state dict。对应的，需要把 local rank 上的 state dict 转换到模型文件的 placement 和 sbp 上，得到了 global_state_dict。这一步和保存模型应该是对应的，SBP 和 Placement 也是一致的。

最后，global_state_dict 可以成功加载到 graph_model（nn.Graph） 中。当然，nn.Module 和 nn.Graph 处理方法是一致的。

将 state dict 加载到 nn.Module 中

除了以上两个特征外，在将 state dict 加载到 nn.Module 时，OneFlow 提供了 SBP 和 Placement 的自动转换。

在下面的例子中，首先构造一个 m（nn.Module）对象，再将 global_state_dict 的 SBP 设置为 split(0)，而 m 的 SBP 为 broadcast。同时 placement 也放生了变化，从 placement("cpu", ranks=[0, 1]) 到 flow.placement("cpu", ranks=[0])。这时用户不需要其他操作，OneFlow 会自动做 SBP 和 placement 的转换过程。

import oneflow as flow


m = flow.nn.Linear(2,6)
model_file_placement = flow.placement("cpu", ranks=[0, 1])


state_dict = "weight":flow.ones(3,2), "bias":flow.zeros(3)
global_state_dict = flow.utils.global_view.to_global(
    state_dict, placement=model_file_placement, sbp=flow.sbp.split(0),
)


m.to_global(placement=flow.placement("cpu", ranks=[0]), sbp=flow.sbp.broadcast)
m.load_state_dict(global_state_dict)
print(m.state_dict())

使用 2 卡运行上面的代码，可以看到，我们自己构造的字典中的全局张量，已经被加载到 m Module 中。此外，输出 OrderedDict 的 tensor 的 SBP 已经从 split(0) 自动转换为 broadcast，'weight' 对应 tensor 的形状也是我们期待的 [6, 2]，'bias' 形状为 [6]。

OrderedDict([('weight', tensor([[1., 1.],
        [1., 1.],
        [1., 1.],
        [1., 1.],
        [1., 1.],
        [1., 1.]], placement=oneflow.placement(type="cpu", ranks=[0]), sbp=(oneflow.sbp.broadcast,), dtype=oneflow.float32,
       requires_grad=True)), ('bias', tensor([0., 0., 0., 0., 0., 0.], placement=oneflow.placement(type="cpu", ranks=[0]), sbp=(oneflow.sbp.broadcast,),
       dtype=oneflow.float32, requires_grad=True))])

3

一个完整示例

上面演示了如何分片保存和加载模型。在这一部分，提供一份完整的代码参考，下面的例子为 4 个 ranks 上的流水并行，模拟了模型分片保存和加载的过程。

import os
import numpy as np


import oneflow as flow


model_tensor_placement = flow.placement("cuda", ranks=[0, 1, 2, 3])
# model_file_placement 为存储模型分片的设备的 placement，表示在 Rank 2 和 Rank 3 上可为 None。
model_file_placement = flow.placement("cpu", ranks=[0, 1])
P0 = flow.placement(model_tensor_placement.type, ranks=[0])
P1 = flow.placement(model_tensor_placement.type, ranks=[1])
P2 = flow.placement(model_tensor_placement.type, ranks=[2])
P3 = flow.placement(model_tensor_placement.type, ranks=[3])


def get_sbp(state_dict, tensor):
    if tensor is state_dict["System-Train-TrainStep"]:
        return flow.sbp.broadcast
    if tensor is state_dict["module_pipeline"]["m_stage3.linear.weight"]:
        return flow.sbp.split(1)
    if tensor is state_dict["module_pipeline"]["m_stage3.linear.bias"]:
        return flow.sbp.broadcast
    return flow.sbp.split(0)


class Stage0Module(flow.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = flow.nn.Linear(16, 8)
        self.relu = flow.nn.ReLU()


    def forward(self, x):
        return self.relu(self.linear(x))


class Stage1Module(flow.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = flow.nn.Linear(8, 4)
        self.relu = flow.nn.ReLU()


    def forward(self, x):
        return self.relu(self.linear(x))


class Stage2Module(flow.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = flow.nn.Linear(4, 2)
        self.relu = flow.nn.ReLU()


    def forward(self, x):
        return self.relu(self.linear(x))


class Stage3Module(flow.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = flow.nn.Linear(2, 1)


    def forward(self, x):
        return self.linear(x)


# 模拟 4 个 ranks 上的流水并行
class PipelineModule(flow.nn.Module):
    def __init__(self):
        super().__init__()
        self.m_stage0 = Stage0Module()
        self.m_stage1 = Stage1Module()
        self.m_stage2 = Stage2Module()
        self.m_stage3 = Stage3Module()


        self.m_stage0.to_global(placement=P0, sbp=flow.sbp.broadcast)
        self.m_stage1.to_global(placement=P1, sbp=flow.sbp.broadcast)
        self.m_stage2.to_global(placement=P2, sbp=flow.sbp.broadcast)
        self.m_stage3.to_global(placement=P3, sbp=flow.sbp.broadcast)


    def forward(self, x):
        out_stage0 = self.m_stage0(x)


        in_stage1 = out_stage0.to_global(placement=P1, sbp=flow.sbp.broadcast)
        out_stage1 = self.m_stage1(in_stage1)


        in_stage2 = out_stage1.to_global(placement=P2, sbp=flow.sbp.broadcast)
        out_stage2 = self.m_stage2(in_stage2)


        in_stage3 = out_stage2.to_global(placement=P3, sbp=flow.sbp.broadcast)
        out_stage3 = self.m_stage3(in_stage3)


        return out_stage3


class PipelineGraph(flow.nn.Graph):
    def __init__(self, module_pipeline):
        super().__init__()
        self.module_pipeline = module_pipeline
        self.module_pipeline.m_stage0.config.set_stage(0, P0)
        self.module_pipeline.m_stage1.config.set_stage(1, P1)
        self.module_pipeline.m_stage2.config.set_stage(2, P2)
        self.module_pipeline.m_stage3.config.set_stage(3, P3)
        self.config.set_gradient_accumulation_steps(2)
        self.add_optimizer(
            flow.optim.SGD(self.module_pipeline.parameters(), lr=0.001)
        )


    def build(self, x):
        out = self.module_pipeline(x)
        out = out.sum()
        out.backward()
        return out


def train_with_graph(call_cnt=0, state_dict_dir=None, last_state_dict=None):
    # 形状为 [2, 16] 的固定输入张量
    x = flow.tensor(
        [
            [
                0.4286,
                0.7402,
                0.4161,
                0.6103,
                0.7394,
                1.1330,
                -0.2311,
                -0.1013,
                0.8537,
                0.9757,
                -0.9842,
                0.3839,
                -0.5551,
                -0.8832,
                0.7820,
                0.7421,
            ],
            [
                -0.1581,
                -1.0319,
                1.8430,
                0.3576,
                0.7288,
                -0.6912,
                0.9966,
                1.0840,
                -1.1760,
                1.5683,
                -0.2098,
                -1.6439,
                -2.7049,
                0.1949,
                1.6377,
                0.0745,
            ],
        ],
        dtype=flow.float32,
        placement=P0,
        sbp=flow.sbp.broadcast,
    )


    module_pipeline = PipelineModule()
    graph_model = PipelineGraph(module_pipeline)
    cur_rank = flow.env.get_rank()


    if call_cnt == 1:
        if cur_rank in model_file_placement.ranks:
            local_state_dict = flow.load(state_dict_dir)
        else:
            local_state_dict = None


        # 使用 sbp=get_sbp 处理特殊的键
        global_state_dict = flow.utils.global_view.to_global(
            local_state_dict, placement=model_file_placement, sbp=get_sbp,
        )
        graph_model.load_state_dict(global_state_dict)


    graph_model(x)
    state_dict = graph_model.state_dict()


    if call_cnt == 0:
        model_file_state_dict = flow.utils.global_view.to_global(
            state_dict, placement=model_file_placement, sbp=get_sbp,
        )
        if flow.env.get_rank() in model_file_placement.ranks:
            flow.save(
                flow.utils.global_view.to_local(model_file_state_dict),
                state_dict_dir,
            )


if __name__=="__main__":
    rank_id = flow.env.get_rank()
    # 保存路径，一个 rank 对应一个路径。
    state_dict_dir = "./graph_save_load_global_" + str(rank_id)
    # 保存模型
    train_with_graph(0, state_dict_dir)
    # 加载模型
    train_with_graph(1, state_dict_dir)

4

结语

本文从简单介绍大规模模型分片存储开始，最终演示了 OneFlow 的如何做模型分片保存和加载的过程，后续 OneFlow 的大模型分片存储的接口还会不断完善。

其他人都在看

• OneFlow v0.8.0正式发布

• 深度学习硬件的过去、现在和未来

• Cerebras：世界上最大AI芯片的架构设计

• Groq：从头设计一个张量流式处理器架构

• CUDA入门教程；Transformer太火不是好事？

• OneEmbedding:单卡训练TB级推荐模型不是梦

• 大模型训练难？效率超群、易用的“李白”模型库来了

欢迎体验OneFlow v0.8.0：GitHub - Oneflow-Inc/oneflow: OneFlow is a deep learning framework designed to be user-friendly, scalable and efficient.OneFlow is a deep learning framework designed to be user-friendly, scalable and efficient. - GitHub - Oneflow-Inc/oneflow: OneFlow is a deep learning framework designed to be user-friendly, scalable and efficient.https://github.com/Oneflow-Inc/oneflow/