sklearn实现逻辑回归_以python为工具Python机器学习系列

Posted 2022-08-22 侯小啾

sklearn实现逻辑回归_以python为工具【Python机器学习系列（十）】

文章目录

• 1.线性逻辑回归
• 2.非线性逻辑回归
• 3.乳腺癌数据集案例

---

      ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ
                 
    ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ

---

大家好，我是侯小啾！

 今天分享的内容是，通过python的sklearn库实现线性逻辑回归和非线性逻辑回归。
  

---

1.线性逻辑回归

第一步，读取并提取数据：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression

# 读取数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:, :-1]
y_data = data[:, -1]

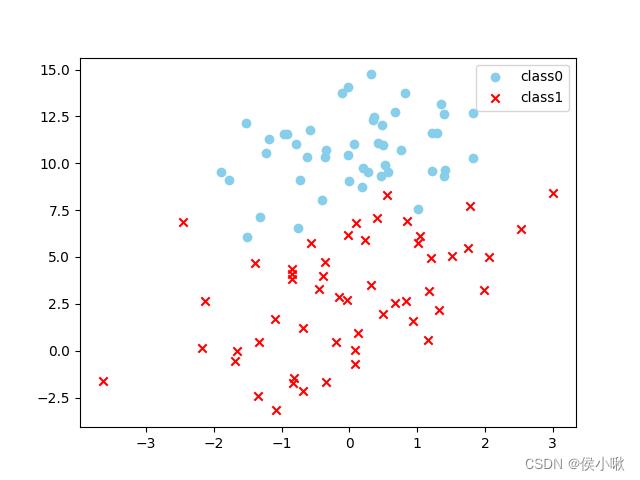
然后定义绘制散点图的函数，为将数据分布更直观地展示：

def plot_logi():
    # 初始化列表
    x_0 = []
    y_0 = []
    x_1 = []
    y_1 = []
    # 分割不同类别的数据
    for i in range(len(x_data)):
        # 取类别为0的数据
        if y_data[i] == 0:
            # 将特征1添加到x_0中
            x_0.append(x_data[i, 0])
            # 将特征2添加到y_0中
            y_0.append(x_data[i, 1])
        else:
            # 将特征1添加到x_1中
            x_1.append(x_data[i, 0])
            # 将特征2添加到y_1中
            y_1.append(x_data[i, 1])

    # 画图
    plt.scatter(x_0, y_0, c="skyblue", marker="o", label="class0")
    plt.scatter(x_1, y_1, c="red", marker="x", label="class1")
    plt.legend()

输出数据分布散点图：

plot_logi()
plt.show()

      

---

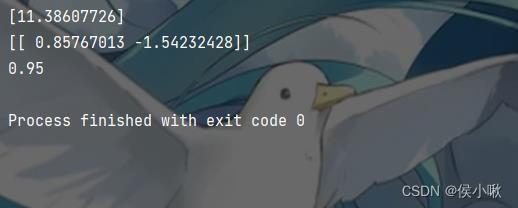
第三步，训练模型

logistic = LogisticRegression()
logistic.fit(x_data, y_data)

# 截距
print(logistic.intercept_)
# 系数：theta1 theta2
print(logistic.coef_)
# 预测
pred = logistic.predict(x_data)
# 输出评分
score = logistic.score(x_data, y_data)
print(score)

输出结果如下图所示：
        

---

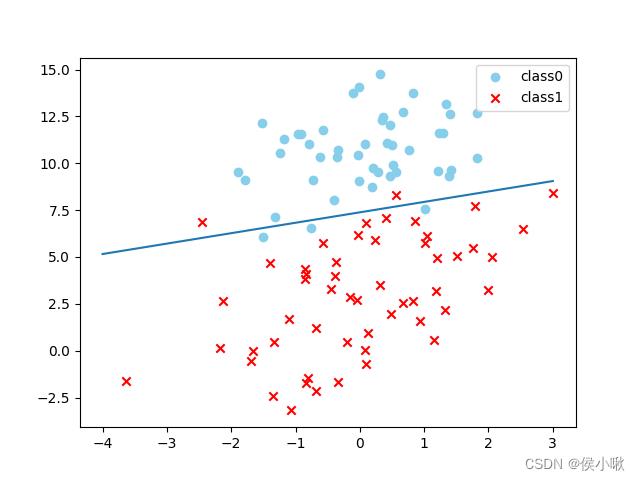
绘制出带有决策边界的散点图：

# 绘制散点
plot_logi()
# 绘制决策边界
x_test = np.array([[-4], [3]])
y_test = -(x_test*logistic.coef_[0, 0]+logistic.intercept_)/logistic.coef_[0, 1]
plt.plot(x_test, y_test)
plt.show()

        

---

2.非线性逻辑回归

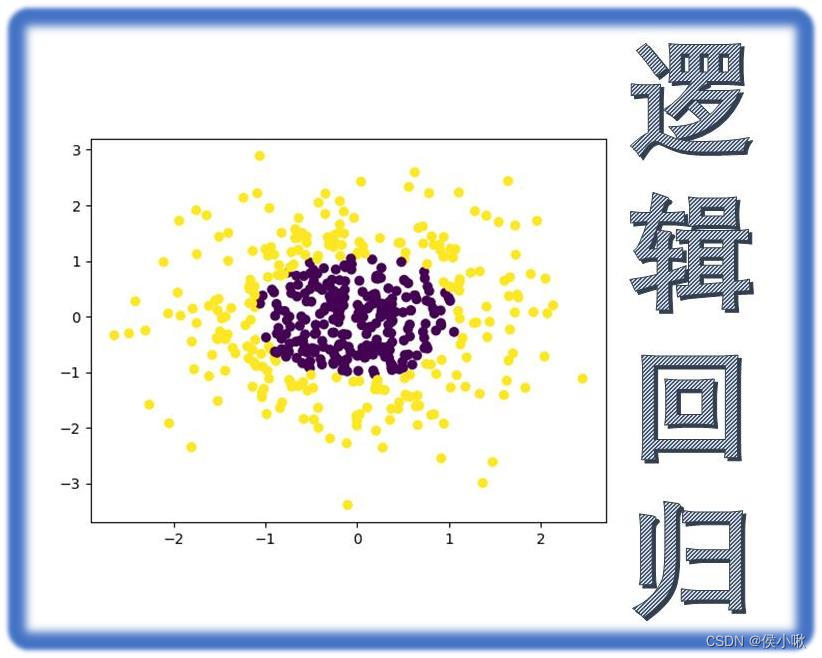
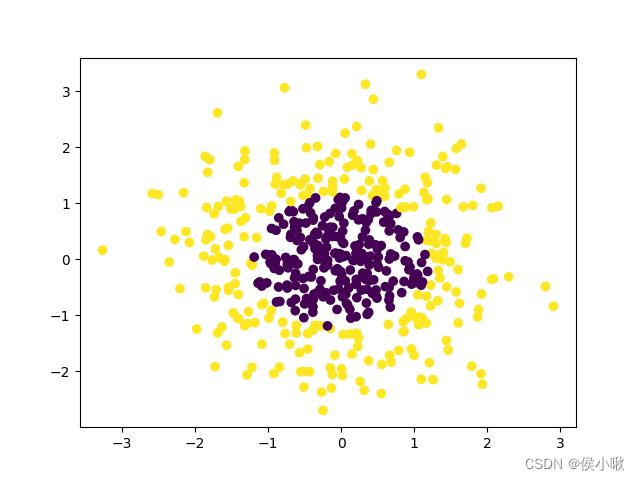
python实现非线性逻辑回归，首先使用make_gaussian_quantiles获取一组高斯分布的数据集，代码及数据分布如下：

import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.datasets import make_gaussian_quantiles


# 获取高斯分布的数据集，500个样本，2个特征，2分类
x_data, y_data = make_gaussian_quantiles(n_samples=500, n_features=2, n_classes=2)
# 绘制散点图
plt.scatter(x_data[:, 0], x_data[:, 1],c=y_data)
plt.show()

描述数据分布的散点图如图所示：
        

---

然后转换数据并训练模型以实现非线性逻辑回归：

# 数据转换，最高次项为五次项
poly_reg = PolynomialFeatures(degree=5)
x_poly = poly_reg.fit_transform(x_data)


# 定义逻辑回归模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_poly, y_data)
score = logistic.score(x_poly, y_data)
print(score)

评分结果如图所示，达0.996：
        

---

3.乳腺癌数据集案例

以乳腺癌数据集为例，建立线性逻辑回归模型，并输出准确率，精确率，召回率三大指标，代码如下所示：

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
import warnings

warnings.filterwarnings("ignore")

# 获取数据
cancer = load_breast_cancer()
# 分割数据
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.2)

# 创建估计器
model = LogisticRegression()
# 训练
model.fit(X_train, y_train)

# 训练集准确率
train_score = model.score(X_train, y_train)
# 测试集准确率
test_score = model.score(X_test, y_test)
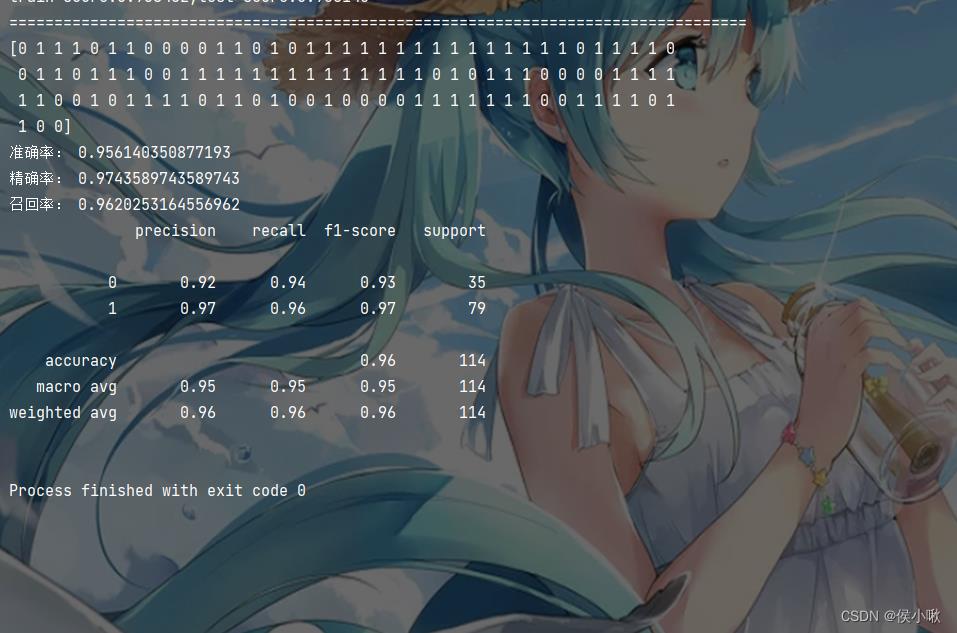
print('train score:train_score:.6f;test score:test_score:.6f'.format(train_score=train_score, test_score=test_score))
print("==================================================================================")
# 再对X_test进行预测
y_pred = model.predict(X_test)
print(y_pred)
# 准确率 所有的判断中有多少判断正确的
accuracy_score_value = accuracy_score(y_test, y_pred)
# 精确率 预测为正的样本中有多少是对的
precision_score_value = precision_score(y_test, y_pred)
# 召回率 样本中有多少正样本被预测正确了
recall_score_value = recall_score(y_test, y_pred)

print("准确率：", accuracy_score_value)
print("精确率：", precision_score_value)
print("召回率：", recall_score_value)

# 输出报告模型评估报告
classification_report_value = classification_report(y_test, y_pred)

print(classification_report_value)

程序输出结果如下图所示：

---

本次分享就到这里，小啾感谢您的关注与支持！
🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ

本专栏更多好文欢迎点击下方连接：
 
1.初识机器学习前导内容_你需要知道的基本概念罗列_以PY为工具 【Python机器学习系列（一）】
 
2.sklearn库数据标准预处理合集_【Python机器学习系列（二）】
 
3.K_近邻算法_分类Ionosphere电离层数据【python机器学习系列（三）】
 
4.python机器学习 一元线性回归 梯度下降法的实现 【Python机器学习系列（四）】
 
5.sklearn实现一元线性回归 【Python机器学习系列（五）】
 
6.多元线性回归_梯度下降法实现【Python机器学习系列（六）】
 
7.sklearn实现多元线性回归 【Python机器学习系列（七）】
 
8.sklearn实现多项式线性回归_一元/多元 【Python机器学习系列（八）】
 
9.逻辑回归原理梳理_以python为工具 【Python机器学习系列（九）】